文章目录
- 1. JZ83 剪绳子(进阶版)
- 2. JZ18 删除链表的节点
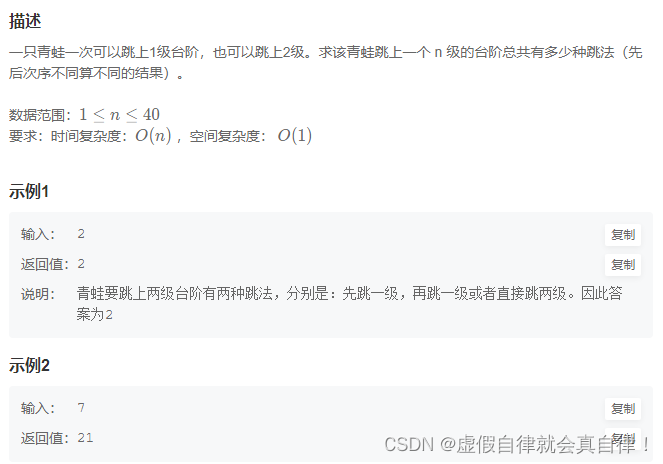
- 3. JZ69 跳台阶
- 4. JZ44 数字序列中某一位的数字
- 5. JZ11 旋转数组的最小数字
- 6. JZ56 数组中只出现一次的两个数字
- 统计频率
- 位运算
- 7. JZ85 连续子数组的最大和(二)
- 8. JZ84 二叉树中和为某一值的路径(三)
- 两次dfs
- 一次dfs+哈希表
- 9. JZ86 在二叉树中找到两个节点的最近公共祖先
- 10. JZ68 二叉搜索树的最近公共祖先
1. JZ83 剪绳子(进阶版)
只能分成2和3,暴力乘法会超时
class Solution {
public:
long long cutRope(long long number) {
if(number < 2) return 0;
if(number < 4) return number-1;
//暴力乘方 超时
long long result = 1, mod = 998244353;
//只能分成 2 3 要对998244353 取模
while(number > 4)
{
result *= 3;
result %= mod;
number -= 3;
}
result *= number;
result %= mod;
return result;
}
};

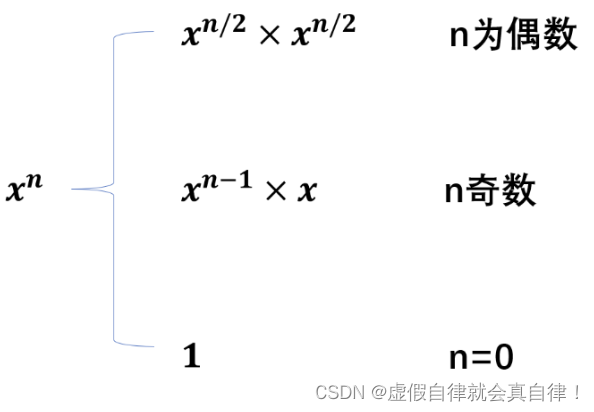

3个数越多答案越大,所以n%3有三种情况:
- 余数为0直接做3^(n/3)
- 余数为1做4*3^((n-4)/3)
- 余数为2做2*3^((n-2)/3)
2. JZ18 删除链表的节点

/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
ListNode* deleteNode(ListNode* head, int val) {
if(head == nullptr) return nullptr;
//写法1
ListNode* fast = head;//找到删除节点
ListNode* dummyhead = new ListNode(0);
ListNode* slow = dummyhead;//断开连接
dummyhead->next = head;
while(fast)
{
if(fast->val == val)
{
slow->next = fast->next;
break;
}
fast = fast->next;
slow = slow->next;
}
return dummyhead->next;
}
};
- 写法2
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
ListNode* deleteNode(ListNode* head, int val) {
if(head == nullptr) return nullptr;
//写法2
ListNode* dummyhead = new ListNode(0);
dummyhead->next = head;
ListNode* fast = dummyhead;
while(fast->next)
{
if(fast->next->val == val)
{
fast->next = fast->next->next;
break;
}
fast = fast->next;
}
return dummyhead->next;
}
};
3. JZ69 跳台阶
class Solution {
public:
int jumpFloor(int number) {
if(number <= 2) return number;
int fistjump = 1;
int secondjump = 2;
int res = 0;
for(int i=3; i<=number; i++)
{
res = fistjump + secondjump;
fistjump = secondjump;
secondjump = res;
}
return res;
}
};
4. JZ44 数字序列中某一位的数字

#include <string>
class Solution {
public:
int findNthDigit(int n) {
if(n <= 9) return n;
/*
小于10的数字一位数,1~9,共9个数字,9位 1位数 区间是 1~9 起点是1 9个数字 9位;
小于100的数字两位数,10~99,共90个数字,180位 2位数 区间是 10~99 起点是10 90个数字 180位;
小于1000的数字三位数,100~999,共900个数字,2700位 3位数 区间是 100~999 起点是100 900个数字 2700位;
*/
int digit = 1; // n是几位数
long long start = 1; // 当前位数 所在的区间
long long total = 9; // 当前区间 之前总共有多少位数字
while(n > total) //不是1位数
{
n -= total;
digit++;
start *= 10;
total = 9 * digit * start;//每个数字digit位
}
int num = start + (n-1) / digit;//定位n在哪个区间
int index = (n-1) % digit;//定位n在该区间的哪一位 也就是往后偏移
return to_string(num)[index] - '0';
}
};
5. JZ11 旋转数组的最小数字

#include <climits>
class Solution {
public:
int minNumberInRotateArray(vector<int>& nums) {
if(nums.size() <= 0) return 0;
int left=0, right=nums.size()-1;
while(left <= right)
{
int mid = left + (right - left) / 2;
if(nums[mid] > nums[right])//右边是降序 最小的数字在mid右边
left = mid+1;
else if(nums[mid] < nums[right])//右边是升序 最小数字要么是mid(奇数个数字) 要么在mid左边(偶数个)
right = mid;
else right--;//无法判断,一个一个试
}
return nums[left];
}
};
6. JZ56 数组中只出现一次的两个数字

统计频率
#include <algorithm>
class Solution {
public:
vector<int> FindNumsAppearOnce(vector<int>& nums) {
int len = nums.size(), index=0;
vector<int> result;
unordered_map<int, int> hashmap;
for(auto n : nums)
{
hashmap[n]++;
}
auto beg = nums.begin();
auto end = nums.end();
while(beg != nums.end())
{
if(hashmap[*beg] == 1)
{
result.push_back(*beg);
break;
}
beg++;
}
while(end != nums.begin())
{
if(hashmap[*end] == 1)
{
result.push_back(*end);
break;
}
end--;
}
if(result[0] > result[1]) swap(result[0], result[1]);
return result;
}
};
位运算
#include <algorithm>
class Solution {
public:
vector<int> FindNumsAppearOnce(vector<int>& nums) {
int len = nums.size(), index=0;
vector<int> result(2, 0);
//位运算
// 先将全部数进行异或运算,得出得到a^b
int tmp = 0;
for(int n : nums)
tmp ^= n;
//找到两个数不相同的第一位 从最低位开始找起
int mask = 1;
while((mask & tmp) == 0)
mask <<= 1;
//遍历数组,对每个数分类
for(int i=0; i<nums.size(); i++)
{
if((mask & nums[i]) == 0) result[0] ^= nums[i];
else result[1] ^= nums[i];
}
//整理次序
if(result[0] > result[1]) swap(result[0], result[1]);
return result;
}
};
7. JZ85 连续子数组的最大和(二)


class Solution {
public:
vector<int> FindGreatestSumOfSubArray(vector<int>& array) {
vector<int> result;
//滑动区间
int left = 0, right = 0;
//记录最长的区间
int resl = 0, resr = 0;
int last_sum = array[0], now_sum = 0, maxsum = last_sum;
for(int i=1; i<array.size(); i++)
{
right++;
//状态转移:连续子数组和最大值
now_sum = max(array[i], last_sum + array[i]);
//区间新起点
if(last_sum + array[i] < array[i])
left = right;
//更新最大值
if(now_sum > maxsum || now_sum == maxsum && (right - left + 1) > (resr - resl + 1))
{
maxsum = now_sum;
resl = left;
resr = right;
}
//更新x的状态
last_sum = now_sum;
}
//取数组
for(int i = resl; i <= resr; i++)
result.push_back(array[i]);
return result;
}
};
dp写法
class Solution {
public:
vector<int> FindGreatestSumOfSubArray(vector<int>& array) {
vector<int> result;
//滑动区间
int left = 0, right = 0;
//记录最长的区间
int resl = 0, resr = 0;
//dp 写法2
vector<int> dp(array.size(), 0);
dp[0] = array[0];
int maxnum = dp[0];
for(int i=1; i<array.size(); i++)
{
right++;
//状态转移:连续子数组和最大值
dp[i] = max(dp[i-1] + array[i], array[i]);
//区间新起点
if(dp[i-1] + array[i] < array[i])
left = right;
//更新最大值
if(dp[i] > maxnum || dp[i] == maxnum && (right - left + 1) > (resr - resl + 1))
{
maxnum = dp[i];
resl = left;
resr = right;
}
}
//取数组
for(int i = resl; i <= resr; i++)
result.push_back(array[i]);
return result;
}
};
8. JZ84 二叉树中和为某一值的路径(三)
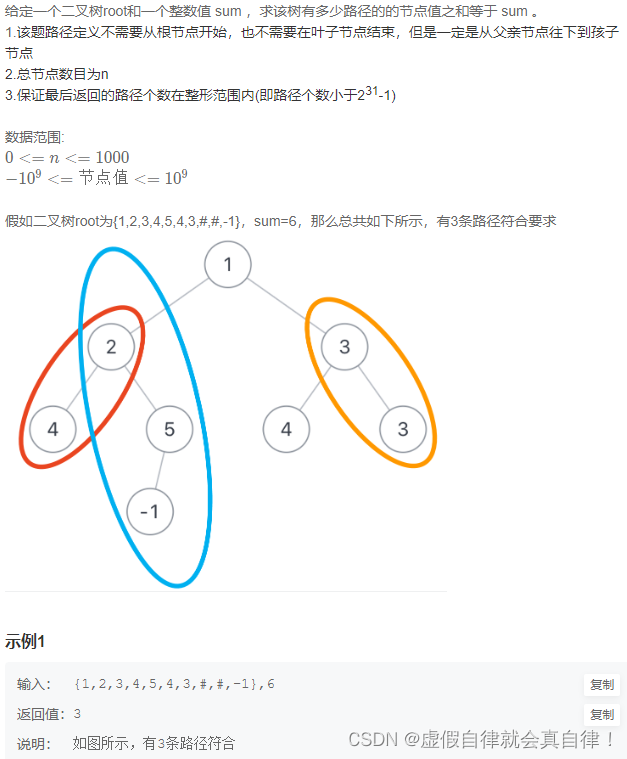
这个题特殊在每一个结点都可能是起始结点。
两次dfs

/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
int count=0;
int FindPath(TreeNode* root, int sum) {
if(root==nullptr) return count;
dfs(root, sum); //查询以某节点为根的路径数
FindPath(root->left, sum); //以其子节点为新根
FindPath(root->right, sum); //以其子节点为新根
return count;
}
//根节点作为起始节点
void dfs(TreeNode* root, int sum)
{
if(root == nullptr) return;
if(sum == root->val) //符合目标值
count++;
//进入子节点继续找
dfs(root->left, sum - root->val);
dfs(root->right, sum - root->val);
}
};
一次dfs+哈希表

哈希表存的是根节点到某一结点的 路径和 与 路径数,然后从该结点开始遍历其子树,累加遍历的结点值temp(相当于路径的后半段),如果temp-sum在哈希表里出现过,就说明这条路径符合要求。不是很会
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <unordered_map>
class Solution {
public:
//记录路径和 及 路径条数
unordered_map<int, int> hashmap;
int FindPath(TreeNode* root, int sum) {
//一次dfs+哈希
//路径和为0的有1条
hashmap[0] = 1;
return dfs2(root, sum, 0);
}
//一次dfs+哈希
int dfs2(TreeNode* root, int sum, int lastsum)
{
//
if(root == nullptr) return 0;
int result =0;
//到目前结点为止的累加和
int temp = root->val + lastsum;
//如果该累加和减去sum在哈希表中出现过,相当于减去前面的分支
if(hashmap.find(temp - sum) != hashmap.end())
//加上有的路径数
result += hashmap[temp - sum];
//增加该次路径和
hashmap[temp]++;
//进入子结点
result += dfs2(root->left, sum, temp);
result += dfs2(root->right, sum, temp);
//回退该路径和,因为别的树枝不需要这边存的路径和
hashmap[temp]--;
return result;
}
};
9. JZ86 在二叉树中找到两个节点的最近公共祖先
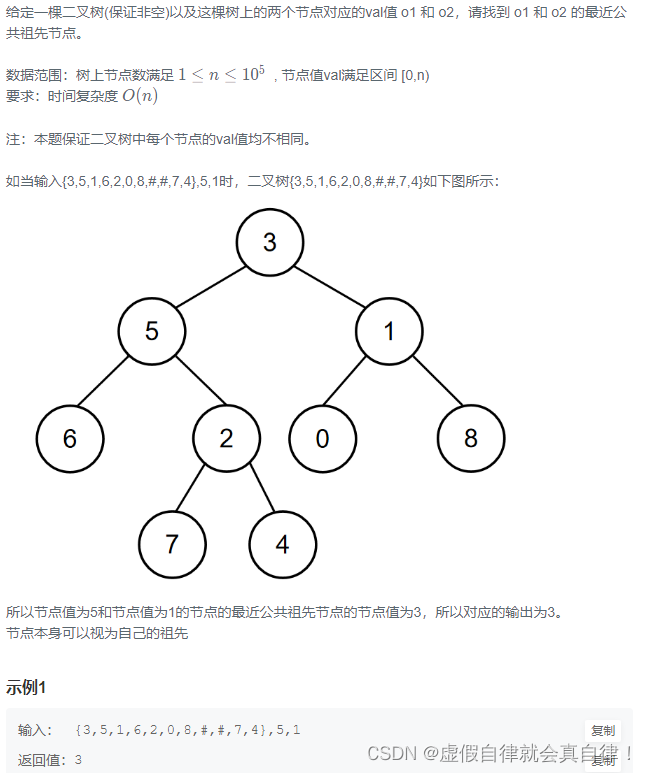
两种情况,一是左子树出现结点p(q),右子树出现节点q(p),那么该节点就是节点p和q的最近公共祖先,如7、4最近公共祖先是2;二是节点本身p(q),它拥有一个子孙节点q§,如5、6最近公共祖先是5。

/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
return dfs(root, o1, o2)->val;
}
TreeNode* dfs(TreeNode* root, int o1, int o2)
{
if(root == nullptr || root->val == o1 || root->val == o2)
return root;
TreeNode* left = dfs(root->left, o1, o2);
TreeNode* right = dfs(root->right, o1, o2);
if(left == nullptr) return right;
if(right == nullptr) return left;
return root;
}
};
10. JZ68 二叉搜索树的最近公共祖先
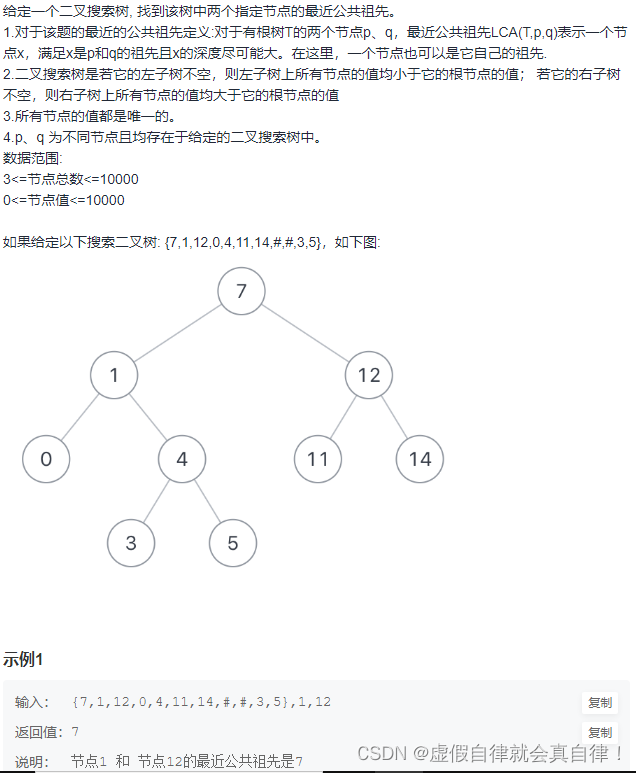
- 因为是有序树,所有 如果 中间节点是 q 和 p 的公共祖先,那么 中节点的数组 一定是在 [p, q]区间的。即 中节点 > p && 中节点 < q 或者 中节点 > q && 中节点 < p。
- 和二叉树的公共祖先不一样的是,从上往下找,因为要找最近的公共祖先,如图
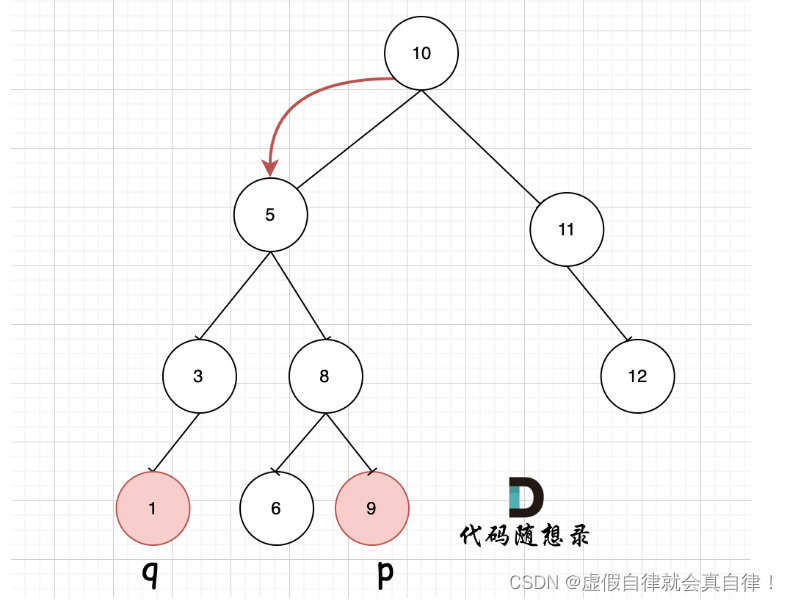
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为q的祖先, 如果从节点5继续向右遍历则错过成为p的祖先。
所以当我们从上向下去递归遍历,第一次遇到 root 节点是数值在[p, q]区间中,那么root 就是 p和q的最近公共祖先。
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
int lowestCommonAncestor(TreeNode* root, int p, int q) {
//空树找不到公共祖先
if(root == nullptr) return -1;
//pq在该节点两边说明这就是最近公共祖先
if((p >= root->val && q <= root->val) || (p <= root->val && q >= root->val))
return root->val;
// 最近公共祖先在左子树
else if(root->val > p && root->val > q)
return lowestCommonAncestor(root->left, p, q);
// 最近公共祖先在右子树
else
return lowestCommonAncestor(root->right, p, q);
}
};




![[oneAPI] 手写数字识别-BiLSTM](https://img-blog.csdnimg.cn/2c9eb12082384d289927663a38f942d0.png)
![[obs] 编译记录](https://img-blog.csdnimg.cn/691b43a100994e829318a2a5dd99ad0e.png)