MCTS 搜索可能的移动并将结果记录在搜索树中。随着执行的搜索次数越多，树及其信息也会变大。为了在Alpha-Go Zero中移动，将计算1，600次搜索。然后构建本地策略。最后，我们从此策略中抽样以采取下一步行动。

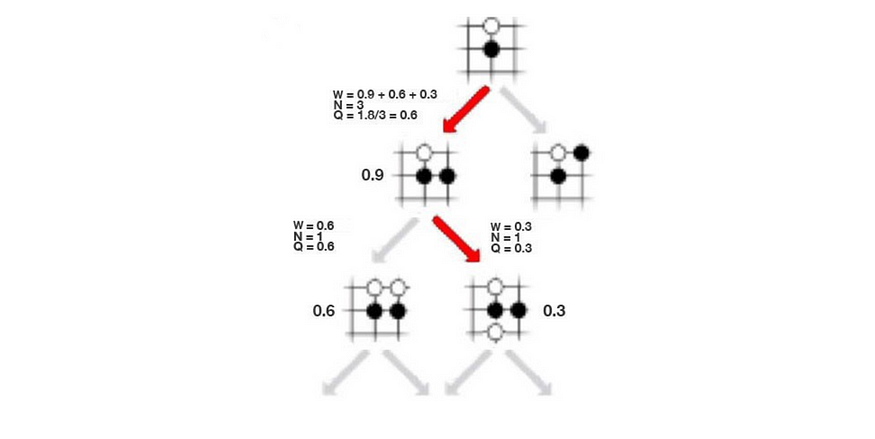
二、MCTS 基本知识

        在此示例中，当前电路板位置为 s₃。

        在 MCTS 中，节点表示电路板位置，边缘表示移动。

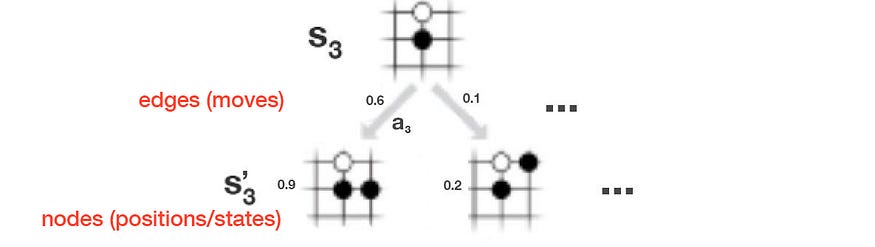
        对于给定的位置，我们可以计算：

• the policy p (p is a probability distribution scoring each action), and
• the value function v (how likely to win at a board position).

        using a deep network f.

        In the example below, it applies a deep network f, composed of convolutional layers, on s₃’ to compute the policy p, and the value function v.

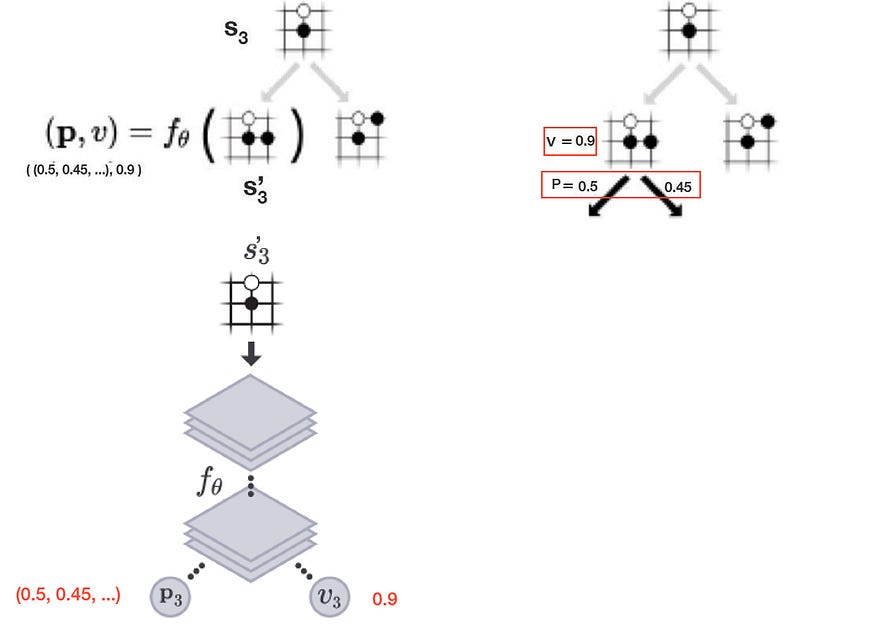
        我们可以通过模拟移动来扩展搜索树。这会将相应的移动添加为边，并将新板位置作为节点添加到搜索树中。

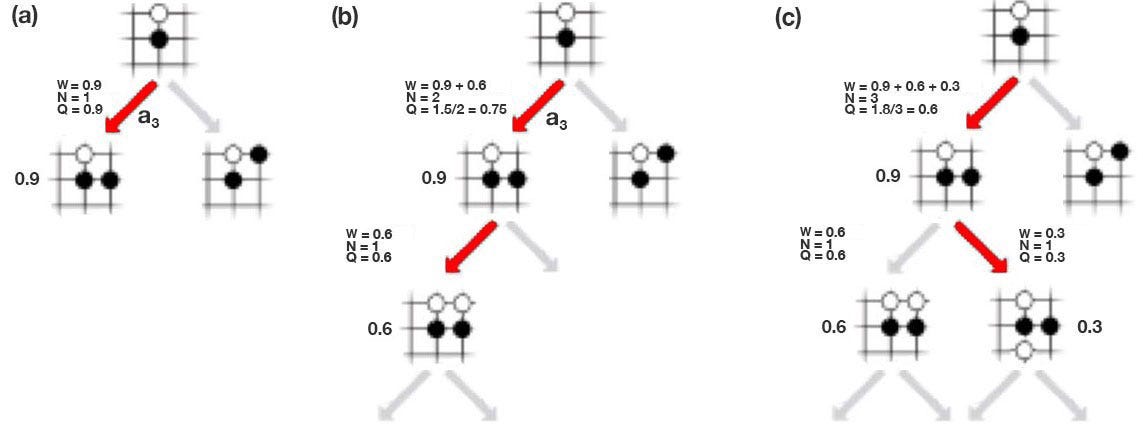
        让我们引入另一个称为操作-值函数 Q 的术语。它衡量给定状态的移动的价值。在下面的（a）中，它以红色移动，f预测获胜几率为0.9。所以 是 0.9。在（b）中，它再移动一次，最终获胜几率为0.6。现在，移动 a₃ 被访问两次，因此我们将访问计数=2。Q 值只是先前结果的平均值，即 W=（0.9+0.6），Q = W/2=0.75。 在（c）中，它探索了另一条道路。现在，a₃ 被访问 3 次， 值为 （0.9+0.6+0.3）/3 = 0.6。

        在 MCTS 中，我们使用 s₃ 作为根逐渐构建搜索树。我们一次添加一个节点，最终在 1.6K 搜索之后，我们使用树为下一步构建本地策略 （π₃）。但是 Go 的搜索空间很大，我们需要优先考虑添加哪个节点并首先搜索。

        需要考虑两个因素：开发和勘探。

• 利用：执行更多看起来有希望的搜索（即高 Q 值）。
• 探索：执行我们不太了解的搜索（即低访问次数 N）。

        在数学上，它根据以下条件选择移动 a：

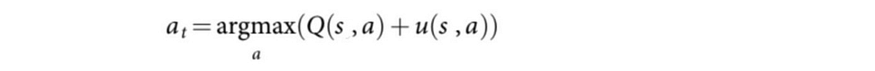
        Q控制开发，u，探索加成，控制探索。

        对于经常访问或不太可能发生的状态-操作对，我们没有动力去更多地探索它。从根开始，它使用此树策略来选择接下来要搜索的路径。

        一开始，MCTS 将更多地关注探索，但随着迭代的增加，大多数搜索都是利用，Q 变得越来越准确。

        AlphaGo Zero迭代上述步骤1，600次以扩展树。

        令人惊讶的是，它不使用 Q 来构建本地策略 π₃。相反，π₃ 是从访问计数 N 派生的。

        在初始迭代之后，将更频繁地访问具有较高 Q 值的移动。它使用访问计数来计算策略，因为它不太容易出现大纲。τ是控制勘探水平的温度。当 τ 为 1 时，它会根据访问计数选择移动。当 τ → 0 时，将仅选取计数最高的移动。所以 τ =1 允许探索，而 τ → 0 不允许。

通过董事会职位，MCTS 计算出更准确的政策π以决定下一步行动。

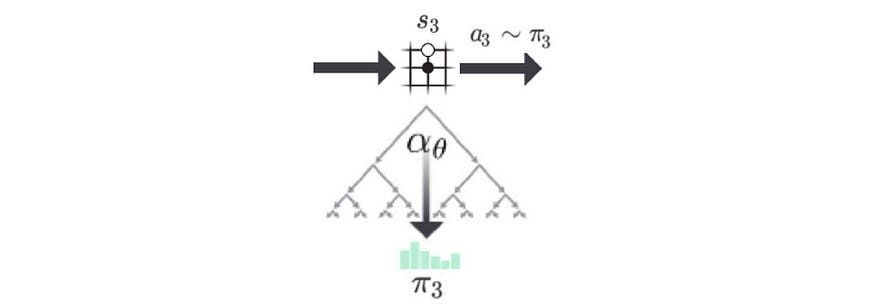
        MCTS改进了政策评估，它使用新的评估来改进政策（政策改进）。然后，它会重新应用策略以再次评估策略。这些策略评估和策略改进的重复迭代在RL中称为策略迭代。在自己玩了很多游戏之后，无论是政策评估还是政策改进都会优化到可以打败高手的程度。有关详细信息，请参阅本文，特别是有关如何训练 f 的信息。

三、MCTS原理

        在详细介绍之前，以下是 MCTS 中的 4 个主要步骤。如图所示，我们将从电路板位置 s₃ 开始。

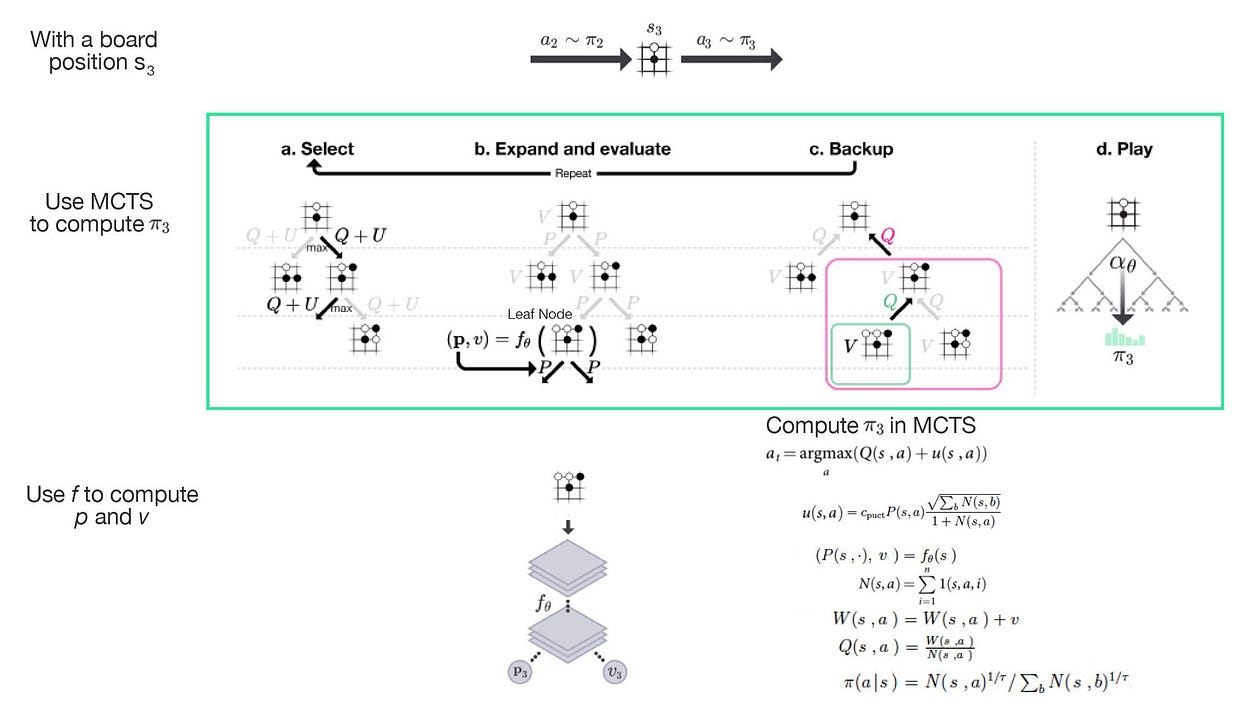
• 步骤 （a） 选择要进一步搜索的路径（移动序列）。从根节点开始，它会搜索在梳理 Q 值 （Q =W/N） 方面具有最高值的下一个操作，以及与访问计数 N 产生不利影响的探索奖励。搜索将继续，直到到达未附加节点的操作。

• 步骤 （b） 通过添加与路径中最后一个操作关联的状态（节点）来扩展搜索树。我们为与新节点关联的操作添加新边，并为每个边记录由 f 计算的 p。
• 步骤 （c） 向后更新 W 和 N 上的当前路径。

重复步骤 （a） 到 （c） 1，600 次后，我们使用访问计数 N 创建新策略 π₃。 我们从此策略中抽样以确定 s₃ 的下一步行动。

接下来，我们将详细介绍每个步骤。

选择

第一步是从树中选择一个路径以进行进一步搜索。假设我们的搜索树如下所示。

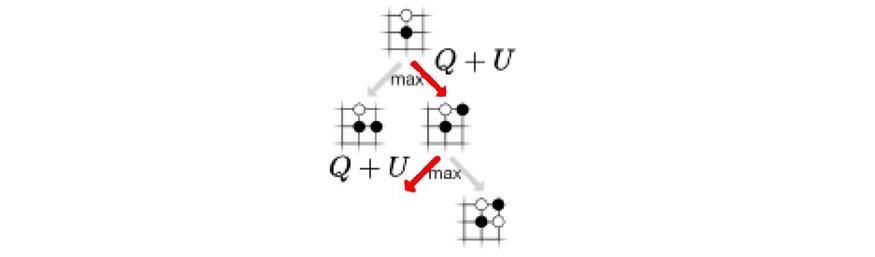
它从根开始，我们根据以下等式选择移动：

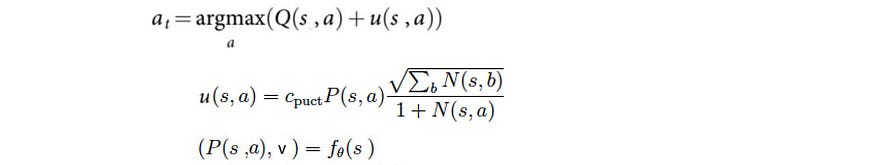
        其中 u 控制探索。它取决于 N 个访问计数，P（s， a） 来自 f 的策略，关于我们为状态 s 选择 a 的可能性，以及 c 一个控制探索级别的超参数。直观地说，探索边缘的频率越低，我们获得的信息就越少，因此我们探索它的奖励就越高。Q 控制开发，这是计算的 Q 值函数 （W/N）。

四、扩展和评估

        确定所选路径后，叶节点将添加到相应操作的搜索树中。它使用深度网络 f 从添加的节点计算策略 p 和 v。

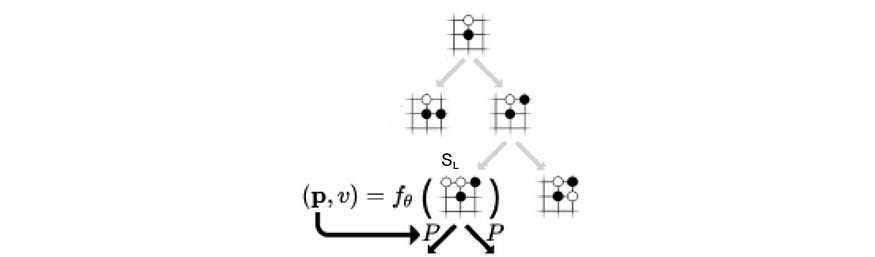
        然后，对于新节点上的每个可能操作，我们添加一个新边 （s， a）。我们将访问计数 N、W 和 Q 初始化为每条边 0。我们记录相应的 v 和 p。

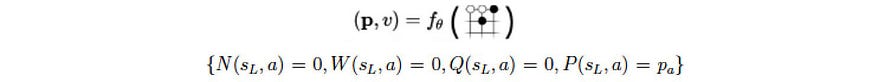
备份

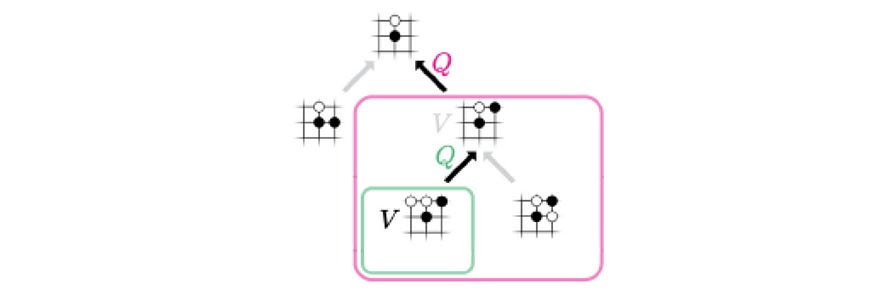
一旦为叶节点计算了 p 和 v，我们备份 v 以更新所选路径中每条边 （s， a） 的操作值 Q。

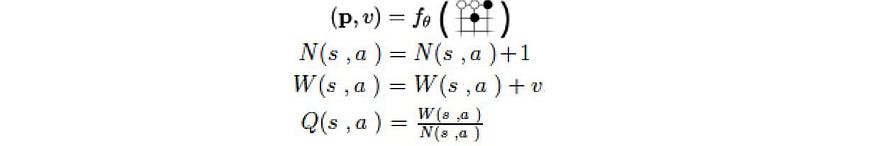
玩

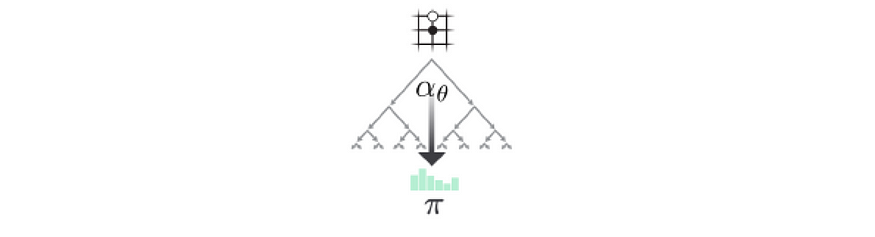
        为了决定下一步行动，AlphaGo Zero根据s₃的每个子级的访问次数创建一个新的本地策略（π₃）。 然后，它从此策略中抽取样本以供下一步操作。

        选定的移动 a 将成为搜索树的根，其所有子项将保留，而其他子项将被丢弃。然后它再次重复 MCTS 以进行下一步操作。