❓剑指 Offer 53 - I. 在排序数组中查找数字 I
难度:简单
统计一个数字在排序数组中出现的次数。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: 2
示例 2:
输入: nums = [5,7,7,8,8,10], target = 6
输出: 0
提示:
- 0 < = n u m s . l e n g t h < = 1 0 5 0 <= nums.length <= 10^5 0<=nums.length<=105
- − 1 0 9 < = n u m s [ i ] < = 1 0 9 -10^9 <= nums[i] <= 10^9 −109<=nums[i]<=109
nums是一个非递减数组- − 1 0 9 < = t a r g e t < = 1 0 9 -10^9 <= target <= 10^9 −109<=target<=109
注意:本题与 34. 在排序数组中查找元素的第一个和最后一个位置 相同(仅返回值不同)。
💡思路:二分查找
只要能找出给定的数字 target 在有序数组第一个位置和最后一个位置,就能知道该数字出现的次数。
- 先考虑如何实现寻找数字在有序数组的第一个位置。正常的二分查找如下,在查找到给定元素
target之后,立即返回当前索引下标。- 但是在查找第一个位置时,找到元素之后应该继续往前找。也就是当
nums[m] >= target时,在左区间继续查找,左区间应该包含target位置。
- 但是在查找第一个位置时,找到元素之后应该继续往前找。也就是当
- 查找最后一个位置可以转换成寻找
target + 1的第一个位置,并再往前移动一个位置。
需要注意以上实现的查找第一个位置的 binarySearch 方法,right 的初始值为 nums.size(),而不是 nums.size() - 1。先看以下示例:
nums = [2,2], target = 2
如果 right 的取值为 nums.size() - 1,那么在查找最后一个位置时,binarySearch(nums, target + 1) - 1 = 1 - 1 = 0。
- 这是因为
binarySearch只会返回[0, nums.size() - 1]范围的值,对于binarySearch([2,2], 3),我们希望返回3插入nums中的位置,也就是数组最后一个位置再往后一个位置,即nums.size()。 - 所以我们需要将
right的取值为nums.size(),从而使得binarySearch返回的区间更大,能够覆盖right大于nums最后一个元素的情况。
🍁代码:(C++、Java)
C++
class Solution {
private:
int binarySearch(vector<int>& nums, int target){//查找第一个位置
int left = 0, right = nums.size();
while(left < right){
int mid = left + (right - left) / 2;
if(nums[mid] >= target){
right = mid;
}else{
left = mid + 1;
}
}
return left;
}
public:
int search(vector<int>& nums, int target) {
int first = binarySearch(nums, target);
int last = binarySearch(nums, target + 1);
return (first == nums.size() || nums[first] != target) ? 0 : last - first;
}
};
Java
class Solution {
private int binarySearch(int[] nums, int target){//查找第一个位置
int left = 0, right = nums.length;
while(left < right){
int mid = left + (right - left) / 2;
if(nums[mid] >= target){
right = mid;
}else{
left = mid + 1;
}
}
return left;
}
public int search(int[] nums, int target) {
int first = binarySearch(nums, target);
int last = binarySearch(nums, target + 1);
return (first == nums.length || nums[first] != target) ? 0 : last - first;
}
}
🚀 运行结果:
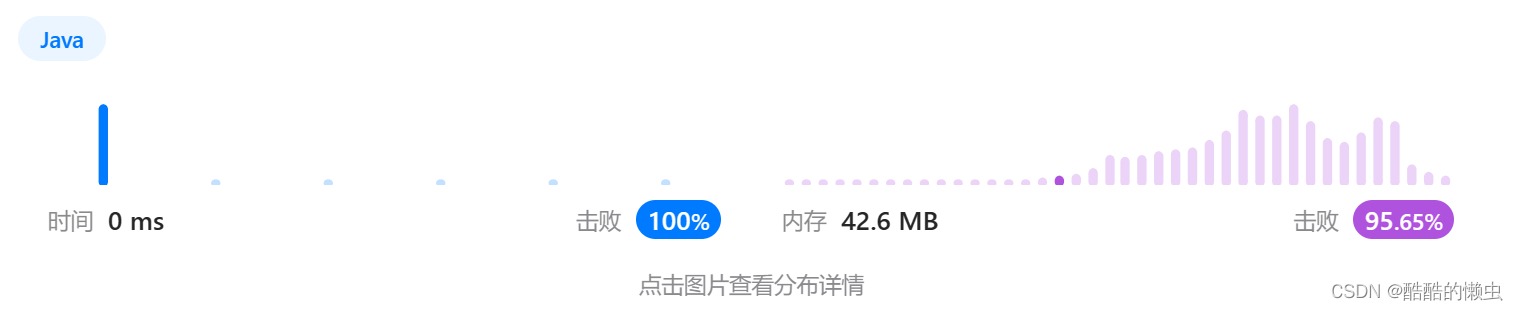
🕔 复杂度分析:
- 时间复杂度: O ( l o g n ) O(logn) O(logn),其中 nnn 为数组的长度。二分查找的时间复杂度为 O ( l o g n ) O(logn) O(logn),一共会执行两次,因此总时间复杂度为 O ( l o g n ) O(logn) O(logn)。
- 空间复杂度: O ( 1 ) O(1) O(1),只需要常数空间存放若干变量。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!