摘要

在大规模不完全知识图谱上回答复杂的逻辑查询是一项基础性但具有挑战性的任务。最近，一种解决这个问题的很有前途的方法是将KG实体和查询嵌入到向量空间中，这样回答查询的实体紧密嵌入在查询附近。然而，先前的工作 将查询建模为向量空间中的单点 ，这是有问题的，因为复杂的查询表示其答案实体的潜在大集合，但尚不清楚如何将这样的集合表示为单点。此外先前工作只能处理使用连词（∧）和存在量词（ ∃ ）的查询。处理具有逻辑或（∨）的查询仍然是一个悬而未决的问题。

将查询建模为向量空间中的单点意味着将查询表示为向量空间中的一个点。在信息检索和自然语言处理中，常常使用向量空间模型（Vector Space Model）来表示文本和查询。向量空间模型将文本表示为多维向量，其中每个维度代表一个特征或属性。这些特征可以是词语、短语、关键词的存在与否，或者其他统计信息。通过将文本映射到向量空间，可以方便地进行计算和相似性比较。

在这里，我们提出了QUERY2Box，这是一个基于嵌入的框架，用于在大量和不完整的KGs中用∧、∨和 ∃运算符推理的任意查询。

主要观点是，查询可以嵌入为box——超矩形（Hyper-rectangle） ，其中矩阵内的一组点对应于查询的一组答案实体。我们证明了连接可以自然地表示为box的交集，并证明了一个否定的结果——处理“或∨”需要 与KG实体的数量成比例的维数 。然而，通过将查询转换为 合取范式（Disjunctive Normal Form（DNF）） ，QUERY2BOx能够以可扩展的方式处理具有∧、∨和 ∃的任意逻辑查询。

Hyper-rectangle（超矩形）是一个在多维空间中表示的几何形状。也被称为"axis-aligned rectangle"（轴对齐矩形）或"axis-aligned bounding box"（轴对齐边界框）。
在二维空间中，矩形由四条边组成，且所有边都与坐标轴平行。类似地，在多维空间中，超矩形由多个轴对齐的边界构成，边界与每个维度的坐标轴平行。`
例如，在二维空间中，一个超矩形可以由左下角和右上角两个点定义。这两个点的坐标分别表示矩形的最小和最大边界值。在三维空间中，超矩形则由一个底部前角和一个顶部后角来定义。

与KG实体的数量成比例的维数
在知识图谱中，实体代表现实世界中的具体事物、概念或实体对象，而维度则表示对实体进行描述和分类的属性或特征。例如，在一个电影知识图谱中，实体可以是具体的电影作品，而维度可以包括电影的标题、导演、演员、上映日期等属性。"数量成比例的维数"意味着知识图谱中的实体数量与维度数量之间存在一种比例关系。换句话说，随着实体数量的增加，维度数量也相应地增加，而且它们之间的增长趋势是相似的。

合取范式 Disjunctive Normal Form（DNF）
是一种逻辑表达式的标准化形式，其中逻辑表达式由多个逻辑项（terms）通过逻辑或（disjunction）连接而成。
DNF 是一种将逻辑表达式表示为逻辑项的集合的方法，其中每个逻辑项都是由多个逻辑变量或它们的否定组成，并通过逻辑与（conjunction）连接。每个逻辑项代表了一个满足整个逻辑表达式的特定条件。
在 DNF 中，逻辑或连接符表示为"∨"（或者用"+“表示），逻辑与连接符表示为"∧”（或者用"·"表示）。举个例子，考虑逻辑表达式 (A ∧ B) ∨ (¬C ∧ D)，它包含了两个逻辑项：(A ∧ B) 和 (¬C ∧ D)。这个表达式在 DNF 中的表示就是这两个逻辑项的逻辑或连接：(A ∧ B) ∨ (¬C ∧ D)。
DNF 的一个重要特点是，它能够完全表示逻辑表达式的真值表。也就是说，通过将逻辑表达式转换为 DNF，可以清晰地表示逻辑表达式的所有可能真值情况。

最后演示了QUERY2BOx在三个大型KG上的有效性，并表明QUERY 2BOx比现有技术实现了高达25%的相对改进。

介绍

知识图谱捕获实体之间不同类型的关系。在KG上回答任意的逻辑问题在基于知识推理、已经更广泛的人工智能的一项基本任务。

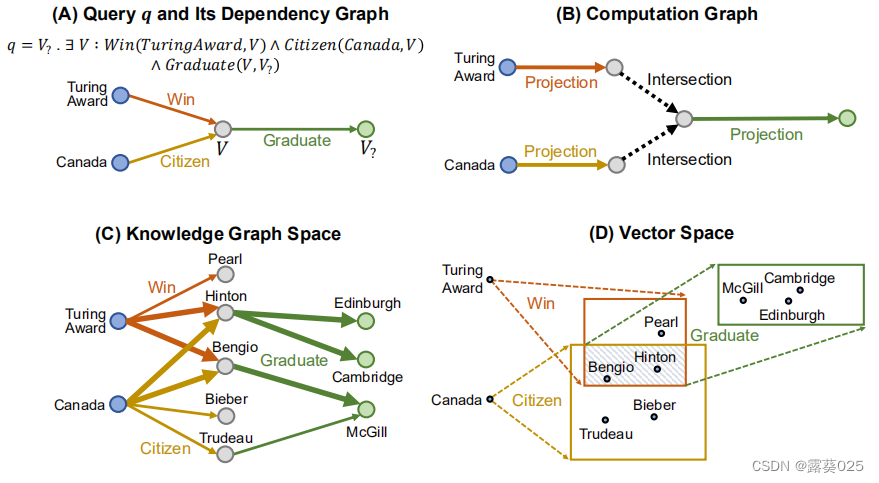
一阶逻辑查询可以表示为有向非循环图（DAG）（图1 A），并根据DAG进行推理以获得一组答案（图1 C）。这种方法虽然简单直观，但也有很多缺点：
（1）子图匹配的计算复杂度是查询大小的指数，因此无法扩展到现代KGs；
（2） 子图匹配非常敏感，因为它不能正确回答缺少关系的查询。

为了补救（2），可以 填补缺失关系，但这只会使KG密度更大，这将进一步加剧问题（1）。

“Impute missing relations”（填补缺失关系）
指在数据分析和机器学习任务中，通过使用已有数据的模式和特征来推断或估计缺失的关系信息。
在现实世界的数据集中，可能存在一些缺失的关系数据。这些缺失的关系可能是由于数据收集过程中的错误、不完整的记录或其他原因导致的。然而，缺失的关系数据对于分析和建模任务可能是重要的，因为它们可能包含有关数据之间关系的有价值信息。
因此，"impute missing relations"的目标是通过利用已有的数据和模型来填补这些缺失的关系。填补缺失的关系数据可以提高数据的完整性和可用性，使得后续的分析和建模任务更加准确和全面。

最近，出现了一种很有前景的替代方法——将逻辑查询和KG实体嵌入到低维向量空间中，从而 将回答查询的实体嵌入到查询附近。这种方法稳健地处理缺失的关系，并且也是快一个数量级 ，因为回答任意逻辑查询被简化为简单地识别向量空间中最接近查询嵌入的实体。

将逻辑查询和知识图谱（KG）实体嵌入到低维向量空间中的目标是将查询和相关实体表示为向量，并通过计算它们之间的相似度来回答查询并找到与查询相关的实体。
一旦逻辑查询和KG实体都被映射为向量表示，就可以使用向量之间的相似度度量（如余弦相似度）来计算查询向量与实体向量之间的相似性。通过找到与查询向量最相似的实体向量，可以将回答查询的实体嵌入到查询附近。

然而，先前的工作将查询嵌入到向量空间中的单个点中，这是有问题的，因为回答逻辑查询需要在遍历KG时对一组活动实体进行建模（图1 C），且如何有效地对具有单点的集合进行建模尚不清楚。此外，在向量空间中定义两点的逻辑运算符（例如，集合交集）也是不自然的。先前工作的另一个基本限制是，它只能处理 合取查询（conjunctive queries） ，这是一个一阶逻辑的子集，只涉及连词（∧）和存在量词（∃），而不是逻辑或（∨）。如何在向量空间中有效地处理或关系（∨）仍然是一个悬而未决的问题。

Conjunctive queries（合取查询,∧）
在合取查询中，查询条件由多个子条件（谓词条件）通过逻辑与（合取）连接而成。每个子条件由一个谓词和对应的参数组成，用于描述所需的数据或关系。在知识图谱中，合取查询也常用于从图结构中获取满足特定关系和属性条件的实体和关系。它可以用于查询图谱中的实体间的关系、实体属性的限制等。

本文提出了QUERY2Box，这是一个基于嵌入的KG推理框架，能够以可扩展的方式处理任意 存在性正向一阶逻辑（EPFO） 逻辑查询（即包括∧、∨和∃的集合的查询）。

Existential Positive First-order（EPFO，存在性正向一阶逻辑）是一种子集逻辑，属于一阶逻辑的变种。在EPFO中，只允许存在量词（存在量词）和正向的原子命题（正向谓词）。
EPFO限制了逻辑表达式的形式，以便更简化和限定推理过程。它不允许否定（否定量词和否定谓词）的使用，只允许存在量词和正向谓词的组合。
在EPFO中，常见的逻辑表达式形式如下：
1.原子命题：P(x, y, z)，表示一个具有参数 x、y、z 的正向谓词。
2.存在量化：∃x P(x)，表示存在一个 x，使得谓词 P 成立。
EPFO的一个重要特点是它的计算复杂性较低。由于限制了逻辑表达式的形式，EPFO的推理过程相对较简单和高效，使得它适用于某些特定的推理任务。

首先，为了准确地对一组实体进行建模，我们的关键思想是使用 闭合区域（closed region），而不是向量空间中的单个点。
具体来说，我们使用一个方box（轴对齐的超矩形）来表示查询（图1 D）。这提供了三个重要的好处：
（1）box自然地对它们所包含的实体集进行建模；
（2）逻辑运算符（例如，集合交集）可以自然地在方框上定义，类似于Venn图；
（3）在框上执行逻辑计算器会产生新的框，这意味着操作已关闭；

因此，通过根据查询计算图迭代更新框，可以在QUERY2框中有效地执行逻辑搜索（图1 B、D）。

“closed region”（闭合区域）
知识图谱中是指一个由实体和关系构成的子图，其中所有的路径都是闭合的，即从一个实体出发，沿着关系边遍历若干步后最终回到同一实体。这个闭合路径可以是简单的环（环状路径），也可以是更复杂的图形结构（包含多个环的区域）。闭合区域在知识图谱中的应用主要是用于表示实体之间的密切关联和相互作用。当一个区域内的实体之间存在多个路径时，这些实体往往具有较高的相关性或相似性。
通过识别和分析闭合区域，可以揭示实体之间的隐藏关系、发现新的关联模式，并支持知识图谱的查询和推理。

我们展示了QUERY2Box可以自然地处理关系与(∧)的查询。首先证明了一个否定的结果——仅将EPFO查询嵌入到单个点或框是难以处理的，因为它需要嵌入与KG实体数量成比例的维数。然而，我们提供了一个的解决方案——将给定的EPFO逻辑查询转换为合取范式（DNF），即 合取查询的析取 。

“disjunction of conjunctive queries”（合取查询的析取）
指的是通过逻辑或（disjunction）将多个合取查询（conjunctive queries）进行组合的查询形式。
合取查询是一种查询形式，其中多个条件通过逻辑与（合取）进行连接。每个条件通常由谓词和参数组成，以描述实体和它们的属性或关系。而析取查询则是将多个查询通过逻辑或进行连接，以获取满足任一查询的结果。在知识图谱中，可以将多个合取查询形式的条件通过逻辑或操作符进行组合，以构建一个析取查询。这个析取查询将多个查询条件同时考虑，返回满足任一查询条件的结果集。
例如，假设有以下合取查询条件：
查询1：Person(x), Age(x) > 30
查询2：Employee(y), Salary(y) > 50000
这两个合取查询分别表示找到年龄大于30的人和薪水高于50000的雇员。通过将这两个查询进行析取操作，可以得到一个析取查询，形式如下：
查询3：(Person(x), Age(x) > 30) OR (Employee(y), Salary(y) > 50000)
查询3表示找到满足年龄大于30的人或薪水高于50000的雇员。执行这个析取查询将返回同时满足任一条件的结果。