数组
数组可以说是最简单的一种数据结构,它占据一块连续的内存并按照顺序存储数据。创建数组时,我们需要首先指定数组的容量大小,然后根据大小分配内存。即使我们只在数组中存储一个数字,也需要为所有的数据预先分配内存。因此数组的空间效率不是很好,经常会有空闲的区域没有得到充分利用。
由于数组中的内存是连续的,于是可以根据下标在O(1)时间读/写任何元素,因此它的时间效率是很高的。我们可以根据数组时间效率高的优点,用数组来实现简单的哈希表:把数组的下标设为哈希表的键值(Key),而把数组中的每一个数字设为哈希表的值(Value),这样每一个下标及数组中该下标对应的数字就组成了一个键值-值的配对。有了这样的哈希表,我们就可以在O(1)实现查找,从而可以快速高效地解决很多问题。
为了解决数组空间效率不高的问题,人们又设计实现了多种动态数组,比如C++的STL中的vector。为了避免浪费,我们先为数组开辟较小的空间,然后往数组中添加数据。当数据的数目超过数组的容量时,我们再重新分配一块更大的空间(STL的 vector每次扩充容量时,新的容量都是前一次的两倍),把之前的数据复制到新的数组中,再把之前的内存释放,这样就能减少内存的浪费。但我们也注意到每一次扩充数组容量时都有大量的额外操作,这对时间性能有负面影响,因此使用动态数组时要尽量减少改变数组容量大小的次数。
在C/C++中,数组和指针是相互关联又有区别的两个概念。当我们声明一个数组时,其数组的名字也是一个指针,该指针指向数组的第一个元素。我们可以用一个指针来访问数组。但值得注意的是,C/C++没有记录数组的大小,因此用指针访问数组中的元素时,程序员要确保没有超出数组的边界。下面通过一个例子来了解数组和指针的区别。运行下面的代码,请问输出是什么?
int GetSize(int data[])
{
return sizeof(data);
}
int main(int argc, char* argv[])
{
int data[] = {1,2,3,4,5};
int size1 = sizeof(data1);
int* data2 = data1;
int size2 = sizeof(data2);
int size3 = GetSize(data1);
printf("%d, %d, %d", size1, size2, size3);
}
答案是输出“20,4,4”。data1是一个数组,sizeof(data1)是求数组的大小。这个数组包含5个整数,每个整数占4字节,因此总共是20字节。data2声明为指针,尽管它指向了数组data1的第一个数字,但它的本质仍然是一个指针。在32位系统上,对任意指针求sizeof,得到的结果都是4。在C/C++中,当数组作为函数的参数进行传递时,数组就自动退化为同类型的指针。因此尽管函数GetSize的参数data被声明为数组,但它会退化为指针,size3的结果仍然是4。
二维数组中的查找
题目:在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的个二维数组和一个整数,判断数组中是否含有该整数。
例如下面的二维数组就是每行、每列都递增排序。如果在这个数组中查找数字7,则返回true;如果查找数字5,由于数组不含有该数字,则返回false。
1 2 8 9
2 4 9 12
4 7 10 13
6 8 11 15
在分析这个问题的时候,很多应聘者都会把二维数组画成矩形,然后从数组中选取一个数字,分3种情况来分析查找的过程。当数组中选取的数字刚好和要查找的数字相等时,就结束查找过程。如果选取的数字小于要查找的数字,那么根据数组排序的规则,要查找的数字应该在当前选取的位置的右边或者下边(如图2.1 (a)所示)。同样,如果选取的数字大于要查找的数字,那么要查找的数字应该在当前选取的位置的上边或者左边(如图2.1(b)所示)。
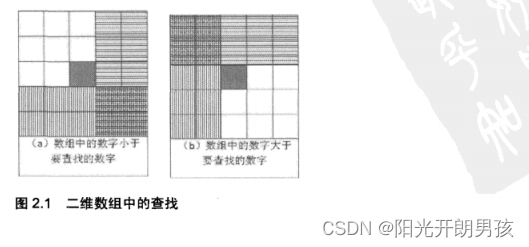
注:在数组中间选择一个数(深色方格),根据它的大小判断要查找的数字可能出现的区域(阴影部分)。
在上面的分析中,由于要查找的数字相对于当前选取的位置有可能在两个区域中出现,而且这两个区域还有重叠,这问题看起来就复杂了,于是很多人就卡在这里束手无策了。
当我们需要解决一个复杂的问题时,一个很有效的办法就是从一个具体的问题入手,通过分析简单具体的例子,试图寻找普遍的规律。针对这个问题,我们不妨也从一个具体的例子入手。下面我们以在题目中给出的数组中查找数字7为例来一步步分析查找的过程。
前面我们之所以遇到难题,是因为我们在二维数组的中间选取一个数字来和要查找的数字做比较,这样导致下一次要查找的是两个相互重叠的区域。如果我们从数组的一个角上选取数字来和要查找的数字做比较,情况会不会变简单呢?
首先我们选取数组右上角的数字9。由于9大于7,并且9还是第4列的第一个(也是最小的)数字,因此7不可能出现在数字9所在的列。于是我们把这一列从需要考虑的区域内剔除,之后只需要分析剩下的3列(如图2.2(a)所示)。在剩下的矩阵中,位于右上角的数字是8。同样8大于7,因此8所在的列我们也可以剔除。接下来我们只要分析剩下的两列即可(如图2.2(b)所示)。
在由剩余的两列组成的数组中,数字2位于数组的右上角。2小于7,那么要查找的7可能在2的右边,也有可能在2的下边。在前面的步骤中,我们已经发现⒉右边的列都已经被剔除了,也就是说7不可能出现在2的右边,因此7只有可能出现在2的下边。于是我们把数字2所在的行也剔除,只分析剩下的三行两列数字(如图2.2©所示)。在剩下的数字中,数字4位于右上角,和前面一样,我们把数字4所在的行也删除,最后剩下两行两列数字(如图2.2 (d)所示)。
在剩下的两行两列4个数字中,位于右上角的刚好就是我们要查找的数字7,于是查找过程就可以结束了。

注:矩阵中加阴影背景的区域是下一步查找的范围
总结上述查找的过程,我们发现如下规律:首先选取数组中右上角的数字。如果该数字等于要查找的数字,查找过程结束;如果该数字大于要查找的数字,剔除这个数字所在的列;如果该数字小于要查找的数字,剔除这个数字所在的行。也就是说如果要查找的数字不在数组的右上角,则每一次都在数组的查找范围中剔除一行或者一列,这样每一步都可以缩小查找的范围,直到找到要查找的数字,或者查找范围为空。
把整个查找过程分析清楚之后,我们再写代码就不是一件很难的事情了。下面是上述思路对应的参考代码:
代码示例
#include <cstdio>
bool Find(int* matrix, int rows, int columns, int number)
{
bool found = false;
if (matrix != nullptr && rows > 0 && columns > 0)
{
int row = 0;
int column = columns - 1;
while (row < rows && column >= 0)
{
if (matrix[row * columns + column] == number)
{
found = true;
break;
}
else if (matrix[row * columns + column] > number)
--column;
else
++row;
}
}
return found;
}
// ====================测试代码====================
void Test(const char* testName, int* matrix, int rows, int columns, int number, bool expected)
{
if (testName != nullptr)
printf("%s begins: ", testName);
bool result = Find(matrix, rows, columns, number);
if (result == expected)
printf("Passed.\n");
else
printf("Failed.\n");
}
// 1 2 8 9
// 2 4 9 12
// 4 7 10 13
// 6 8 11 15
// 要查找的数在数组中
void Test1()
{
int matrix[][4] = { {1, 2, 8, 9}, {2, 4, 9, 12}, {4, 7, 10, 13}, {6, 8, 11, 15} };
Test("Test1", (int*)matrix, 4, 4, 7, true);
}
// 1 2 8 9
// 2 4 9 12
// 4 7 10 13
// 6 8 11 15
// 要查找的数不在数组中
void Test2()
{
int matrix[][4] = { {1, 2, 8, 9}, {2, 4, 9, 12}, {4, 7, 10, 13}, {6, 8, 11, 15} };
Test("Test2", (int*)matrix, 4, 4, 5, false);
}
// 1 2 8 9
// 2 4 9 12
// 4 7 10 13
// 6 8 11 15
// 要查找的数是数组中最小的数字
void Test3()
{
int matrix[][4] = { {1, 2, 8, 9}, {2, 4, 9, 12}, {4, 7, 10, 13}, {6, 8, 11, 15} };
Test("Test3", (int*)matrix, 4, 4, 1, true);
}
// 1 2 8 9
// 2 4 9 12
// 4 7 10 13
// 6 8 11 15
// 要查找的数是数组中最大的数字
void Test4()
{
int matrix[][4] = { {1, 2, 8, 9}, {2, 4, 9, 12}, {4, 7, 10, 13}, {6, 8, 11, 15} };
Test("Test4", (int*)matrix, 4, 4, 15, true);
}
// 1 2 8 9
// 2 4 9 12
// 4 7 10 13
// 6 8 11 15
// 要查找的数比数组中最小的数字还小
void Test5()
{
int matrix[][4] = { {1, 2, 8, 9}, {2, 4, 9, 12}, {4, 7, 10, 13}, {6, 8, 11, 15} };
Test("Test5", (int*)matrix, 4, 4, 0, false);
}
// 1 2 8 9
// 2 4 9 12
// 4 7 10 13
// 6 8 11 15
// 要查找的数比数组中最大的数字还大
void Test6()
{
int matrix[][4] = { {1, 2, 8, 9}, {2, 4, 9, 12}, {4, 7, 10, 13}, {6, 8, 11, 15} };
Test("Test6", (int*)matrix, 4, 4, 16, false);
}
// 鲁棒性测试,输入空指针
void Test7()
{
Test("Test7", nullptr, 0, 0, 16, false);
}
int main(int argc, char* argv[])
{
Test1();
Test2();
Test3();
Test4();
Test5();
Test6();
Test7();
return 0;
}
在前面的分析中,我们每一次都是选取数组查找范围内的右上角数字。同样,我们也可以选取左下角的数字。感兴趣的读者不妨自己分析一下每次都选取左下角的查找过程。但我们不能选择左上角或者右下角。以左上角为例,最初数字1位于初始数组的左上角,由于1小于7,那么7应该位于1的右边或者下边。此时我们既不能从查找范围内剔除1所在的行,也不能剔除1所在的列,这样我们就无法缩小查找的范围。
测试用例
1)二维数组中包含查找的数字(查找的数字是数组中的最大值和最小值,查找的数字介于数组中的最大值和最小值之间)。
2)二维数组中没有查找的数字(查找的数字大于数组中的最大值,查找的数字小于数组中的最小值,查找的数字在数组的最大值和最小值之间但数组中没有这个数字)。
3)特殊输入测试(输入空指针)。
考点
二维数组在内存中占据连续的空间。在内存中从上到下存储各行元素,在同一行中按照从左到右的顺序存储。因此我们可以根据行号和列号计算出相对于数组首地址的偏移量,从而找到对应的元素。
当应聘者发现问题比较复杂时,能不能通过具体的例子找出其中的规律,是能否解决这个问题的关键所在。这个题目只要从一个具体的二维数组的右上角开始分析,就能找到查找的规律,从而找到解决问题的突破口。