注意力机制-基础

基础部分比较简单，全是搬运，主要介绍几个例子。
主要是搬运来的：动手学深度学习

心理学

人类的注意力是有限的、有价值和稀缺的资源。而环境中的干扰注意力的信息却并不少。 比如人类的视觉神经系统大约每秒收到
位的信息， 这远远超过了大脑能够完全处理的水平。 幸运的是，人类的祖先已经从经验（也称为数据）中认识到 “并非感官的所有输入都是一样的”。 在整个人类历史中，这种只将注意力引向感兴趣的一小部分信息的能力， 使人类的大脑能够更明智地分配资源来生存、成长和社交， 例如发现天敌、找寻食物和伴侣。

注意力在视觉世界中的应用有两种：1. 非自主性提示， 2. 自主性提示

非自主性提示

非自主性提示是基于环境中物体的突出性和易见性。假如眼前有一份黑白色报纸、一篇黑白色研究论文、一个红色咖啡杯、一本黑白色笔记本和一本黑白色书。所有纸制品都是黑白印刷的，但咖啡杯是红色的。 换句话说，这个咖啡杯在这种视觉环境中是突出和显眼的， 不由自主地引起人们的注意。 所以我们会把视力最敏锐的地方放到咖啡上。

自主性提示

假如我们想要看书，与非自主性提示的由于突出性导致的选择不同，我们选择书是受到了认知和意识的控制， 因此注意力在基于自主性提示去辅助选择时将更为谨慎。 受试者的主观意愿推动，选择的力量也就更强大。

查询、键和值

自主性的与非自主性的注意力提示解释了人类的注意力的方式， 下面来看看如何通过这两种注意力提示， 用神经网络来设计注意力机制的框架，

首先，考虑一个相对简单的状况， 即只使用非自主性提示。 要想将选择偏向于感官输入， 则可以简单地使用参数化的全连接层， 甚至是非参数化的最大汇聚层或平均汇聚层。

因此，“是否包含自主性提示”将注意力机制与全连接层或汇聚层区别开来。

在注意力机制的背景下，自主性提示被称为查询（query）。给定任何查询，注意力机制通过注意力汇聚（attention pooling） 将选择引导至感官输入（sensory inputs，例如中间特征表示）。 在注意力机制中，这些感官输入被称为值（value）。 更通俗的解释，每个值都与一个键（key）配对， 这可以想象为感官输入的非自主提示。 如下图所示，可以通过设计注意力汇聚的方式， 便于给定的查询（自主性提示）与键（非自主性提示）进行匹配， 这将引导得出最匹配的值（感官输入）。

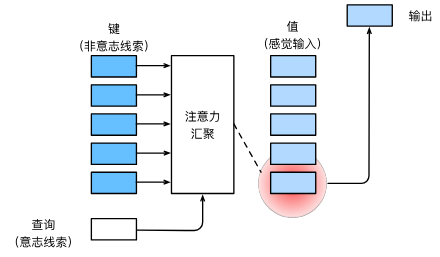
图（10.1.3）

注意力汇聚：Nadaraya-Watson 核回归

上节介绍了注意力机制的主要成分： 查询（自主提示）和键（非自主提示）之间的交互形成了注意力汇聚； 注意力汇聚有选择地聚合了值（感官输入）以生成最终的输出。 1964年提出的Nadaraya-Watson核回归模型 是一个简单但完整的例子，可以用于演示具有注意力机制的机器学习。

简单起见, 考虑下面这个回归问题：给定的成对的“输入一输出”数据集 { ( x 1 , y 1 ) , … , ( x n , y n ) } \left\{\left(x_1, y_1\right), \ldots,\left(x_n, y_n\right)\right\} {(x1​,y1​),…,(xn​,yn​)}如何学习$f$来预测任意新输入$x$的输出$\hat{y}=f(x)$?
上面这个数据集即为训练集，并且是由
$y_i=2\sin \left(x_i\right)+x_i^{0.8}+ϵ(\mathrm{10.2.1})$
生成，$ϵ$服从均值为0，标准差为0.5的正态分布，是噪声项。示例中生成了50个样本。

平均汇聚

最简单的，基于平均汇聚来做，
$f(x)=\frac{1}{n}{\sum }_{i=1}^n{y}_i(\mathrm{10.2.2})$

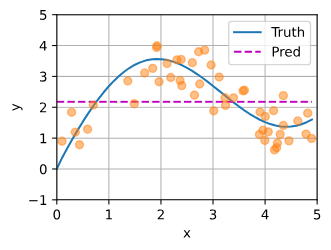
上图为结果，预测就是一个常值。效果很差。

非参数注意力汇聚

显然，平均汇聚忽略了输入
。 于是Nadaraya和 Watson提出了一个更好的想法， 根据输入的位置对输出
进行加权：
$f(x)={\sum }_{i=1}^n\frac{K\left(x-x_i\right)}{{\sum }_{j=1}^{n}K\left(x-x_j\right)}{y}_i（\mathrm{10.2.3}）$
很像softmax，其中$K$是核（kernel）。 上式所描述的估计器被称为 Nadaraya-Watson核回归（Nadaraya-Watson kernel regression）。 这里不会深入讨论核函数的细节， 但受此启发， 我们可以从 图10.1.3中的注意力机制框架的角度 重写 (10.2.3)， 成为一个更加通用的注意力汇聚（attention pooling）公式：
$f(x)={\sum }_{i=1}^n\alpha \left(x,x_i\right)y_i(\mathrm{10.2.4})$

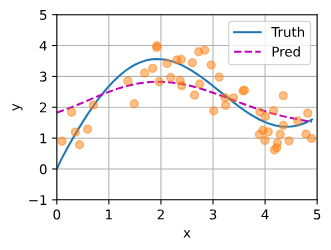
值得注意的是，Nadaraya-Watson核回归是一个非参数模型。 因此， (10.2.6)是 非参数的注意力汇聚（nonparametric attention pooling）模型。 接下来，我们将基于这个非参数的注意力汇聚模型来绘制预测结果。 从绘制的结果会发现新的模型预测线是平滑的，并且比平均汇聚的预测更接近真实。

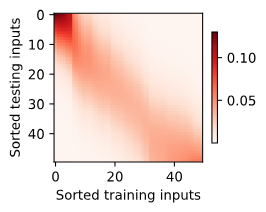
现在来观察注意力的权重。 这里测试数据的输入相当于查询，而训练数据的输入相当于键。 因为两个输入都是经过排序的，因此由观察可知“查询-键”对越接近， 注意力汇聚的注意力权重就越高。

带参数注意力汇聚

非参数的Nadaraya-Watson核回归具有一致性（consistency）的优点： 如果有足够的数据，此模型会收敛到最优结果。 尽管如此，我们还是可以轻松地将可学习的参数集成到注意力汇聚中。

实现这个模型就很简单了，可以简单滴用MSE损失和SGD进行优化。看下训练结果：

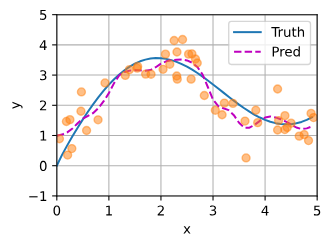
很明显，拟合得更好了，但曲线不平滑了，D2L中说：与非参数的注意力汇聚模型相比， 带参数的模型加入可学习的参数后， 曲线在注意力权重较大的区域变得更不平滑。

d2l的讨论区也有很多人在讨论这个问题，可以去看看。