C++ 二叉树(建立、销毁、前中后序遍历和层次遍历，寻找双亲结点等)

（1）结构体和类定义

struct BTreeNode {
	T data;
	BTreeNode* left, * right;
	BTreeNode() :data(0), left(nullptr), right(nullptr) {}
	BTreeNode(T val, BTreeNode<T>* leftChild = nullptr, BTreeNode<T>* rightChild = nullptr)
		:data(val), left(leftChild), right(rightChild) {}

};

template<class T>
class BTree {
public:
	BTree() :root(nullptr) {}										      // 构造函数
	BTree(string str);                                                    // 重载

	void createTree(BTreeNode<T>*& bt, string str);                       // 创建二次树
	~BTree();														      // 析构函数
	bool IsEmpty();													      // 判二叉树空否？
	int Size(BTreeNode<T>* cur);                                          // 计算结点个数
	int getSize();                                                        // 获取结点个数
	BTreeNode<T>* getData(T& item, BTreeNode<T>* cur);	                  // 取得结点数据
	bool Find(T& item);		                                              // 判断item是否在树中
	int Height(BTreeNode<T>* bt);                                         // 求树高度
	int getHeight();                                                      // 获取树高度
	BTreeNode<T>* getRoot();	                                          // 取根

	void preOrderTraversal(BTreeNode<T>* cur, vector<int>& vec);          // 前序遍历
	void inOrderTraversal(BTreeNode<T>* cur, vector<int>& vec);		      // 中序遍历
	void postOrderTraversal(BTreeNode<T>* cur, vector<int>& vec);         // 后序遍历
	void levelOrderTraversal(BTreeNode<T>* cur, vector<int>& vec);        // 层序遍历

	vector<T> preOrder();						                          // 调用前序遍历，返回vector
	vector<T> inOrder();											      // 调用中序遍历，返回vector
	vector<T> postOrder();											      // 调用后序遍历，返回vector
	vector<T> levelOrder();                                               // 调用层序遍历，返回vector

	void CopyTree(BTreeNode<T>* root, BTreeNode<T>*& copyRoot);           // 二叉树复制
	void Copy(BTreeNode<T>*& copyRoot);                                   // 调用二叉树复制
	void destroyCopyTree(BTreeNode<T>*& copyRoot);                        // 销毁复制二叉树


	BTreeNode<T>* FindParent(BTreeNode<T>* root, BTreeNode<T>* node);     // 寻找双亲
	BTreeNode<T>* LeftChild(BTreeNode<T>* node) {                         //求结点 node 的左孩子
		return (node != nullptr) ? node->left : nullptr;
	}
	BTreeNode<T>* RightChild(BTreeNode<T>* node) {                        //求结点 node 的右孩子
		return (node != nullptr) ? node->right : nullptr;
	}

protected:
	BTreeNode<T>* root;
	void destroyTree(BTreeNode<T>* node);                                // 销毁二叉树
};

（2）创建二叉树

template<class T>
BTree<T>::BTree(string str) {
	createTree(root, str);
	cout << "报告：创建一颗二叉树，完成！！！" << endl;
}

template<class T>
void BTree<T>::createTree(BTreeNode<T>*& bt, string str) {
	static int i = 0;
	char ch = ' ';
	ch = str[i++];

	if (ch == '#') bt = nullptr;
	else {
		bt = new BTreeNode<T>(ch);
		createTree(bt->left, str);
		createTree(bt->right, str);
	}
};

（3）前中后序遍历和层序遍历

// 前序遍历
template<class T>
void BTree<T>::preOrderTraversal(BTreeNode<T>* cur, vector<int>& vec) {
	if (cur == nullptr)
		return;
	vec.push_back(cur->data);           // 中
	preOrderTraversal(cur->left, vec);  // 左
	preOrderTraversal(cur->right, vec); // 右
}

// 调用前序遍历，返回vector
template<class T>
vector<T> BTree<T>::preOrder() {
	cout << "获取前序遍历数组...." << endl;
	cout << ">>>>";
	vector<T> resVec;
	preOrderTraversal(root, resVec);
	return resVec;
}

// 中序遍历
template<class T>
void BTree<T>::inOrderTraversal(BTreeNode<T>* cur, vector<int>& vec) {
	if (cur == nullptr)
		return;
	inOrderTraversal(cur->left, vec);  // 左
	vec.push_back(cur->data);          // 中
	inOrderTraversal(cur->right, vec); // 右
}

// 调用中序遍历，返回vector
template<class T>
vector<T> BTree<T>::inOrder() {
	cout << "获取中序遍历数组...." << endl;
	cout << ">>>>";
	vector<T> resVec;
	inOrderTraversal(root, resVec);
	return resVec;
}

// 后序遍历
template<class T>
void BTree<T>::postOrderTraversal(BTreeNode<T>* cur, vector<int>& vec) {
	if (cur == nullptr)
		return;
	postOrderTraversal(cur->left, vec);  // 左
	postOrderTraversal(cur->right, vec); // 右
	vec.push_back(cur->data);            // 中
}

// 调用后序遍历，返回vector
template<class T>
vector<T> BTree<T>::postOrder() {
	cout << "获取后序遍历数组...." << endl;
	cout << ">>>>";
	vector<T> resVec;
	postOrderTraversal(root, resVec);
	return resVec;
}

// 层序遍历
template<class T>
void BTree<T>::levelOrderTraversal(BTreeNode<T>* cur, vector<int>& vec) {
	if (cur == nullptr) return;
	queue<BTreeNode<T>*> Queue;
	BTreeNode<T>* p;
	Queue.push(cur); // 根结点入队列
	while (!Queue.empty()) {
		p = Queue.front();
		//cout << p->data << " ";//输出出队结点的数据
		vec.push_back(p->data);
		Queue.pop();
		if (p->left != nullptr) {
			Queue.push(p->left);
		}
		if (p->right != nullptr) {
			Queue.push(p->right);
		}
	}
}

// 调用层序遍历，返回vector
template<class T>
vector<T> BTree<T>::levelOrder() {
	cout << "获取层序遍历数组...." << endl;
	cout << ">>>>";
	vector<T> resVec;
	levelOrderTraversal(root, resVec);
	return resVec;
}

（4）复制二叉树

template<class T>
void BTree<T>::CopyTree(BTreeNode<T>* root, BTreeNode<T>*& copyRoot) {
	if (!root) {
		copyRoot = nullptr;
	}
	else {
		copyRoot = new BTreeNode<T>;
		copyRoot->data = root->data;           //复制根节点
		CopyTree(root->left, copyRoot->left);  //递归复制左子树
		CopyTree(root->right, copyRoot->right);//递归复制左子树
	}
}

template<class T>
void BTree<T>::Copy(BTreeNode<T>*& copyRoot) {
	CopyTree(root, copyRoot);
}

（5）销毁二叉树

template<class T>
void BTree<T>::destroyCopyTree(BTreeNode<T>*& copyRoot) {
	destroyTree(copyRoot);
	cout << "报告，复制二叉树已销毁完毕!!!" << endl;
}

// 销毁二叉树 
template<class T>
void BTree<T>::destroyTree(BTreeNode<T>* bt) {
	// 后序遍历删除根为subTree的子树；
	if (bt != nullptr) {
		destroyTree(bt->left);    //删除左子树
		destroyTree(bt->right);   //删除右子树
		delete bt; 			      //删除根结点
	}
}

（6）析构函数

// 析构函数
template<class T>
BTree<T>::~BTree<T>() {
	//cout << "调用析构函数" << endl;
	destroyTree(root);
	cout << "报告，这棵树已经销毁完毕!!!" << endl;
}

（7）求树的高度

// 求树高度
template<class T>
int BTree<T>::Height(BTreeNode<T>* bt) {
	if (bt == nullptr) return 0;
	else {
		int leftH = Height(bt->left);
		int rightH = Height(bt->right);
		return (leftH > rightH) ? leftH + 1 : rightH + 1;
	}
}

// 获取树高度
template<class T>
int BTree<T>::getHeight() {
	return Height(root);
}

（8）获取结点，判断其是否在二叉树中

// 取得结点数据
template<class T>
BTreeNode<T>* BTree<T>::getData(T& item, BTreeNode<T>* cur) {
	if (cur == nullptr) return nullptr;
	if (cur->data == item) return cur;
	return getData(item, cur->left) != nullptr ? getData(item, cur->left) : getData(item, cur->right);
}

// 判断item是否在树中
template<class T>
bool BTree<T>::Find(T& item) {
	if (this->getData(item, root) == nullptr) return false;
	else return true;

（9）计算结点个数和获取结点个数

// 计算结点个数
template<class T>
int BTree<T>::Size(BTreeNode<T>* cur) {
	if (cur == nullptr)
		return 0;
	else
		return 1 + Size(cur->left) + Size(cur->right);
}

// 获取结点个数
template<class T>
int BTree<T>::getSize() {
	return Size(root);
}

（10）二叉树判空

// 判二叉树空否？
template<class T>
bool BTree<T>::IsEmpty() {
	return (root == nullptr) ? true : false;
}

（11）获取根结点

// 获取根 
template<class T>
BTreeNode<T>* BTree<T>::getRoot() {
	if (!root) return nullptr;
	else {
		return this->root;
	}
}

源代码：

btree.h

#pragma once
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

template<class T>
struct BTreeNode {
	T data;
	BTreeNode* left, * right;
	BTreeNode() :data(0), left(nullptr), right(nullptr) {}
	BTreeNode(T val, BTreeNode<T>* leftChild = nullptr, BTreeNode<T>* rightChild = nullptr)
		:data(val), left(leftChild), right(rightChild) {}

};

template<class T>
class BTree {
public:
	BTree() :root(nullptr) {}										      // 构造函数
	BTree(string str);                                                    // 重载

	void createTree(BTreeNode<T>*& bt, string str);                       // 创建二次树
	~BTree();														      // 析构函数
	bool IsEmpty();													      // 判二叉树空否？
	int Size(BTreeNode<T>* cur);                                          // 计算结点个数
	int getSize();                                                        // 获取结点个数
	BTreeNode<T>* getData(T& item, BTreeNode<T>* cur);	                  // 取得结点数据
	bool Find(T& item);		                                              // 判断item是否在树中
	int Height(BTreeNode<T>* bt);                                         // 求树高度
	int getHeight();                                                      // 获取树高度
	BTreeNode<T>* getRoot();	                                          // 取根

	void preOrderTraversal(BTreeNode<T>* cur, vector<int>& vec);          // 前序遍历
	void inOrderTraversal(BTreeNode<T>* cur, vector<int>& vec);		      // 中序遍历
	void postOrderTraversal(BTreeNode<T>* cur, vector<int>& vec);         // 后序遍历
	void levelOrderTraversal(BTreeNode<T>* cur, vector<int>& vec);        // 层序遍历

	vector<T> preOrder();						                          // 调用前序遍历，返回vector
	vector<T> inOrder();											      // 调用中序遍历，返回vector
	vector<T> postOrder();											      // 调用后序遍历，返回vector
	vector<T> levelOrder();                                               // 调用层序遍历，返回vector

	void CopyTree(BTreeNode<T>* root, BTreeNode<T>*& copyRoot);           // 二叉树复制
	void Copy(BTreeNode<T>*& copyRoot);                                   // 调用二叉树复制
	void destroyCopyTree(BTreeNode<T>*& copyRoot);                        // 销毁复制二叉树


	BTreeNode<T>* FindParent(BTreeNode<T>* root, BTreeNode<T>* node);     // 寻找双亲
	BTreeNode<T>* LeftChild(BTreeNode<T>* node) {                         //求结点 node 的左孩子
		return (node != nullptr) ? node->left : nullptr;
	}
	BTreeNode<T>* RightChild(BTreeNode<T>* node) {                        //求结点 node 的右孩子
		return (node != nullptr) ? node->right : nullptr;
	}

protected:
	BTreeNode<T>* root;
	void destroyTree(BTreeNode<T>* node);                                // 销毁二叉树
};

btree.cpp

// 每次写递归，都按照这三要素来写，可以保证大家写出正确的递归算法！
// 1.确定递归函数的参数的返回值
// 2.确定终止条件
// 3.确定单层递归的逻辑

#include "btree.h"

template<class T>
BTree<T>::BTree(string str) {
	createTree(root, str);
	cout << "报告：创建一颗二叉树，完成！！！" << endl;
}

template<class T>
void BTree<T>::createTree(BTreeNode<T>*& bt, string str) {
	static int i = 0;
	char ch = ' ';
	ch = str[i++];

	if (ch == '#') bt = nullptr;
	else {
		bt = new BTreeNode<T>(ch);
		createTree(bt->left, str);
		createTree(bt->right, str);
	}
};

// 判二叉树空否？
template<class T>
bool BTree<T>::IsEmpty() {
	return (root == nullptr) ? true : false;
}

// 计算结点个数
template<class T>
int BTree<T>::Size(BTreeNode<T>* cur) {
	if (cur == nullptr)
		return 0;
	else
		return 1 + Size(cur->left) + Size(cur->right);
}

// 获取结点个数
template<class T>
int BTree<T>::getSize() {
	return Size(root);
}

// 取得结点数据
template<class T>
BTreeNode<T>* BTree<T>::getData(T& item, BTreeNode<T>* cur) {
	if (cur == nullptr) return nullptr;
	if (cur->data == item) return cur;
	return getData(item, cur->left) != nullptr ? getData(item, cur->left) : getData(item, cur->right);
}

// 判断item是否在树中
template<class T>
bool BTree<T>::Find(T& item) {
	if (this->getData(item, root) == nullptr) return false;
	else return true;
}

// 求树高度
template<class T>
int BTree<T>::Height(BTreeNode<T>* bt) {
	if (bt == nullptr) return 0;
	else {
		int leftH = Height(bt->left);
		int rightH = Height(bt->right);
		return (leftH > rightH) ? leftH + 1 : rightH + 1;
	}
}

// 获取树高度
template<class T>
int BTree<T>::getHeight() {
	return Height(root);
}

// 获取根 
template<class T>
BTreeNode<T>* BTree<T>::getRoot() {
	if (!root) return nullptr;
	else {
		return this->root;
	}
}

// 析构函数
template<class T>
BTree<T>::~BTree<T>() {
	//cout << "调用析构函数" << endl;
	destroyTree(root);
	cout << "报告，这棵树已经销毁完毕!!!" << endl;
}

// 销毁二叉树 
template<class T>
void BTree<T>::destroyTree(BTreeNode<T>* bt) {
	// 后序遍历删除根为subTree的子树；
	if (bt != nullptr) {
		destroyTree(bt->left);    //删除左子树
		destroyTree(bt->right);   //删除右子树
		delete bt; 			      //删除根结点
	}
}

// 前序遍历
template<class T>
void BTree<T>::preOrderTraversal(BTreeNode<T>* cur, vector<int>& vec) {
	if (cur == nullptr)
		return;
	vec.push_back(cur->data);           // 中
	preOrderTraversal(cur->left, vec);  // 左
	preOrderTraversal(cur->right, vec); // 右
}

// 调用前序遍历，返回vector
template<class T>
vector<T> BTree<T>::preOrder() {
	cout << "获取前序遍历数组...." << endl;
	cout << ">>>>";
	vector<T> resVec;
	preOrderTraversal(root, resVec);
	return resVec;
}

// 中序遍历
template<class T>
void BTree<T>::inOrderTraversal(BTreeNode<T>* cur, vector<int>& vec) {
	if (cur == nullptr)
		return;
	inOrderTraversal(cur->left, vec);  // 左
	vec.push_back(cur->data);          // 中
	inOrderTraversal(cur->right, vec); // 右
}

// 调用中序遍历，返回vector
template<class T>
vector<T> BTree<T>::inOrder() {
	cout << "获取中序遍历数组...." << endl;
	cout << ">>>>";
	vector<T> resVec;
	inOrderTraversal(root, resVec);
	return resVec;
}

// 后序遍历
template<class T>
void BTree<T>::postOrderTraversal(BTreeNode<T>* cur, vector<int>& vec) {
	if (cur == nullptr)
		return;
	postOrderTraversal(cur->left, vec);  // 左
	postOrderTraversal(cur->right, vec); // 右
	vec.push_back(cur->data);            // 中
}

// 调用后序遍历，返回vector
template<class T>
vector<T> BTree<T>::postOrder() {
	cout << "获取后序遍历数组...." << endl;
	cout << ">>>>";
	vector<T> resVec;
	postOrderTraversal(root, resVec);
	return resVec;
}

// 层序遍历
template<class T>
void BTree<T>::levelOrderTraversal(BTreeNode<T>* cur, vector<int>& vec) {
	if (cur == nullptr) return;
	queue<BTreeNode<T>*> Queue;
	BTreeNode<T>* p;
	Queue.push(cur); // 根结点入队列
	while (!Queue.empty()) {
		p = Queue.front();
		//cout << p->data << " ";//输出出队结点的数据
		vec.push_back(p->data);
		Queue.pop();
		if (p->left != nullptr) {
			Queue.push(p->left);
		}
		if (p->right != nullptr) {
			Queue.push(p->right);
		}
	}
}

// 调用层序遍历，返回vector
template<class T>
vector<T> BTree<T>::levelOrder() {
	cout << "获取层序遍历数组...." << endl;
	cout << ">>>>";
	vector<T> resVec;
	levelOrderTraversal(root, resVec);
	return resVec;
}

template<class T>
void BTree<T>::CopyTree(BTreeNode<T>* root, BTreeNode<T>*& copyRoot) {
	if (!root) {
		copyRoot = nullptr;
	}
	else {
		copyRoot = new BTreeNode<T>;
		copyRoot->data = root->data;           //复制根节点
		CopyTree(root->left, copyRoot->left);  //递归复制左子树
		CopyTree(root->right, copyRoot->right);//递归复制左子树
	}
}

template<class T>
void BTree<T>::Copy(BTreeNode<T>*& copyRoot) {
	CopyTree(root, copyRoot);
}

template<class T>
void BTree<T>::destroyCopyTree(BTreeNode<T>*& copyRoot) {
	destroyTree(copyRoot);
	cout << "报告，复制二叉树已销毁完毕!!!" << endl;
}

template<class T>
BTreeNode<T>* BTree<T>::FindParent(BTreeNode<T>* root, BTreeNode<T>* node) {

	if (root == nullptr) return nullptr;
	if (root->left == node || root->right == node)
		return root;	     //找到, 返回父结点地址
	BTreeNode <T>* p;
	if ((p = FindParent(root->left, node)) != nullptr)
		return p;	         //递归在左子树中搜索
	else return FindParent(root->right, node);
}

test.cpp

#include "btree.h"
#include "btree.cpp"
//#include <iostream>
//using namespace std;
int main() {
	cout << "-------------------------Start--------------------------" << endl;
	cout << "---------------------创建原始二叉树---------------------" << endl;
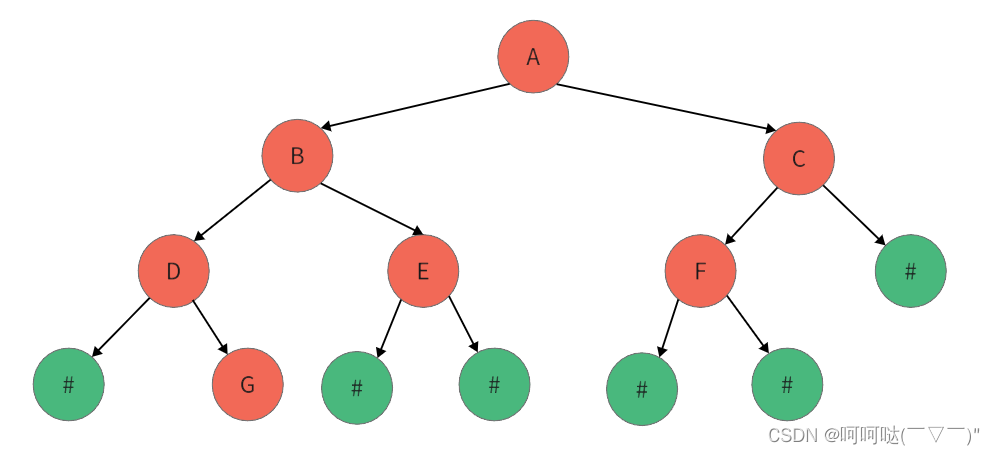
	string str = "ABD#G##E##CF###";
	BTree<int>* T = new BTree<int>(str);
	BTreeNode<int>* root = T->getRoot();
	cout << "这棵树有 " << T->getSize() << " 个结点" << endl;

	int zifu = 'G';
	if (T->Find(zifu)) {
		cout << "这棵树有 " << (char)zifu << " 结点" << endl;
	}
	else {
		cout << "这棵树无 " << (char)zifu << " 结点" << endl;
	}
	BTreeNode<int>* node = T->getData(zifu, root);
	if (node) {
		cout << (char)node->data << endl;
		BTreeNode<int>* nodeParent = T->FindParent(root, node);
		if (!nodeParent) {
			cout << "找不到父亲结点" << endl;
		}
		else {
			cout << "结点 " << (char)zifu << " 的父亲结点是: " << (char)nodeParent->data << " 结点" << endl;
			if (nodeParent->left) cout << "我的左孩子是: " << (char)nodeParent->left->data << endl;
			else cout << "我没有左孩子..." << endl;
			if (nodeParent->right) cout << "我的右孩子是: " << (char)nodeParent->right->data << endl;
			else cout << "我没有右孩子..." << endl;
		}
	}
	cout << "这棵树的高度为: " << T->getHeight() << endl;

	vector<int> vec = T->preOrder();
	for (auto i : vec) {
		cout << (char)i;
	}
	cout << endl;

	vec.clear();
	vec = T->inOrder();
	for (auto i : vec) {
		cout << (char)i;
	}
	cout << endl;

	vec.clear();
	vec = T->postOrder();
	for (auto i : vec) {
		cout << (char)i;
	}
	cout << endl;

	vec.clear();
	vec = T->levelOrder();
	for (auto i : vec) {
		cout << (char)i;
	}
	cout << endl;


	cout << "-----------------------复制二叉树-----------------------" << endl;
	// 复制二叉树
	//vector<int> vec;
	//BTreeNode<int>* root = T->getRoot();
	BTreeNode<int>* copyRoot = new BTreeNode<int>;
	//T->Copy(copyRoot);          // 方法一
	T->CopyTree(root, copyRoot);  // 方法二

	vec.clear();
	cout << "获取前序遍历数组...." << endl;
	cout << ">>>>";
	T->preOrderTraversal(copyRoot, vec);
	for (auto i : vec) {
		cout << (char)i;
	}
	cout << endl;

	vec.clear();
	cout << "获取中序遍历数组...." << endl;
	cout << ">>>>";
	T->inOrderTraversal(copyRoot, vec);
	for (auto i : vec) {
		cout << (char)i;
	}
	cout << endl;

	vec.clear();
	cout << "获取后序遍历数组...." << endl;
	cout << ">>>>";
	T->postOrderTraversal(copyRoot, vec);
	for (auto i : vec) {
		cout << (char)i;
	}
	cout << endl;

	vec.clear();
	cout << "获取层序遍历数组...." << endl;
	cout << ">>>>";
	T->levelOrderTraversal(copyRoot, vec);
	for (auto i : vec) {
		cout << (char)i;
	}
	cout << endl;
	cout << "---------------------销毁复制二叉树---------------------" << endl;
	T->destroyCopyTree(copyRoot);
	cout << "---------------------销毁原始二叉树---------------------" << endl;
	T->~BTree();
	cout << "--------------------------End---------------------------" << endl;
	return 0;
}

>>测试结果

-------------------------Start--------------------------
---------------------创建原始二叉树---------------------
报告：创建一颗二叉树，完成！！！
这棵树有 7 个结点
这棵树有 G 结点
G
结点 G 的父亲结点是: D 结点
我没有左孩子...
我的右孩子是: G
这棵树的高度为: 4
获取前序遍历数组....
>>>>ABDGECF
获取中序遍历数组....
>>>>DGBEAFC
获取后序遍历数组....
>>>>GDEBFCA
获取层序遍历数组....
>>>>ABCDEFG
-----------------------复制二叉树-----------------------
获取前序遍历数组....
>>>>ABDGECF
获取中序遍历数组....
>>>>DGBEAFC
获取后序遍历数组....
>>>>GDEBFCA
获取层序遍历数组....
>>>>ABCDEFG
---------------------销毁复制二叉树---------------------
报告，复制二叉树已销毁完毕!!!
---------------------销毁原始二叉树---------------------
报告，这棵树已经销毁完毕!!!
--------------------------End---------------------------