💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码、数据、文章讲解
💥1 概述
文献来源:

在这项工作中,我们展示了物理原理 - 例如对称性, 不变性和守恒定律 -- 可以集成到动态模式中 分解(DMD)。DMD是一种广泛使用的数据分析技术,它提取 来自高维测量的低秩模态结构和动力学。 但是,DMD 经常生成对噪声敏感的模型,无法 泛化在训练数据之外,违反基本物理定律。我们 物理信息DMD(piDMD)优化,可以表述为: Procrusts问题,将可接受的模型族限制为矩阵 尊重系统物理结构的歧管。我们专注于五个 基本物理原理——守恒、自伴随、 局部化、因果关系和移位不变性——并推导出几种闭合形式 解决方案和有效的算法,用于相应的piDMD优化。 由于自由度较低,piDMD模型不易过度拟合, 需要较少的训练数据,并且通常计算成本较低 比标准 DMD 模型构建。我们在一系列具有挑战性的领域展示了piDMD 物理科学中的问题,包括能量保存流体流动, 行波系统,薛定谔方程,溶质 平流扩散,具有因果动力学和三维的系统 过渡通道流。在每种情况下,piDMD的表现都明显优于piDMD 频谱识别、状态预测和 估计最佳强迫和响应。
基于物理场的动态模式分解(piDMD)是一种用于分析和预测动态系统行为的方法。它结合了动态模式分解(DMD)和物理场的信息,能够提供更准确和可解释的结果。
DMD是一种基于线性动力学系统的模型,通过分析系统的瞬时模态和频率来描述系统的行为。然而,DMD只能提供系统的近似模型,对于非线性系统和包含噪声的数据,其结果可能不准确。
piDMD通过将物理场的信息引入DMD模型中,能够更好地捕捉系统的非线性行为和噪声。具体来说,piDMD将物理场的信息作为约束条件加入到DMD模型中,通过优化算法来求解最优的模型参数。这样可以更好地拟合系统的动态行为,并提供更准确的预测结果。
piDMD的研究可以应用在许多领域,如气象预测、流体力学、结构动力学等。它可以帮助科学家和工程师更好地理解和预测复杂系统的行为,从而优化系统设计和控制策略。
总之,基于物理场的动态模式分解是一种结合了DMD和物理场信息的方法,能够提供更准确和可解释的动态系统分析和预测结果。它在许多领域具有广泛的应用前景。


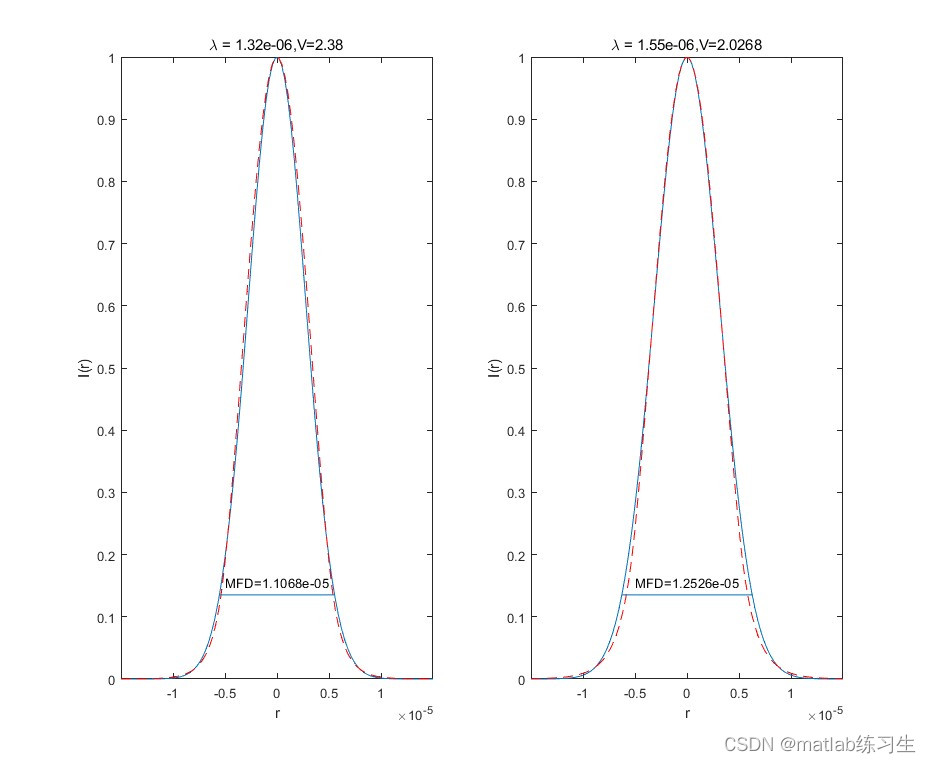
📚2 运行结果

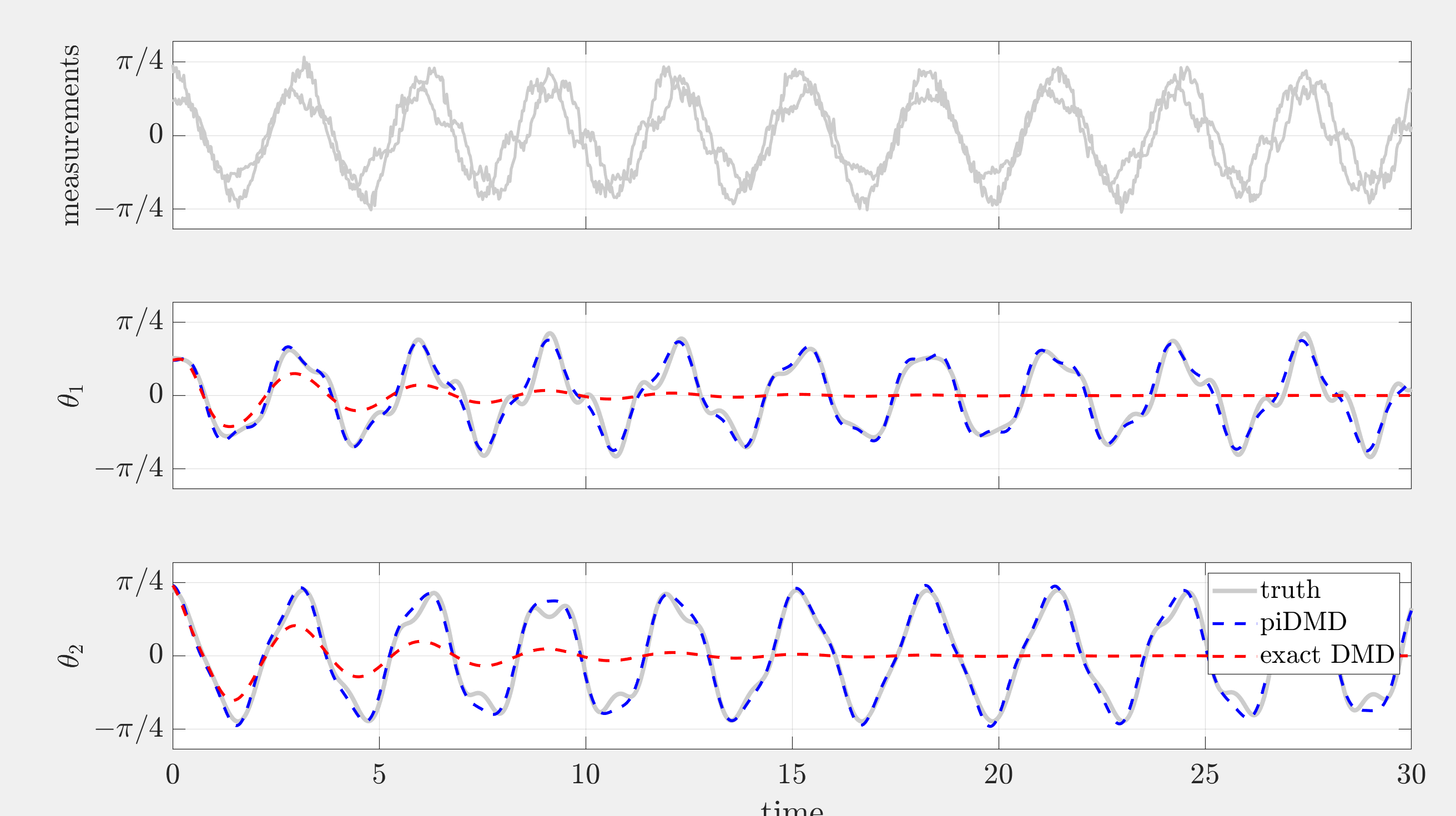



部分代码:
%% Plot some results
FS = 'FontSize'; IN = 'Interpreter'; LT = 'Latex'; MS = 'MarkerSize'; LW = 'LineWidth';
figure(1)
clf
plot(exp(1i*linspace(0,2*pi)),'--','Color',[1 1 1]*.5,LW,2)
hold on
p2 = plot((exVals)+1i*eps,'r^',LW,2,MS,10);
p3 = plot((piVals)+1i*eps,'bx',LW,2,MS,10);
p4 = plot((trueVals)+1i*eps,'o','Color',.5*[1 1 1],LW,2,MS,10);
grid on; axis equal; hold off
axis(1.3*[-1,1,-1,1])
legend([p2,p3,p4],{'exact DMD','piDMD','truth'},FS,15,IN,LT)
title('Spectrum of linear operator',FS,20,IN,LT)
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。