玩转线性代数(22)向量组与线性组合、线性表示的笔记，相关证明以及例子见原文

向量方程

对线性方程组$Ax=b$，将系数矩阵A按列分块，即$A=(a_1,a_2,...,a_n)$，则$Ac=b$可以写成如下形式：
$$x_1{a}_1+x_2{a}_2+...+x_n{a}_n=b$$
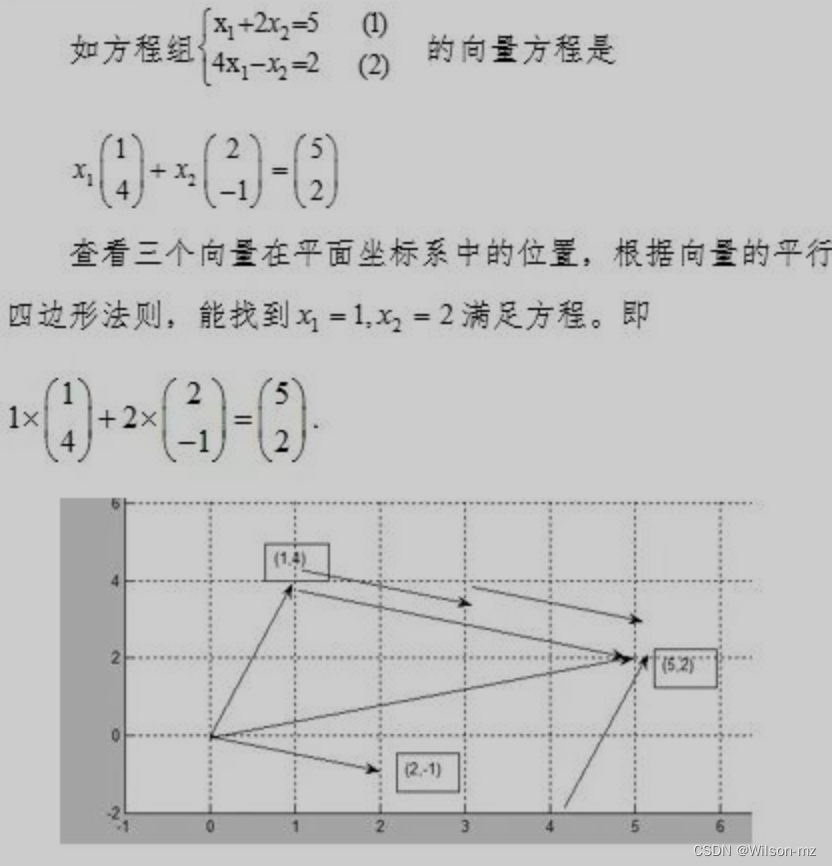
将上式称为向量方程

从向量方程可以直观地查看线性方程组的几何意义：

向量与向量组

向量

定义：n个有次序有数$a_1,a_2,...a_n$所组成的数组称为n维向量，其中$a_i$称为向量的第i个分量
分类：按元素所在数域分为实向量、复向量；按组织形式可以分为行向量与列向量。
表示：一般用小写字母表示，如$a,b,c...$
运算：向量也是矩阵，按矩阵的运算规律进行运算。

向量组

定义：若干个同维数的行向量或列向量组成的集合叫向量组。
表示方法：向量组A用$A:a_1,a_2,...,a_n$表示
分类：有限和无限向量组
（1）A：$a_1,2a_2,...n{a}_n,...$含有无限个向量
（2）$Ax=0$当$|A|=0$时的解向量组成的向量组含有无限个向量
（3）m行n列矩阵A的行向量组或列向量组含有有限个向量

线性组合与线性表示

线性组合

定义：给定向量组$A:a_1,a_2,...,a_n$，对于任何一组实数$k_1,k_2,...,k_n$，表达式
$$k_1{a}_1+k_2{a}_2+...+k_n{a}_n$$
称为向量组A的一个线性组合，$k_1,k_2,...,k_n$称为这个线性组合的系数

线性表示

向量方程是一个等式，就是研究向量组的线性组合是否等于某个向量的问题
定义：向量b能由向量组A线性表示（多表单）：给定向量组$A:a_1,a_2,...,a_n$和向量b，若存在一组数$k_1,k_2,...,k_n$使
$$k_1{a}_1+k_2{a}_2+...+k_n{a}_n=b$$
则称向量b是向量组A的线性组合，又称向量b能由向量组A线性表示（或线性表出）

定理

向量b能由向量组$A:a_1,a_2,...,a_n$线性表示的充分必要条件是矩阵$A=(a_1,a_2,...,a_n)$与矩阵$B=(a_1,a_2,...,a_n,b)$的秩相等，即$R(A)=R(A,b)$。
根据定理马上得到以下结论：
（1）b能由向量组$A:a_1,a_2,...,a_n$唯一线性表示的充分必要条件是线性方程组$a_1{x}_1+a_2{x}_2+...+a_n{x}_n=b$有唯一解，即$R(A)=R(B)=n$;
（2）b能由向量组$A:a_1,a_2,...,a_n$线性表示且表示不唯一的充分必要条件是线性方程组$a_1{x}_1+a_2{x}_2+...+a_n{x}_n=b$有无穷多解，即$R(A)=R(B)<n$;
（3）b不能由向量组$A:a_1,a_2,...,a_n$线性表示的充分必要条件是线性方程组$a_1{x}_1+a_2{x}_2+...+a_n{x}_n=b$无解，即$R(A)<R(B)$

定义 多表多（单向）

设有两向量组
$A:a_1,a_2,...,a_n$, $B:b_1,b_2,...,b_l$
若向量组B中的每一个向量都能由向量组A线性表示，则称向量组B能由向量组A线性表示。
问题：如何判断向量组B能由向量组A线性表示？
分析：向量组B能由向量组A线性表示$\iff$
$b_1=\left(\begin{array}{cccc}{a}_1& a_2& \cdots & a_n\end{array}\right)\left(\begin{array}{c}{k}_{11}\\ k_{21}\\ ⋮\\ k_{n1}\end{array}\right),\cdots ,b_l=\left(\begin{array}{cccc}{a}_1& a_2& \cdots & a_n\end{array}\right)\left(\begin{array}{c}{k}_{1l}\\ k_{2l}\\ ⋮\\ k_{nl}\end{array}\right)\iff B=AK\iff B=Ax$有解$\iff R(A)=R(A,B)$（此时x为矩阵）

定理

向量组B由向量组A线性表示的充要条件是$R(A)=R(A,B)$

推论

若向量组B能由向量组A线性表示，则$A=(a_1,a_2,...,a_n)$与 $B=(a_1,a_2,...,a_n,b_1,b_2,...,b_l)$的秩的关系为$R(B)\le R(A)$.
例：设有n维向量组$A:a_1,a_2,...,a_n$和n阶单位矩阵E的列向量组$(e_1,e_2,\cdots ,e_n)$，试证明：$E:e_1,e_2,\cdots ,e_n$能由$A:a_1,a_2,...,a_n$线性表示的充要条件是$R(A)=n$.
证明：必要性：首先，$R(A)\le n$(n维)；又根据推论，$n=R(E)\le R(A)$，故$R(A)=n$;
充分性：只证$R(A)=R(A,E)$，显然$n=R(E)\le R(A,E)\le n(维数)$.
故：$R(A,E)=R(A)=R(E)$.

定义 等价（多表多：双向）

定义：设有两个向量组$A:a_1,a_2,...,a_n$，$B:b_1,b_2,...,b_l$，若向量组A与B能互相线性表示，则称这两个向量组等价，记做$A\sim B$
note: 前面讲过矩阵等价，行等价，列等价，等价具备自反性、对称性和传递性。向量组的等价也满足这三种性质。
判定：向量组$A:a_1,a_2,...,a_n$与$B:b_1,b_2,...,b_l$等价$\iff R(A)=R(B)=R(A,B)$

知识回顾

线性方程组解的判断要通过矩阵的秩，求解需要矩阵的初等行变换、向量组的线性表示也需要矩阵的秩来判断，如果我们把涉及到矩阵的相关操作称为矩阵语言，把方程的相关描述称为代数语言，将向量的关系称为几何语言，那么这三者之间可以相互转化，并最终转化为矩阵语言来解决问题。
向量组$B:b_1,b_2,...,b_l$能由$A:a_1,a_2,...,a_n$线性表示$\iff$存在矩阵K，使B=AK$\iff$方程$AX=B$有解$\iff R(A)=R(A,B)$。
把线性方程组写成矩阵形式，通过矩阵的运算求得它的解，还用矩阵的语言给出了线性方程组有解、有唯一解的充要条件；将向量组的问题表述成矩阵形式，通过矩阵的运算得出结果，然后把矩阵的形式的结果“翻译”成几何问题的结论。这种用矩阵来表述问题，并通过矩阵的运算解决问题的方法，通常叫做矩阵方法，正是线性代数的基本方法。