题目链接
https://leetcode.cn/problems/longest-palindromic-subsequence/description/?utm_source=LCUS&utm_medium=ip_redirect&utm_campaign=transfer2china
目录
题目描述：
暴力递归：
动态规划：
题目描述：
给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。
示例 1：
输入：s = "bbbab" 输出：4 解释：一个可能的最长回文子序列为 "bbbb" 。示例 2：
输入：s = "cbbd" 输出：2 解释：一个可能的最长回文子序列为 "bb" 。提示：
1 <= s.length <= 1000s仅由小写英文字母组成
这道题的知识点是动态规划，可是如果直接从动态规划讲可能有点不容易理解。
所以本篇文章就是从暴力递归到动态规划。
从题目中我们可以得出：本题找的是可以不连续的回文子串然后返回其最大序列的长度。
也就是说：
a2b42a
的最长回文子序列为：a2b2a或a242a 这两个都可以因为它们返回的都是5
暴力递归：
我们先写一个可以返回最长的回文子序列长度的函数：
//主函数
public int longestPalindromeSubseq(String s) {
char[] str = s.toCharArray();
return maxString(str, 0, str.length-1);
}
//假设该函数可以返回最长回文子序列的长度
public static int maxString(char[] str, int l, int r) {}我们写的 maxString() 方法可以返回 str 字符串[l, r]区间的最长回文子序列的长度 。
通过分析可以得出以下结论：
两种特殊情况：
- 首先我们可以得到当 l 和 r 相等就证明此时只有一个字符那么它的返回值就是 1 。
- 如果传入的数组只有两个字符即 l + 1 == r 那么此时如果这两个字符相等就返回 2 ，如果不相等就返回 1 。
普遍情况：
- 两边的字符都不存在于最长的回文子序列中。例：a1221b -> 1221;
- 右边的字符不存在在于最长的回文子序列中。例：1221b -> 1221;
- 左边的字符不存在在于最长的回文子序列中。例：a1221 -> 1221;
- 两边的字符都存在于最长的回文子序列中。例：1w221 -> 1221。
此时代码就可以这样写：
//主函数
public int longestPalindromeSubseq(String s) {
char[] str = s.toCharArray();
return maxString(str, 0, str.length-1);
}
//假设该函数可以返回最长回文子序列的长度
public static int maxString(char[] str, int l, int r) {
//先判断两种特殊情况
if (l == r){
return 1;
}
if (l + 1 == r){
return str[l] == str[r] ? 2 : 1;
}
//余下的四种情况
int a1 = maxString(str, l + 1, r - 1);
int a2 = maxString(str, l, r - 1);
int a3 = maxString(str, l + 1, r);
int a4 = str[l] == str[r] ? 2 + maxString(str, l + 1, r - 1) : 0;
//因为题目要求返回最长序列长度 所以需要返回这四个的最大值
return Math.max(Math.max(a1, a2), Math.max(a3, a4));
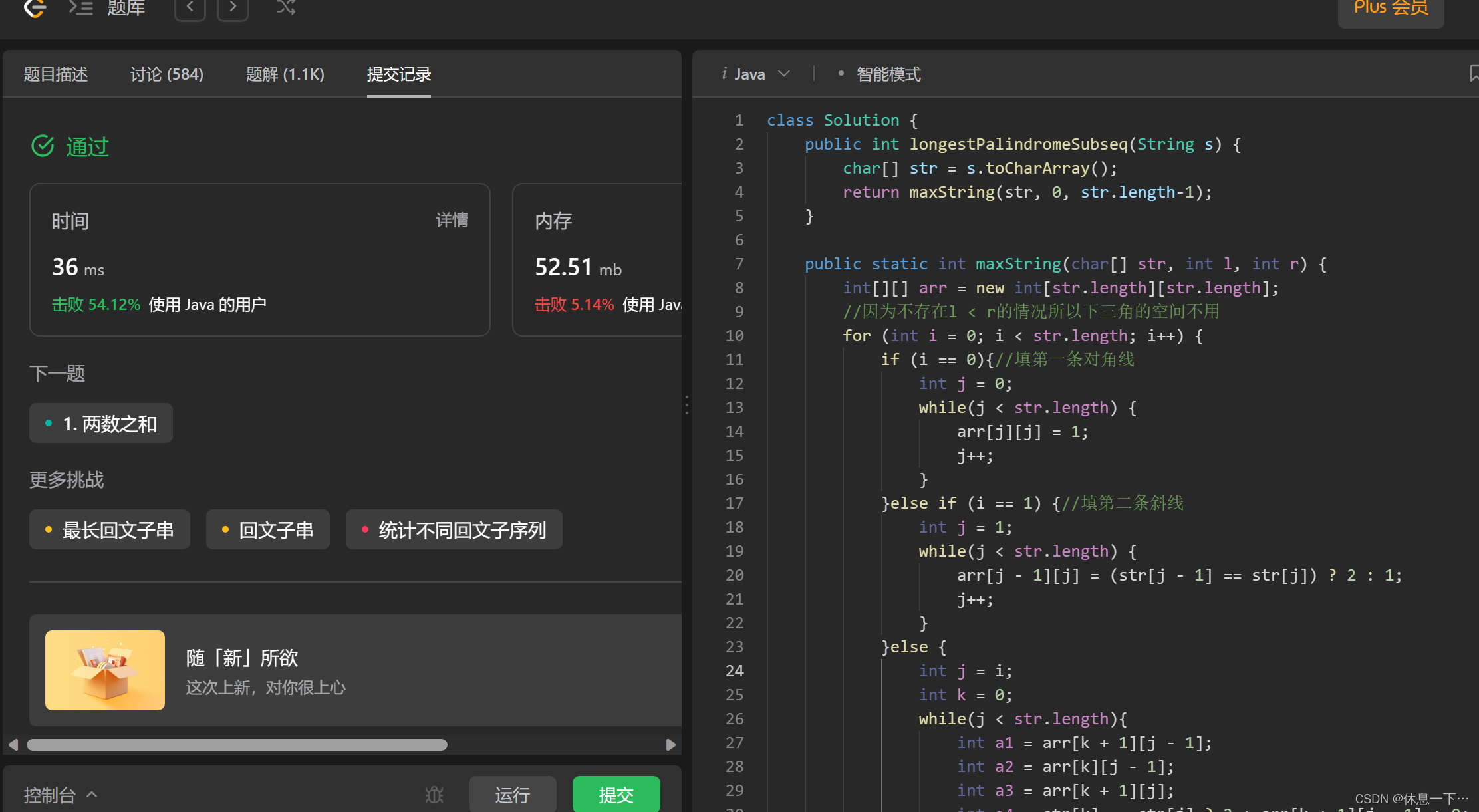
}此时我们可以提交以下：
虽然没通过但是从它的报错信息可以看出，我们的思路是没问题的。
动态规划：
我们有了递归版本后就可以根据它来写出动态规划版本了。
因为在maxString() 方法中只有 l 和 r 是变量，而它们两个的取值范围都是 [0，str.length - 1]
此时我们就可以通过创建一个二维数组将 l 和 r 所有情况都列举出来然后返回数组[0，str.length - 1] 下标的值就可以得出答案了。
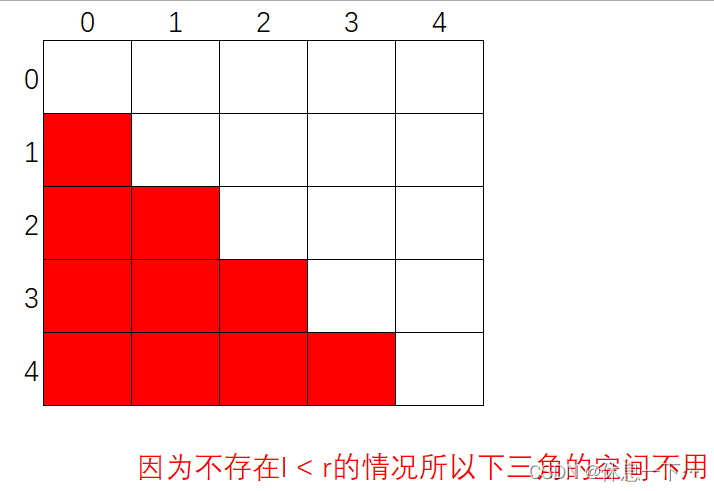
我们先假设长度只有 5 ，那么我们就可以创建如下的二维数组 l 行，r 列
public static int maxString(char[] str, int l, int r) {
int[][] arr = new int[str.length][str.length];
} 
接下来的填表阶段就可以根据递归函数直接填（以“a1221”为例子）：
此时 [0， 4] 位置的值就是最终答案。
根据每个位置的关系就将递归优化成：
public static int maxString(char[] str, int l, int r) {
int[][] arr = new int[str.length][str.length];
//因为不存在l < r的情况所以下三角的空间不用
for (int i = 0; i < str.length; i++) {
if (i == 0){//填第一条对角线
int j = 0;
while(j < str.length) {
arr[j][j] = 1;
j++;
}
}else if (i == 1) {//填第二条斜线
int j = 1;
while(j < str.length) {
arr[j - 1][j] = (str[j - 1] == str[j]) ? 2 : 1;
j++;
}
}else {//其他
int j = i;
int k = 0;
while(j < str.length){
int a1 = arr[k + 1][j - 1];
int a2 = arr[k][j - 1];
int a3 = arr[k + 1][j];
int a4 = str[k] == str[j] ? 2 + arr[k + 1][j - 1] : 0;
arr[k][j] = Math.max(Math.max(a1, a2), Math.max(a3, a4));
j++;
k++;
}
}
}
return arr[0][str.length-1];
}此时再提交就过了。
