✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。
🍎个人主页:小嗷犬的个人主页
🍊个人网站:小嗷犬的技术小站
🥭个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。
本文目录
- 堆简介
- 堆的分类
- 二叉堆
- 结构
- 过程
- 插入操作
- 删除操作
- 增加某个点的权值
- 实现
- 建堆
- 方法一:使用 decreasekey(即,向上调整)
- 方法二:使用向下调整
- 配对堆
- 引入
- 定义
- 过程
- 查询最小值
- 合并
- 插入
- 删除最小值
- 减小一个元素的值
- 复杂度分析
- 左偏树
- 什么是左偏树?
- dist 的定义和性质
- 左偏树的定义和性质
- 核心操作:合并(merge)
- 左偏树的其它操作
- 插入节点
- 删除根
- 删除任意节点
- 做法
- 复杂度分析
- 整个堆加上/减去一个值、乘上一个正数
- 随机合并
堆简介
堆是一棵树,其每个节点都有一个键值,且每个节点的键值都大于等于/小于等于其父亲的键值。
每个节点的键值都大于等于其父亲键值的堆叫做小根堆,否则叫做大根堆。STL 中的 priority_queue 其实就是一个大根堆。
(小根)堆主要支持的操作有:插入一个数、查询最小值、删除最小值、合并两个堆、减小一个元素的值。
一些功能强大的堆(可并堆)还能(高效地)支持 merge 等操作。
一些功能更强大的堆还支持可持久化,也就是对任意历史版本进行查询或者操作,产生新的版本。
堆的分类
| 操作 \ 数据结构 | 配对堆 | 二叉堆 | 左偏树 | 二项堆 | 斐波那契堆 |
|---|---|---|---|---|---|
| 插入(insert) | O ( 1 ) O(1) O(1) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) | O ( 1 ) O(1) O(1) | O ( 1 ) O(1) O(1) |
| 查询最小值(find-min) | O ( 1 ) O(1) O(1) | O ( 1 ) O(1) O(1) | O ( 1 ) O(1) O(1) | O ( log n ) O(\log n) O(logn) | O ( 1 ) O(1) O(1) |
| 删除最小值(delete-min) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) |
| 合并 (merge) | O ( 1 ) O(1) O(1) | O ( n ) O(n) O(n) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) | O ( 1 ) O(1) O(1) |
| 减小一个元素的值 (decrease-key) | o ( log n ) o(\log n) o(logn)(下界 Ω ( log log n ) \Omega(\log \log n) Ω(loglogn),上界 O ( 2 2 log log n ) O(2^{2\sqrt{\log \log n}}) O(22loglogn)) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) | O ( 1 ) O(1) O(1) |
| 是否支持可持久化 | × \times × | ✓ \checkmark ✓ | ✓ \checkmark ✓ | ✓ \checkmark ✓ | × \times × |
习惯上,不加限定提到「堆」时往往都指二叉堆。
二叉堆
结构
从二叉堆的结构说起,它是一棵二叉树,并且是完全二叉树,每个结点中存有一个元素(或者说,有个权值)。
堆性质:父亲的权值不小于儿子的权值(大根堆)。同样的,我们可以定义小根堆。本章以大根堆为例。
由堆性质,树根存的是最大值。
过程
插入操作
插入操作是指向二叉堆中插入一个元素,要保证插入后也是一棵完全二叉树。
最简单的方法就是,最下一层最右边的叶子之后插入。
如果最下一层已满,就新增一层。
插入之后可能会不满足堆性质?
向上调整: 如果这个结点的权值大于它父亲的权值,就交换,重复此过程直到不满足或者到根。
可以证明,插入之后向上调整后,没有其他结点会不满足堆性质。
向上调整的时间复杂度是 O ( log n ) O(\log n) O(logn) 的。

删除操作
删除操作指删除堆中最大的元素,即删除根结点。
但是如果直接删除,则变成了两个堆,难以处理。
所以不妨考虑插入操作的逆过程,设法将根结点移到最后一个结点,然后直接删掉。
然而实际上不好做,我们通常采用的方法是,把根结点和最后一个结点直接交换。
于是直接删掉(在最后一个结点处的)根结点,但是新的根结点可能不满足堆性质……
向下调整: 在该结点的儿子中,找一个最大的,与该结点交换,重复此过程直到底层。
可以证明,删除并向下调整后,没有其他结点不满足堆性质。
时间复杂度 O ( log n ) O(\log n) O(logn)。
增加某个点的权值
很显然,直接修改后,向上调整一次即可,时间复杂度为 O ( log n ) O(\log n) O(logn)。
实现
我们发现,上面介绍的几种操作主要依赖于两个核心:向上调整和向下调整。
考虑使用一个序列 h h h 来表示堆。 h i h_i hi 的两个儿子分别是 h 2 i h_{2i} h2i 和 h 2 i + 1 h_{2i+1} h2i+1, 1 1 1 是根结点:
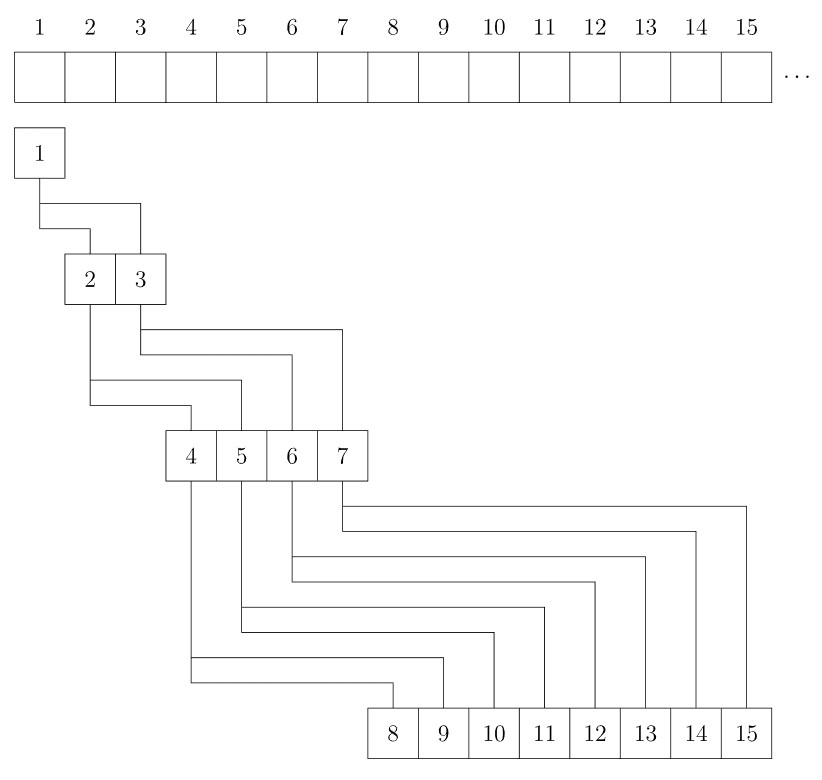
参考代码:
void up(int x)
{
while (x > 1 && h[x] > h[x / 2])
{
std::swap(h[x], h[x / 2]);
x /= 2;
}
}
void down(int x)
{
while (x * 2 <= n)
{
t = x * 2;
if (t + 1 <= n && h[t + 1] > h[t])
t++;
if (h[t] <= h[x])
break;
std::swap(h[x], h[t]);
x = t;
}
}
建堆
考虑这么一个问题,从一个空的堆开始,插入 n n n 个元素,不在乎顺序。
直接一个一个插入需要 O ( n log n ) O(n \log n) O(nlogn) 的时间,有没有更好的方法?
方法一:使用 decreasekey(即,向上调整)
从根开始,按 BFS 序进行。
void build_heap_1()
{
for (i = 1; i <= n; i++)
up(i);
}
为啥这么做:对于第 k k k 层的结点,向上调整的复杂度为 O ( k ) O(k) O(k) 而不是 O ( log n ) O(\log n) O(logn)。
总复杂度: log 1 + log 2 + ⋯ + log n = Θ ( n log n ) \log 1 + \log 2 + \cdots + \log n = \Theta(n \log n) log1+log2+⋯+logn=Θ(nlogn)。
方法二:使用向下调整
这时换一种思路,从叶子开始,逐个向下调整。
void build_heap_2()
{
for (i = n; i >= 1; i--)
down(i);
}
换一种理解方法,每次「合并」两个已经调整好的堆,这说明了正确性。
注意到向下调整的复杂度,为 O ( log n − k ) O(\log n - k) O(logn−k),另外注意到叶节点无需调整,因此可从序列约 n / 2 n/2 n/2 的位置开始调整,可减少部分常数但不影响复杂度。
总复杂度 = n log n − log 1 − log 2 − ⋯ − log n ≤ n log n − 0 × 2 0 − 1 × 2 1 − ⋯ − ( log n − 1 ) × n 2 = n log n − ( n − 1 ) − ( n − 2 ) − ( n − 4 ) − ⋯ − ( n − n 2 ) = n log n − n log n + 1 + 2 + 4 + ⋯ + n 2 = n − 1 = O ( n ) \begin{aligned} \text{总复杂度} & = n \log n - \log 1 - \log 2 - \cdots - \log n \\ & \leq n \log n - 0 \times 2^0 - 1 \times 2^1 -\cdots - (\log n - 1) \times \frac{n}{2} \\\ & = n \log n - (n-1) - (n-2) - (n-4) - \cdots - (n-\frac{n}{2}) \\ & = n \log n - n \log n + 1 + 2 + 4 + \cdots + \frac{n}{2} \\ & = n - 1 \\ & = O(n) \end{aligned} 总复杂度 =nlogn−log1−log2−⋯−logn≤nlogn−0×20−1×21−⋯−(logn−1)×2n=nlogn−(n−1)−(n−2)−(n−4)−⋯−(n−2n)=nlogn−nlogn+1+2+4+⋯+2n=n−1=O(n)
之所以能 O ( n ) O(n) O(n) 建堆,是因为堆性质很弱,二叉堆并不是唯一的。
配对堆
引入
配对堆是一个支持插入,查询/删除最小值,合并,修改元素等操作的数据结构,是一种可并堆。有速度快和结构简单的优势,但由于其为基于势能分析的均摊复杂度,无法可持久化。
定义
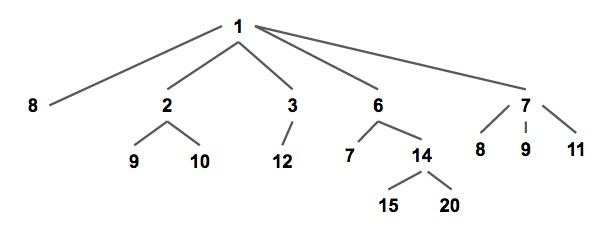
配对堆是一棵满足堆性质的带权多叉树(如下图),即每个节点的权值都小于或等于他的所有儿子(以小根堆为例,下同)。
通常我们使用儿子 - 兄弟表示法储存一个配对堆(如下图),一个节点的所有儿子节点形成一个单向链表。每个节点储存第一个儿子的指针,即链表的头节点;和他的右兄弟的指针。
这种方式便于实现配对堆,也将方便复杂度分析。
struct Node
{
T v; // T为权值类型
Node *child, *sibling;
// child 指向该节点第一个儿子,sibling 指向该节点的下一个兄弟。
// 若该节点没有儿子/下个兄弟则指针指向 nullptr。
};
从定义可以发现,和其他常见的堆结构相比,配对堆不维护任何额外的树大小,深度,排名等信息(二叉堆也不维护额外信息,但它是通过维持一个严格的完全二叉树结构来保证操作的复杂度),且任何一个满足堆性质的树都是一个合法的配对堆,这样简单又高度灵活的数据结构奠定了配对堆在实践中优秀效率的基础;作为对比,斐波那契堆糟糕的常数就是因为它需要维护很多额外的信息。
配对堆通过一套精心设计的操作顺序来保证它的总复杂度,原论文1将其称为「一种自调整的堆(Self Adjusting Heap)」。在这方面和 Splay 树(在原论文中被称作「Self Adjusting Binary Tree」)颇有相似之处。
过程
查询最小值
从配对堆的定义可看出,配对堆的根节点的权值一定最小,直接返回根节点即可。
合并
合并两个配对堆的操作很简单,首先令两个根节点较小的一个为新的根节点,然后将较大的根节点作为它的儿子插入进去。(见下图)

需要注意的是,一个节点的儿子链表是按插入时间排序的,即最右边的节点最早成为父节点的儿子,最左边的节点最近成为父节点的儿子。
Node *meld(Node *x, Node *y)
{
// 若有一个为空则直接返回另一个
if (x == nullptr)
return y;
if (y == nullptr)
return x;
if (x->v > y->v)
std::swap(x, y); // swap后x为权值小的堆,y为权值大的堆
// 将y设为x的儿子
y->sibling = x->child;
x->child = y;
return x; // 新的根节点为 x
}
插入
合并都有了,插入就直接把新元素视为一个新的配对堆和原堆合并就行了。
删除最小值
首先要提及的一点是,上文的几个操作都十分偷懒,完全没有对数据结构进行维护,所以我们需要小心设计删除最小值的操作,来保证总复杂度不出问题。
根节点即为最小值,所以要删除的是根节点。考虑拿掉根节点之后会发生什么:根节点原来的所有儿子构成了一片森林;而配对堆应当是一棵树,所以我们需要通过某种顺序把这些儿子全部合并起来。
一个很自然的想法是使用 meld 函数把儿子们从左到右挨个并在一起,这样做的话正确性是显然的,但是会导致单次操作复杂度退化到
O
(
n
)
O(n)
O(n)。
为了保证总的均摊复杂度,需要使用一个「两步走」的合并方法:
- 把儿子们两两配成一对,用
meld操作把被配成同一对的两个儿子合并到一起(见下图 1), - 将新产生的堆 从右往左(即老的儿子到新的儿子的方向)挨个合并在一起(见下图 2)。
先实现一个辅助函数 merges,作用是合并一个节点的所有兄弟。
Node *merges(Node *x)
{
if (x == nullptr || x->sibling == nullptr)
return x; // 如果该树为空或他没有下一个兄弟,就不需要合并了,return。
Node *y = x->sibling; // y 为 x 的下一个兄弟
Node *c = y->sibling; // c 是再下一个兄弟
x->sibling = y->sibling = nullptr; // 拆散
return meld(merges(c), meld(x, y)); // 核心部分
}
最后一句话是该函数的核心,这句话分三部分:
meld(x,y)「配对」了 x 和 y。merges(c)递归合并 c 和他的兄弟们。- 将上面 2 个操作产生的 2 个新树合并。
需要注意到的是,上文提到了第二步时的合并方向是有要求的(从右往左合并),该递归函数的实现已保证了这个顺序,如果读者需要自行实现迭代版本的话请务必注意保证该顺序,否则复杂度将失去保证。
有了 merges 函数,delete-min 操作就显然了。
Node *delete_min(Node *x)
{
Node *t = merges(x->child);
delete x; // 如果需要内存回收
return t;
}
减小一个元素的值
要实现这个操作,需要给节点添加一个「父」指针,当节点有左兄弟时,其指向左兄弟而非实际的父节点;否则,指向其父节点。
首先节点的定义修改为:
struct Node
{
LL v;
int id;
Node *child, *sibling;
Node *father; // 新增:父指针,若该节点为根节点则指向空节点 nullptr
};
meld 操作修改为:
Node *meld(Node *x, Node *y)
{
if (x == nullptr)
return y;
if (y == nullptr)
return x;
if (x->v > y->v)
std::swap(x, y);
if (x->child != nullptr)
{ // 新增:维护父指针
x->child->father = y;
}
y->sibling = x->child;
y->father = x; // 新增:维护父指针
x->child = y;
return x;
}
merges 操作修改为:
Node *merges(Node *x)
{
if (x == nullptr)
return nullptr;
x->father = nullptr; // 新增:维护父指针
if (x->sibling == nullptr)
return x;
Node *y = x->sibling, *c = y->sibling;
y->father = nullptr; // 新增:维护父指针
x->sibling = y->sibling = nullptr;
return meld(merges(c), meld(x, y));
}
现在我们来考虑如何实现 decrease-key 操作。
首先我们发现,当我们减少节点 x 的权值之后,以 x 为根的子树仍然满足配对堆性质,但 x 的父亲和 x 之间可能不再满足堆性质。
因此我们把整棵以 x 为根的子树剖出来,现在两棵树都符合配对堆性质了,然后把他们合并起来,就完成了全部操作。
// root为堆的根,x为要操作的节点,v为新的权值,调用时需保证 v <= x->v
// 返回值为新的根节点
Node *decrease_key(Node *root, Node *x, LL v)
{
x->v = v; // 更新权值
if (x == root)
return x; // 如果 x 为根,则直接返回
// 把x从fa的子节点中剖出去,这里要分x的位置讨论一下。
if (x->father->child == x)
x->father->child = x->sibling;
else
x->father->sibling = x->sibling;
if (x->sibling != nullptr)
x->sibling->father = x->father;
x->sibling = nullptr;
x->father = nullptr;
return meld(root, x); // 重新合并 x 和根节点
}
复杂度分析
配对堆结构与实现简单,但时间复杂度分析并不容易。
原论文1仅将复杂度分析到 meld 和 delete-min 操作均为均摊
O
(
log
n
)
O(\log n)
O(logn),但提出猜想认为其各操作都有和斐波那契堆相同的复杂度。
遗憾的是,后续发现,不维护额外信息的配对堆,在特定的操作序列下,decrease-key 操作的均摊复杂度下界至少为
Ω
(
log
log
n
)
\Omega (\log \log n)
Ω(loglogn)2。
目前对复杂度上界比较好的估计有,Iacono 的
O
(
1
)
O(1)
O(1) meld,
O
(
log
n
)
O(\log n)
O(logn) decrease-key3;Pettie 的
O
(
2
2
log
log
n
)
O(2^{2 \sqrt{\log \log n}})
O(22loglogn) meld 和 decrease-key4。需要注意的是,前述复杂度均为均摊复杂度,因此不能对各结果分别取最小值。
左偏树
什么是左偏树?
左偏树 与 配对堆 一样,是一种 可并堆,具有堆的性质,并且可以快速合并。
dist 的定义和性质
对于一棵二叉树,我们定义 外节点 为左儿子或右儿子为空的节点,定义一个外节点的 d i s t \mathrm{dist} dist 为 1 1 1,一个不是外节点的节点 d i s t \mathrm{dist} dist 为其到子树中最近的外节点的距离加一。空节点的 d i s t \mathrm{dist} dist 为 0 0 0。
注:很多其它教程中定义的 d i s t \mathrm{dist} dist 都是本文中的 d i s t \mathrm{dist} dist 减去 1 1 1,本文这样定义是因为代码写起来方便。
一棵有 n n n 个节点的二叉树,根的 d i s t \mathrm{dist} dist 不超过 ⌈ log ( n + 1 ) ⌉ \left\lceil\log (n+1)\right\rceil ⌈log(n+1)⌉,因为一棵根的 d i s t \mathrm{dist} dist 为 x x x 的二叉树至少有 x − 1 x-1 x−1 层是满二叉树,那么就至少有 2 x − 1 2^x-1 2x−1 个节点。注意这个性质是所有二叉树都具有的,并不是左偏树所特有的。
左偏树的定义和性质
左偏树是一棵二叉树,它不仅具有堆的性质,并且是「左偏」的:每个节点左儿子的 d i s t \mathrm{dist} dist 都大于等于右儿子的 d i s t \mathrm{dist} dist。
因此,左偏树每个节点的 d i s t \mathrm{dist} dist 都等于其右儿子的 d i s t \mathrm{dist} dist 加一。
需要注意的是, d i s t \mathrm{dist} dist 不是深度,左偏树的深度没有保证,一条向左的链也是左偏树。
核心操作:合并(merge)
合并两个堆时,由于要满足堆性质,先取值较小(为了方便,本文讨论小根堆)的那个根作为合并后堆的根节点,然后将这个根的左儿子作为合并后堆的左儿子,递归地合并其右儿子与另一个堆,作为合并后的堆的右儿子。为了满足左偏性质,合并后若左儿子的 d i s t \mathrm{dist} dist 小于右儿子的 d i s t \mathrm{dist} dist,就交换两个儿子。
参考代码:
int merge(int x, int y)
{
if (!x || !y)
return x | y; // 若一个堆为空则返回另一个堆
if (t[x].val > t[y].val)
swap(x, y); // 取值较小的作为根
t[x].rs = merge(t[x].rs, y); // 递归合并右儿子与另一个堆
if (t[t[x].rs].d > t[t[x].ls].d)
swap(t[x].ls, t[x].rs); // 若不满足左偏性质则交换左右儿子
t[x].d = t[t[x].rs].d + 1; // 更新dist
return x;
}
由于左偏性质,每递归一层,其中一个堆根节点的 d i s t \mathrm{dist} dist 就会减小 1 1 1,而「一棵有 n n n 个节点的二叉树,根的 d i s t \mathrm{dist} dist 不超过 ⌈ log ( n + 1 ) ⌉ \left\lceil\log (n+1)\right\rceil ⌈log(n+1)⌉」,所以合并两个大小分别为 n n n 和 m m m 的堆复杂度是 O ( log n + log m ) O(\log n+\log m) O(logn+logm)。
左偏树还有一种无需交换左右儿子的写法:将 d i s t \mathrm{dist} dist 较大的儿子视作左儿子, d i s t \mathrm{dist} dist 较小的儿子视作右儿子:
int &rs(int x) { return t[x].ch[t[t[x].ch[1]].d < t[t[x].ch[0]].d]; }
int merge(int x, int y)
{
if (!x || !y)
return x | y;
if (t[x].val < t[y].val)
swap(x, y);
rs(x) = merge(rs(x), y);
t[x].d = t[rs(x)].d + 1;
return x;
}
左偏树的其它操作
插入节点
单个节点也可以视为一个堆,合并即可。
删除根
合并根的左右儿子即可。
删除任意节点
做法
先将左右儿子合并,然后自底向上更新 d i s t \mathrm{dist} dist、不满足左偏性质时交换左右儿子,当 d i s t \mathrm{dist} dist 无需更新时结束递归:
int &rs(int x) { return t[x].ch[t[t[x].ch[1]].d < t[t[x].ch[0]].d]; }
// 有了 pushup,直接 merge 左右儿子就实现了删除节点并保持左偏性质
int merge(int x, int y)
{
if (!x || !y)
return x | y;
if (t[x].val < t[y].val)
swap(x, y);
t[rs(x) = merge(rs(x), y)].fa = x;
pushup(x);
return x;
}
void pushup(int x)
{
if (!x)
return;
if (t[x].d != t[rs(x)].d + 1)
{
t[x].d = t[rs(x)].d + 1;
pushup(t[x].fa);
}
}
复杂度分析
我们令当前 pushup 的这个节点为
x
x
x,其父亲为
y
y
y,一个节点的「初始
d
i
s
t
\mathrm{dist}
dist」为它在 pushup 前的
d
i
s
t
\mathrm{dist}
dist。我们先 pushup 一下删除的节点,然后从其父亲开始起讨论复杂度。
继续递归下去有两种情况:
- x x x 是 y y y 的右儿子,此时 y y y 的初始 d i s t \mathrm{dist} dist 为 x x x 的初始 d i s t \mathrm{dist} dist 加一。
- x x x 是 y y y 的左儿子,只有 y y y 的左右儿子初始 d i s t \mathrm{dist} dist 相等时(此时左儿子 d i s t \mathrm{dist} dist 减一会导致左右儿子互换)才会继续递归下去,因此 y y y 的初始 d i s t \mathrm{dist} dist 仍然是 x x x 的初始 d i s t \mathrm{dist} dist 加一。
所以,我们得到,除了第一次 pushup(因为被删除节点的父亲的初始
d
i
s
t
\mathrm{dist}
dist 不一定等于被删除节点左右儿子合并后的初始
d
i
s
t
\mathrm{dist}
dist 加一),每递归一层
x
x
x 的初始
d
i
s
t
\mathrm{dist}
dist 就会加一,因此最多递归
O
(
log
n
)
O(\log n)
O(logn) 层。
整个堆加上/减去一个值、乘上一个正数
其实可以打标记且不改变相对大小的操作都可以。
在根打上标记,删除根/合并堆(访问儿子)时下传标记即可:
int merge(int x, int y)
{
if (!x || !y)
return x | y;
if (t[x].val > t[y].val)
swap(x, y);
pushdown(x);
t[x].rs = merge(t[x].rs, y);
if (t[t[x].rs].d > t[t[x].ls].d)
swap(t[x].ls, t[x].rs);
t[x].d = t[t[x].rs].d + 1;
return x;
}
int pop(int x)
{
pushdown(x);
return merge(t[x].ls, t[x].rs);
}
随机合并
直接贴上代码。
int merge(int x, int y)
{
if (!x || !y)
return x | y;
if (t[y].val < t[x].val)
swap(x, y);
if (rand() & 1) // 随机选择是否交换左右子节点
swap(t[x].ls, t[x].rs);
t[x].ls = merge(t[x].ls, y);
return x;
}
可以看到该实现方法唯一不同之处便是采用了随机数来实现合并,这样一来便可以省去 d i s t \mathrm{dist} dist 的相关计算。且平均时间复杂度亦为 O ( log n ) O(\log n) O(logn),详细证明可参考 Randomized Heap。
The pairing heap: a new form of self-adjusting heap ↩︎ ↩︎
On the efficiency of pairing heaps and related data structures ↩︎
Improved upper bounds for pairing heaps ↩︎
Towards a Final Analysis of Pairing Heaps ↩︎