今日份题目：

给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数。

题目数据保证答案符合 32 位带符号整数范围。

示例1

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit选前两个b
rabbbit选后两个b
rabbbit选两头的b

示例2

输入：s = "babgbag", t = "bag"
输出：5

提示

1 <= s.length, t.length <= 1000
s 和 t 由英文字母组成

题目思路

这道题目的思路和之前的子序列的思路不太一样的地方在于，这道题用到的是当前位置到字符串最后位置的子问题，而之前的题是当前位置到开头位置的子问题。

状态转移方程：

当 s[i]=t[j] 时，dp [ i ] [ j ]由两部分组成：

如果 s[i]和 t[j]匹配，则考虑 t[j+1:] 作为 s[i+1:]的子序列，子序列数为 dp [ i+1 ] [ j+1 ]；

如果 s[i] 不和 t[j] 匹配，则考虑 t[j:] 作为 s[i+1:]的子序列，子序列数为 dp [ i+1 ] [ j ]。

因此当 s[i]=t[j] 时，有 dp [ i ] [ j ] =dp [ i+1 ] [ j+1 ]+dp[ i+1 ] [ j ]。

当 s[i]≠t[j] 时，s[i]不能和 t[j]匹配，因此只考虑 t[j:]作为 s[i+1:] 的子序列，子序列数为 dp[i+1] [j]。

因此当 s[i]≠t[j] 时，有 dp [ i ] [ j ]=dp [ i+1 ] [ j ]。

得状态转移总方程：

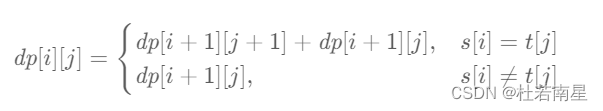
这道题目好难，我也是有点晕，如果大家有疑问，欢迎评论区讨论哦！

代码

class Solution 
{
public:
    int numDistinct(string s, string t) 
    {
        //获取两个字符串的长度
        int n= s.length();
        int m= t.length();
        if (n<m) return 0;

        unsigned long long dp[2000][2000]={0};

        //初始化边界数值
        for(int i=0;i<=n;i++)//此时t[m->末尾]为空字符串，故对于任何字符串，空字符串都是其子序列，为1 
        {
            dp[i][m]=1;
        }

        //更新所有dp值
        for(int i=n-1;i>=0;i--) 
        {
            char sc=s[i];
            for(int j=m-1;j>=0;j--) 
            {
                char tc=t[j];
                if(sc==tc) 
                {
                    dp[i][j]=dp[i+1][j+1]+dp[i+1][j];
                } 
                else 
                {
                    dp[i][j]=dp[i+1][j];
                }
            }
        }
        return dp[0][0];
    }
};