迪锐克斯拉算法
简单来说就是在有向图中，给定一个图中具体的出发点，从这个点出发能够到达的所有的点，每个点的最短距离是多少。到不了的点，距离则是正无穷。有向，无负权重，可以有环。
所以说，迪锐克斯拉算法是生成一个从源点出发到各个点的最小距离表。
举例：有向图如图所示

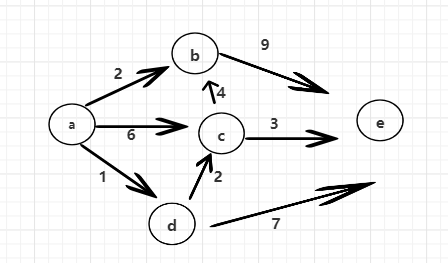
从给定的出发点a出发，最终要获得的是a到b,c,d,e每个点之间的最短距离。默认a到自己的距离是0，其他的点还没到达的点的距离是正无穷。已经确定的答案不动，在没有确定的记录中找一个最小的出来。

a	b	c	d	e
0	正无穷	正无穷	正无穷	正无穷

所以先从a点出发的三条边1，2，6。中找出权重为1的边，ad距离为1，小于之前的正无穷（比之前距离小），所以更新a到d之间的距离，bcd同理。所以更新完后距离如下：

a	b	c	d	e
0	2	6	1	正无穷

此时，从a出发的三条边已经走完，所以a点确定下来，再也不动。
其余没有确定的记录中d是最短的（从a出发到b的距离为1），所以从d开始向下找（d属于中间的跳点）。
d出发的边有两条，分别是dc和de。其中dc距离为2，再加上之前a到d的距离为1，所以此时a到c的距离经过d跳转后为3，小于之前的6，所以更新ac之间距离，同样de距离7小于正无穷。所以也进行更新。d也确定了。

a	b	c	d	e
0	2	3	1	7

接下来从不确定的记录中根据最小的向下找。b点出发的边有一条be，be距离9加上a到b的距离2，所以be距离为11，大于之前的，不更新。b也确定了。

a	b	c	d	e
0	2	3	1	7

还剩下c，从c点出发的边有两条，cb和ce，因为b点已经确定了不再动，所以一看ce一条，ce距离为3，a到c距离为3，所以ae之间距离为6，小于之前，更新e点距离。

a	b	c	d	e
0	2	3	1	6

代码
根据上面的分析进行代码的实现，不过getMinDistanceAndUnSelectNode有瑕疵，因为每找一个minNode就会在集合中都遍历一次。会在下面进行代码优化。

  public static HashMap<Node, Integer> dijkstra1(Node from) {

        HashMap<Node, Integer> distanceMap = new HashMap<>();
        distanceMap.put(from, 0);
        //已经确定的边；
        HashSet<Node> selectedNodes = new HashSet<>();
        //根据已经确定的记录 和 map，找出没确定的中最小的记录
        Node minNode = getMinDistanceAndUnSelectNode(distanceMap, selectedNodes);

        while (minNode != null) {
            int distance = distanceMap.get(minNode);

            for (Edge edge : minNode.edges) {
                Node toNode = edge.to;
                if (!distanceMap.containsKey(toNode)) {
                    distanceMap.put(toNode, distance + edge.weight);
                } else {
                    //edge.weight + distance 当前边的权重 + 我此时当做跳点的距离。
                    //distanceMap.get(toNode) 已经存在的距离
                    distanceMap.put(toNode, Math.min(distanceMap.get(toNode), (edge.weight + distance)));
                }
            }
            //所有的边都已经遍历完，这个点可以确定了，放到确定的集合中。
            selectedNodes.add(minNode);
            //再次获取最小的记录
            minNode = getMinDistanceAndUnSelectNode(distanceMap, selectedNodes);
        }
        return distanceMap;
    }

    public static Node getMinDistanceAndUnSelectNode(HashMap<Node, Integer> distanceMap, HashSet<Node> selectedNode) {
        Node minNode = null;
        int minDistance = Integer.MAX_VALUE;
        
        for (Map.Entry<Node, Integer> entry : distanceMap.entrySet()) {
            Node node = entry.getKey();
            int distance = entry.getValue();

            if (!selectedNode.contains(node) && distance < minDistance) {
                minDistance = distance;
                minNode = node;
            }
        }
        return minNode;
    }