文章目录
- 模型特点
- 使用技巧
- 工具包和求解器
- 模型线性化
- 应用实例
- 经验总结
模型特点
上一篇中,详细阐述了线性规划问题和单纯形法的算法原理,本文将着重介绍线性模型在工业场景中的应用。
首先需要说清楚的是,为什么线性模型深受研发人员青睐。
从已有的经验来看,主要原因有三个:(1)线性规划的局部最优解就是全局最优解;(2)计算速度快;(3)研发成本低。
为了说明第一点,需要先引入一个概念:凸函数。
凸函数的定义为:设函数
f
f
f的定义域是凸集,且对于
θ
∈
[
0
,
1
]
\theta\in[0,1]
θ∈[0,1],
f
f
f上任意两点
x
x
x和
y
y
y均满足
f
(
θ
x
+
(
1
−
θ
)
y
)
≤
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
f(\theta x + (1-\theta)y) ≤ \theta f(x) + (1-\theta)f(y)
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
则称函数
f
f
f为凸函数。下图是一个凸函数的示意图,显然用直线连接函数上的任意两点A和B,线段AB上的点都在函数的上方。

在线性规划问题中,目标函数为线性加和的表达式,显然也是凸函数。
有了这个概念后,我们做以下推演:
假设 x ⋆ x^\star x⋆是线性规划问题的一个局部最优解,即在 x ⋆ x^\star x⋆附近存在一个邻域,在该邻域内所有的点都比 f ( x ⋆ ) f(x^\star) f(x⋆)大。
此时构造一个新的
x
=
(
1
−
t
)
x
⋆
+
t
y
x=(1-t)x^\star + ty
x=(1−t)x⋆+ty,只要
t
t
t足够小,那么
x
x
x就能出现在
x
⋆
x^\star
x⋆的邻域内,即
f
(
x
⋆
)
≤
f
(
(
1
−
t
)
x
⋆
+
t
y
)
f(x^\star)≤f((1-t)x^\star + ty)
f(x⋆)≤f((1−t)x⋆+ty)
由于
f
f
f是凸函数,所以必然满足
f
(
(
1
−
t
)
x
⋆
+
t
y
)
≤
(
1
−
t
)
f
(
x
⋆
)
+
t
f
(
y
)
f((1-t) x^\star + ty) ≤(1-t) f(x^\star) + tf(y)
f((1−t)x⋆+ty)≤(1−t)f(x⋆)+tf(y)
上面两式结合一下,同时消去
f
(
x
⋆
)
f(x^\star)
f(x⋆),可以得到
f
(
x
⋆
)
≤
f
(
y
)
f(x^\star)≤f(y)
f(x⋆)≤f(y)
由于
y
y
y是任意的,所以
x
⋆
x^\star
x⋆是全局最优解。
这就意味着,不管使用哪个策略,只要找到了一个局部最优解,那就肯定也是全局最优解。
针对计算速度快的说明,有些复杂,这里直接给出结论:针对线性规划问题,使用单纯形法求解,最差情况下是指数级复杂度,但平均复杂度是多项式时间;如果使用内点法求解,是多项式复杂度。
至于研发成本,在下一节中将会看到,在商用/开源求解器的加持下,主要研发成本只剩下问题建模和模型代码化。
使用技巧
得益于上述特点,研发人员会遇到优化问题时,会想方设法地使用线性模型。那么具体到任意一个场景,该如何使用线性模型呢?
工具包和求解器
此前我们已经提过,单纯形法是求解线性规划问题的高效算法,但是在实际应用时,我们并不需要像运筹学教材里描述的那样,去手撕单纯形表。这主要是因为,目前已经有非常多的求解器可以辅助我们做模型的优化计算。文章中列举了很多求解器,这里做个简单汇总。
| 商用求解器 | 开源求解器 | 其他软件集成 |
|---|---|---|
| Gurobi,Cplex,Xpress,Mosek, BARON, Lingo, COPT, MindOPT, OPTV | SCIP,Coin-OR套件CLP/CBC/CGL/SYMPHONY,LP_solve, GLPK,OR-Tools,CMIP, Leaves | MATLAB,SAS,SCIPy,Excel |
总体上来说,商业求解器的求解能力是最强的,主要体现在可解决的问题类型多和计算速度快两个方面;开源求解器的求解能力次之,不过根据我个人的经验,针对0-1规划问题,当优化变量是百万量级时,求解时间差不多是小时量级,所以针对大部分的实际问题,应该是够用的;其他软件集成的求解器基本只能应付小规模的问题,使用率很低。
在排除违规使用学术版商业求解器的情况下,工业场景里用的比较多的是OR-Tools,个人理解应该是大家普遍信赖Google这个品牌。
模型线性化
既然算法实现已经有现成的求解器了,那需要我们做的,其实就只剩两件事了:(1)建立线性规划模型;(2)模型代码化。
本节只说第一个,第二个在下一节中通过一个实例来描述。
回顾一下线性规划的标准型
m
i
n
f
(
x
)
=
c
T
x
s.t
A
x
=
b
x
≥
0
min \quad f(\pmb x)=\pmb c^T\pmb x \\ \text{s.t} \quad A\pmb x=\pmb b \\ \quad \quad \pmb x ≥ 0
minf(x)=cTxs.tAx=bx≥0
其实,这个模型的限制还是挺多的。大部分问题被直接建模后,可能都不满足这些条件。
最普遍的不满足标准型的情况有三种:(1) 约束为不等式;(2)优化目标是最大化表达式;(3)优化变量的范围中包含负数。如果是这些情况,目前的大多数求解器是支持直接输入的,即无需将其变为标准型也不影响正常求解。
如果再复杂一点,就需要对原有的模型做一些额外改造,使其满足线性规划的要求,即模型线性化。得益于大佬们的分享,线性化的方法也已经被提前整理好了,详见文章。这里我也做个简单汇总。
| 编号 | 非线性表达式 |
|---|---|
| 1 | 分段函数 |
| 2 | 绝对值函数 |
| 3 | MaxMin/MinMax函数 |
| 4 | 逻辑或 |
| 5 | MinMin/MinMin函数 |
| 6 | 含有0-1变量的乘积形式 |
| 7 | 分式表达式 |
| 8 | max/min函数 |
| 9 | 混合整数 |
也就是说,如果我们的原始模型是以上表中的表达式,那就可以通过一些改造使其变为线性模型。
不过这里还有个偷懒的小技巧,就是有些求解器的功能已经非常强大,允许我们直接输入部分种类的非线性表达式,比如Gurobi就可以直接添加绝对值函数和max函数等。所以如果确定了要使用某个求解器后,可以先了解清楚其支持的表达式种类,再看应该把模型细致到哪个程度。
应用实例
本节以一个线性规划问题为例,详细描述如何使用python调用ortools求解器,顺便给上一节模型线性化的事情填坑。
事实上,ortools的官网上已经有些例子了,但是在刚开始使用时,还是会有一些小问题:问题规模较大时怎么操作;如何判断所建立的模型是否正确等。
为了解答上述疑问,接下来以一个实例来说明。
规模大一些后,手动输入目标函数和约束条件中的系数是不现实的,一般我会提前将这些系数存到一个dataframe中,比如下图中的 A , B , C \pmb A, \pmb B, \pmb C A,B,C。
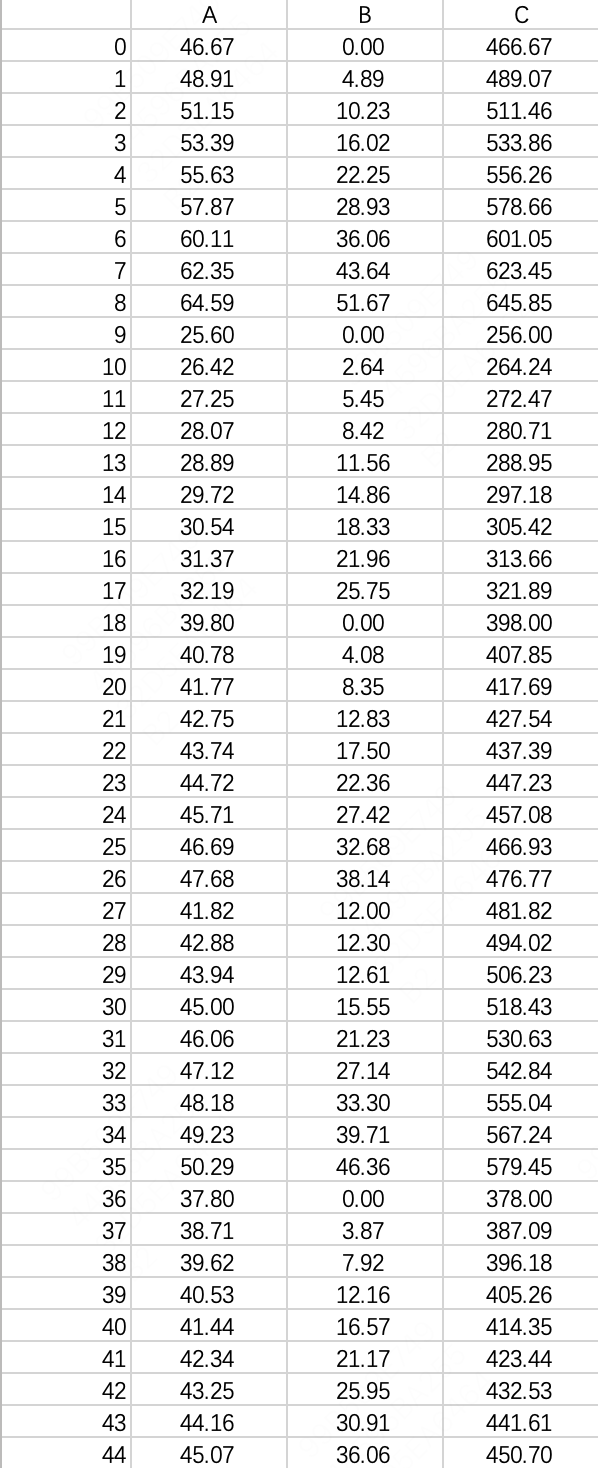
线性模型可以描述为:
(1) 优化变量
x
\pmb x
x为
0
≤
x
i
≤
1
,
i
=
0
,
.
.
.
,
44
0≤x_i≤1,i=0,...,44
0≤xi≤1,i=0,...,44
(2) 目标函数为
m
a
x
[
A
−
0.5
B
]
T
x
max \quad [\pmb A-0.5\pmb B]^T\pmb x
max[A−0.5B]Tx
(3) 约束条件有两组,第一组是
∑
i
=
0
8
x
9
j
+
i
=
1
,
j
=
0
,
1
,
.
.
,
4
\sum_{i=0}^8x_{9j+i}=1, \quad j=0,1,..,4
i=0∑8x9j+i=1,j=0,1,..,4
第二组是
[
B
−
0.05
C
]
T
x
≥
0
[\pmb B-0.05\pmb C]^T\pmb x ≥ 0
[B−0.05C]Tx≥0
算法实现的全流程包括:声明求解器->定义优化变量、目标函数和约束条件->模型求解->打印模型->输出最优解。我此前用过ortools、pulp和cplex,流程基本是通用的,主要的区别在于具体表达的方式。
ortools的实现代码如下
import pandas as pd
from ortools.linear_solver import pywraplp
import time
if __name__ == '__main__':
coef_df = pd.read_csv('lp_data.csv')
# 统计模型计算时间时使用
time0 = time.time()
# 声明ortools求解器,使用SCIP算法
solver = pywraplp.Solver.CreateSolver('SCIP')
# 优化变量
x = {}
for j in range(len(coef_df)):
x[j] = solver.NumVar(0, 1, 'x[%i]' % j)
# 目标函数
obj_expr = [(coef_df['A'].iloc[j] - 0.5 * coef_df['B'].iloc[j]) * x[j] for j in range(len(coef_df))]
solver.Maximize(solver.Sum(obj_expr))
# 约束条件一
for i in range(int(len(coef_df) / 9)):
constraint_expr = [x[i * 9 + j] for j in range(9)]
solver.Add(sum(constraint_expr) == 1)
# 约束条件二
constraint_expr = [(coef_df['B'].iloc[j] - 0.05 * coef_df['C'].iloc[j]) * x[j] for j in
range(len(coef_df))]
solver.Add(solver.Sum(constraint_expr) >= 0)
# 模型求解
status = solver.Solve()
# 打印模型
fw = open('ortools output model.lp', 'w', encoding='utf-8')
fw.write(solver.ExportModelAsLpFormat(True))
fw.write("\n")
# 模型求解成功, 打印结果
if status == pywraplp.Solver.OPTIMAL:
# 变量最优解
print('best_x = [')
for j in range(len(coef_df)):
print('{:.2f}'.format(x[j].solution_value()), end=" ")
if (j+1) % 9 == 0 and j+1 < len(coef_df):
print()
print(']')
# 最优目标函数值
print('best_f =', solver.Objective().Value())
# 约束条件值
cons_2 = 0
for j in range(len(coef_df)):
cons_2 += x[j].solution_value() * (coef_df['B'].iloc[j] - 0.05 * coef_df['C'].iloc[j])
print('cons_2 = {:.2f}'.format(cons_2))
else:
print('not converge.')
print('cost time: {}'.format(time.time() - time0))
运行代码后,可以得到优化解如下。
best_x = [
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 1.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 1.00
0.00 0.00 0.00 1.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 1.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.53 0.47 0.00 0.00 0.00 0.00 0.00 ]
best_f = 166.72005627038578
cons_2 = 0.00
cost time: 0.08336210250854492
然后在代码所在文件夹中可以找到一个ortools output model.lp文件,打开后内容如下。这里详细展示了我们的模型内容,可以用来校验代码是否都已经编写正确。
\ Generated by MPModelProtoExporter
\ Name :
\ Format : Free
\ Constraints : 6
\ Variables : 45
\ Binary : 0
\ Integer : 0
\ Continuous : 45
Maximize
Obj: +46.67 V00 +46.4646 V01 +46.0351 V02 +45.3817 V03 +44.5044 V04 +43.403 V05 +42.0777 V06 +40.5284 V07 +38.7551 V08 +25.6 V09 +25.1025 V10 +24.5226 V11 +23.8604 V12 +23.1158 V13 +22.2888 V14 +21.3795 V15 +20.3878 V16 +19.3137 V17 +39.8 V18 +38.7454 V19 +37.5924 V20 +36.3409 V21 +34.9909 V22 +33.5425 V23 +31.9956 V24 +30.3502 V25 +28.6064 V26 +35.82 V27 +36.7272 V28 +37.6345 V29 +37.2212 V30 +35.4442 V31 +33.5451 V32 +31.5241 V33 +29.381 V34 +27.1158 V35 +37.8 V36 +36.7733 V37 +35.6558 V38 +34.4474 V39 +33.148 V40 +31.7579 V41 +30.2768 V42 +28.7049 V43 +27.0421 V44
Subject to
C0: +1 V00 +1 V01 +1 V02 +1 V03 +1 V04 +1 V05 +1 V06 +1 V07 +1 V08 = 1
C1: +1 V09 +1 V10 +1 V11 +1 V12 +1 V13 +1 V14 +1 V15 +1 V16 +1 V17 = 1
C2: +1 V18 +1 V19 +1 V20 +1 V21 +1 V22 +1 V23 +1 V24 +1 V25 +1 V26 = 1
C3: +1 V27 +1 V28 +1 V29 +1 V30 +1 V31 +1 V32 +1 V33 +1 V34 +1 V35 = 1
C4: +1 V36 +1 V37 +1 V38 +1 V39 +1 V40 +1 V41 +1 V42 +1 V43 +1 V44 = 1
C5: -23.3335 V00 -19.5627 V01 -15.3439 V02 -10.6772 V03 -5.5626 V04 -3.55271e-15 V05 +6.01055 V06 +12.469 V07 +19.3755 V08 -12.8 V09 -10.5695 V10 -8.17421 V11 -5.61421 V12 -2.88947 V13 +3.05421 V15 +6.27315 V16 +9.65684 V17 -19.9 V18 -16.3139 V19 -12.5308 V20 -8.5508 V21 -4.37387 V22 +4.5708 V24 +9.33853 V25 +14.3032 V26 -12.091 V27 -12.3972 V28 -12.7035 V29 -10.3686 V30 -5.30634 V31 +5.55041 V33 +11.3449 V34 +17.3834 V35 -18.9 V36 -15.4835 V37 -11.8853 V38 -8.10526 V39 -4.14351 V40 +4.32526 V42 +8.83227 V43 +13.521 V44 >= 0
Bounds
0 <= V00 <= 1
0 <= V01 <= 1
0 <= V02 <= 1
0 <= V03 <= 1
0 <= V04 <= 1
0 <= V05 <= 1
0 <= V06 <= 1
0 <= V07 <= 1
0 <= V08 <= 1
0 <= V09 <= 1
0 <= V10 <= 1
0 <= V11 <= 1
0 <= V12 <= 1
0 <= V13 <= 1
0 <= V14 <= 1
0 <= V15 <= 1
0 <= V16 <= 1
0 <= V17 <= 1
0 <= V18 <= 1
0 <= V19 <= 1
0 <= V20 <= 1
0 <= V21 <= 1
0 <= V22 <= 1
0 <= V23 <= 1
0 <= V24 <= 1
0 <= V25 <= 1
0 <= V26 <= 1
0 <= V27 <= 1
0 <= V28 <= 1
0 <= V29 <= 1
0 <= V30 <= 1
0 <= V31 <= 1
0 <= V32 <= 1
0 <= V33 <= 1
0 <= V34 <= 1
0 <= V35 <= 1
0 <= V36 <= 1
0 <= V37 <= 1
0 <= V38 <= 1
0 <= V39 <= 1
0 <= V40 <= 1
0 <= V41 <= 1
0 <= V42 <= 1
0 <= V43 <= 1
0 <= V44 <= 1
End
经验总结
作为一个工作了近3年的运筹优化算法工程师,对线性模型的工程应用算是比较熟悉的了。本节以场景对计算实时性的高低来做区分,分别描述个人的认知和经验。
对于那些实时性要求不高、更追求最优性的场景,比如路径规划、生产排程、排班定编等场景,只需每天、每周、甚至每月调度一次,可以考虑直接使用线性模型。
不过为了保证线上流程的稳定性,这类算法在设计时一般都需要额外增加一个兜底的启发式算法,这样的话,即使线性模型在特殊情况下无法在给定时间内输出最优解,也可以让启发式解决算法及时透出一个可行解。
对于那些实时性要求高的场景,比如骑手派单算法,一般更适合使用启发式算法。但即使是在这种情况下,线性模型依然具有重要价值:离线评估启发式算法的最优性,定量给出已有算法解和最优解之间的gap。gap的表达形式可能是这样的:变量数小于等于10时,针对随机生成/历史上的100个问题实例,启发式算法100%可以找到最优解,计算耗时和线性模型相当;当变量数增长至30时,启发式算法可以找到80%的最优解,计算耗时约为线性模型的10%,未找到最优解的问题中,gap的均值10%;当变量数增长至50时,启发式算法可以找到30%的最优解,计算耗时约为线性模型的1%,未找到最优解的问题中,gap约50%。
对于前者,模型研发完后几乎就没有多少改进空间,虽然可能还有相关的事情要做,比如模型的部分输入内容包含预测数据,存在数据不准确现象;落地过程中遭遇业务阻力,推广不那么顺利等,但是这些问题的解决,都不再是算法方面的进展,所以本质上是很费场景的,也就是说,要想持续有算法进展,可能就需要研发人员频繁寻找新场景。
但是对于后者,由于可以在优化gap的方向持续做功,比如提升计算速度、降低与最优解之间的gap等,所以相对来说,算法方面可以做的事情就稍微多一些。不过,需要谨防的陷阱是,只关注gap值的自身变化,而忽略了gap对业务的影响。一般情况下,gap减少的难度是递增的,对业务的影响却是递减的,所以当gap减少到一定程度,可能就没有再继续优化的必要了,是否已经达到临界点需要时刻思考。





![[鹏城杯 2022]简单包含](https://img-blog.csdnimg.cn/0ff96b875af747b0b2d3aa2b16208c82.png)






![[FPGA IP系列] 2分钟了解FPGA中的BRAM](https://img-blog.csdnimg.cn/b4c99a625a2c4f84a061586a235d883d.png)
