个人对哈希数据结构学习总结 -- 理论篇

引言
哈希表设计思考
- 哈希冲突
- - Hash Functions
  - 冲突解决
  - - 开放地址法(Open Addressing)
    - 分离链表法(Separate Chaining)
    - Two-way Chaining
  - Dynamic Hash Tables
  - - chained Hashing
    - extendible hashing
    - linear hashing
    - - 说明
    - spiral storage
使用场景
小结

引言

哈希表这个数据结构相信各位都不陌生，无论是高级语言，还是各大数据库底层实现都不离开它，所以本文我想来聊聊我个人对哈希表的一些看法，同时也是对哈希表这个知识点做一次系统性的梳理和总结。

本文主要会分为两大部分:

哈希表设计思考(偏理论)
最佳实践(结合Java,Go,redis等热门技术来谈谈其中使用到的哈希设计原则)

哈希表设计思考

对于哈希表这个数据结构而言，有这样四个维度的指标是我们需要考虑的:

所有数据集合 S
哈希表存储的数据集合 U
所有哈希桶的下标集合 R
映射函数 h

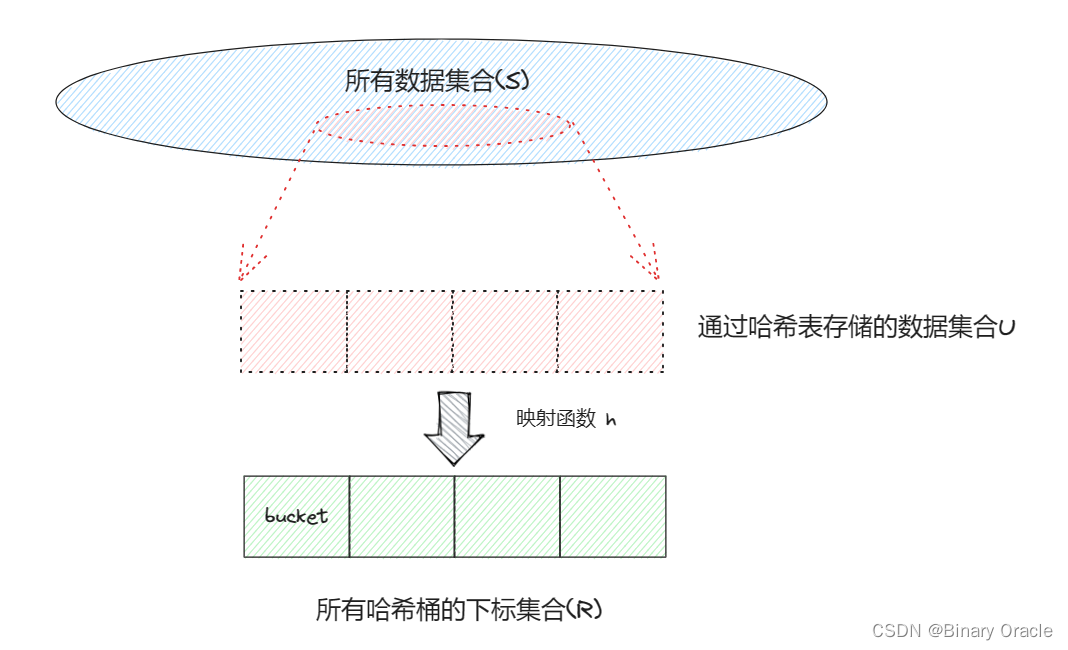
S的大小一般远大于R，但是哈希表存储的数据集合 U 与 R 大小相差不会太大；如果存在 x!=y && h(x) == h(y) ,则称x与y冲突。

如果h可以将U单射到R上，那么我们称这种情况为完美哈希(perfect hashing) , 并且如果此时U的大小与R的大小相等，则称此种情况为最小完美哈希(minimal perfect hashing)。

如果U的大小是固定的并且预先可知，那么称这种情况为静态哈希表，否则称之为动态哈希表。

哈希冲突

解决哈希冲突有两个着眼点：

在冲突没发生前尽量避免冲突，在冲突发生后解决冲突

Hash Functions

要避免冲突，我们需要从哈希函数h这个维度下手：

对于静态哈希表，我们总是可以找到一个h来达成最小完美哈希
对于动态哈希表，由于集合U是不可控的，所以我们的思路是尽可能减少冲突发生，也就是选择一个尽可能少冲突的哈希函数h

关于如何设计一个完美的哈希函数并不是本文重点，但是比较出名的哈希函数有以下这些，大家可以自行查阅资料了解各自适用场景:

MurmurHash (2008)
Google CityHash (2011)
Google FarmHash (2014)
CLHash (2016)

冲突解决

动态哈希表很难达成完美哈希的情况，因此我们必须考虑如何解决发生的哈希冲突，常见的冲突解决策略有:

开放地址法(Open Addressing)
分离链表法(Separate Chaining)
Two-way Chaining

开放地址法(Open Addressing)

开放地址法(Open Addressing)下面又细分了好几种策略:

线性探测法（Linear Probing）：发生哈希冲突时，将会在哈希表中线性地往后查找，直到找到一个空槽来插入元素或执行查找操作。
- 这种方法可能导致聚集（clustering）现象，即冲突的元素会聚集在一起，影响性能。
二次探测法（Quadratic Probing）：发生冲突时，会使用二次函数来计算下一个探测位置，以尝试寻找下一个空槽或者目标元素。
- 这种方法相对于线性探测法来说，能够更均匀地分散元素，但仍然可能会出现二次探测路径相交的情况。
双重散列（Double Hashing）：双重散列使用两个哈希函数，当发生冲突时，首先使用第一个哈希函数得到一个偏移量，然后在第二个哈希函数的值处查找下一个位置。
- 这个方法可以有效地减少聚集问题，但需要选择合适的哈希函数和冲突解决策略。

其中 Linear probing 由于对缓存友好，性能最高，比较常用。Linear probing 可能带来冲突聚集的情况，为了避免这一现象，有时也会使用 Quadratic probing 策略。使用 Quadratic probing 也会遇到一些恶意操作或者特定的输入数据，从而导致性能下降或其他问题，因此有时也会使用 Double hashing 配合 Universal hashing 获得更好的效果。

1.“线性探测对缓存友好” 指的是线性探测法在某些情况下能够更好地利用计算机的缓存机制，从而在内存访问方面表现较好。这主要是因为线性探测法在哈希冲突时，会沿着一个连续的内存地址序列进行探测，这有助于提高数据的局部性，从而更好地适应现代计算机的缓存体系结构。

2.通用哈希(Universal hashing)的主要思想是，从一组可能的哈希函数中随机选择一个函数来哈希每个键，这样可以使得不同的键在不同的哈希函数下分布，减少冲突的概率。

Robin Hood Hashing:

Linear Probe Hashing 的变种，为了防止 Linear Probe Hashing 出现连续区域导致频繁的 probe 操作。基本思路是 “劫富济贫”，即每次比较的时候，同时需要比较每个 key 距离其原本位置的距离（越近越富余，越远越贫穷），如果遇到一个已经被占用的 slot，如果它比自己富余，则可以直接替代它的位置，然后把它顺延到新的位置。
- Robin Hood Hashing 也是为了解决线性探测法冲突聚集的问题

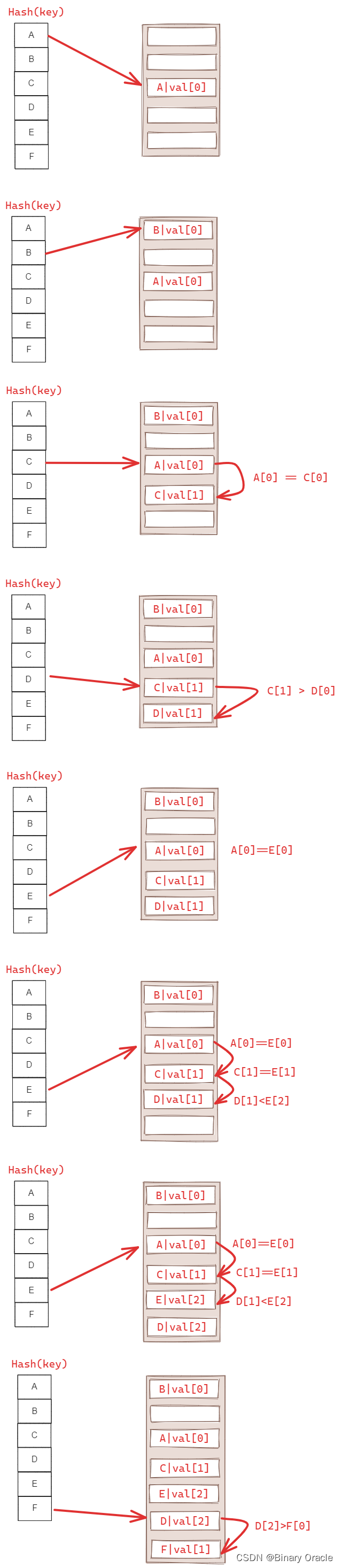
这样做的好处是什么呢？最大的好处就是各个键值对离自己的理想位置的距离变得“均衡”了，或许对查询的平均时间复杂度有一定的优化，但是一定复杂化了插入操作的时间复杂度。

实际上，经过实验发现，这种方法的效率不如线性探测法，不过这种方法的思想还是很有价值的。

分离链表法(Separate Chaining)

开放地址法(Open Addressing) 在装载因子较高时性能会急剧下降，为了应对这一情况，也常使用 Separate Chaining 策略。Separate Chaining 一般使用链表，有时也会使用查找树结构。

Two-way Chaining

Two-way Chaining 就像是 Double hashing，区别在于 Double hashing 使用一个哈希表，而 Two-way Chaining 使用两个哈希表 T1 和 T2。在插入时，T[h1(x)] 和 T[h2(x)] 中哪个装载的元素更少，就插入到哪儿。查找时需要访问两个哈希表。

还有一种和Two-way Chanining思想类似的算法Cuckoo Hashing (布谷鸟哈希) ，要理解该算法，我们首先需要理解布谷鸟的行为，这也是算法的核心:

布谷鸟妈妈从不筑巢，它将自己的鸟蛋生在其他鸟类的巢穴里，要别的鸟给它孵蛋
新出生的布谷鸟会本能地将巢穴里的其他蛋踢开（kick out ），推出鸟巢，以确保自己在鸟巢里可以独享宠爱

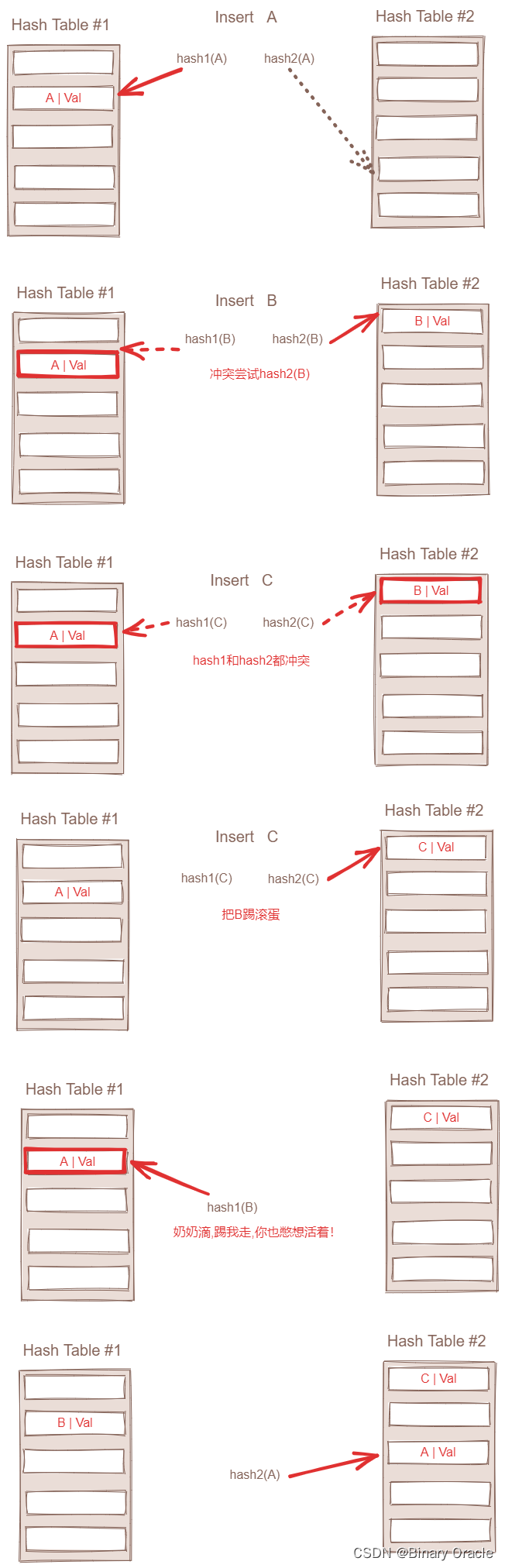
布谷鸟哈希有几种变种，下面介绍一个哈希桶和两个哈希函数的版本：

Insert
1. 若值x已存在哈希表中，则直接返回
2. 若insert后哈希表空间会不够，则先进行扩容，再rehash，再继续3、4、5
3. 用哈希函数h1(x)计算出下标i1，当bucket[i1]为空时，说明鸟巢可用，插入x
4. 若bucket[i1]非空，用新值x将bucket[i1]上的老值x’踢开（kick out），对应小布谷鸟将老蛋踢出巢穴，老蛋当然也不能坐以待毙，继续kick out别的蛋，老值x’的下一个位置用哈希函数h2(x)寻找
5. 重复2，直到达到最大循环次数MaxLoop（插入失败）；或者所有被踢开的值都找到新位置（插入完成）
lookup
- 查找逻辑非常简单，去可能的两个巢穴里寻找，即去下标h1(x)和h2(x)寻找，若没有匹配上，则不存在（从这里可以发现查找是非常快的，且时间复杂度稳定是O(1)）

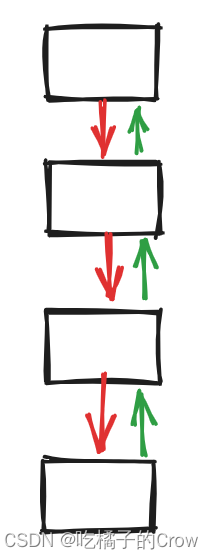
下图展示的是两个哈希函数，两个哈希桶的版本:
在这里插入图片描述

为了防止我们不会陷入一个无限循环中，一旦我们发现了一个死循环或者达到最大循环次数，我们就需要对现有的hash table进行扩容：

如果使用两个hash function，那么我们大概只需要当hash table达到50%容量左右时，才需要进行扩容重建
如果使用三个hash function，那么我们大概需要当hash table达到90%容量的左右时，才需要进行扩容重建

Dynamic Hash Tables

随着哈希表的装载因子上升，哈希冲突的概率会不断上升，直到装载因子超过 1 时，必然发生哈希冲突。对于动态哈希表，由于U 的大小不能预先得知，所以必然需要动态调整哈希表的大小。常见的策略:

当装载因子超过某一阈值后，线性扩展哈希表的大小为原来的若干倍
当装载因子低于某一阈值时，线性收缩哈希表的大小为原来的若干分之一

使用两个阈值的原因是为了避免抖动。

由于R发生变化，对应的哈希函数也必须发生变化，同时分配一个块更大的内存，将原哈希表中所有元素rehash到新的哈希表中，这种策略称为Copy All策略，该策略的坏处就是会产生较长时间的停顿，因此下面来介绍几种改进的策略:

Chained Hashing
extendible hashing
linear hashing
spiral storage

哈希表不能够均匀地增长，其根本原因在于 rehash，只要能够不 rehash 但是调整 R，就可以解决这一问题。

chained Hashing

Chained Hashing 是 Dynamic Hash Tables 的 HelloWorld 实现，每个 key 对应一个链表，每个节点是一个 bucket，装满了就再往后挂一个 bucket。需要写操作时，需要请求 latch:
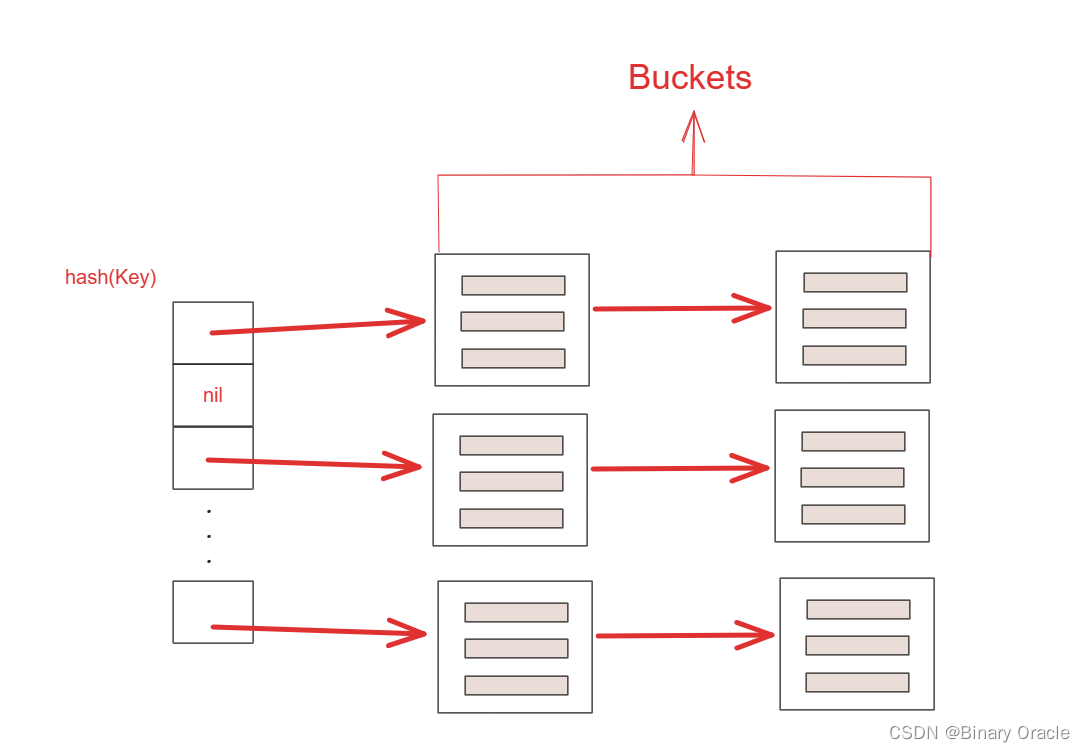
在这里插入图片描述

在查找元素时，根据元素的哈希键计算出对应的槽位，并遍历该槽位的链表桶，搜索具有相同哈希键的元素
对于插入和删除操作，也可以看作是查找操作的一般化。在插入元素时，需要进行查找并确定插入位置；在删除元素时，也需要查找并删除相应元素

这么做的好处就是简单，坏处就是最坏的情况下 Hash Table 可能降级成链表，使得操作的时间复杂度降格为 O(n)。

当然，如果桶中只有一个元素，那么可以将其视为链表，可以在链表长度到达指定阈值后，变成二叉查找树，提升查询效率。并且当负载因子达到指定阈值后，可以对哈希表进行扩容，此时如果不考虑性能，可以采用copy all策略，如果考虑性能，可以考虑渐进式扩容策略。

extendible hashing

在Chained Hashing中，一种可行的方法是在链表变得过长时，将桶（bucket）进行分割，而不是让链表无限增长。这种方法可以避免链表过长导致的性能问题，并且需要进行分割时，只需要对特定的桶进行重新分配。

可扩展哈希方式包含一个slot数组和一系列的buckets，每个slot中保存对应bucket的指针。对于slot数组有一个全局bit位，记录在这个哈希表中需要多少位才能找到对应bucket，对于每一个bucket，有一个本地bit位，记录找到本地的bucket需要多少位。

extendible hash像一种结合hash与redix（前缀树）的技术的哈希方法

Extendible Hashing 的基本思路是一边扩容，一边 rehash，如下图所示：

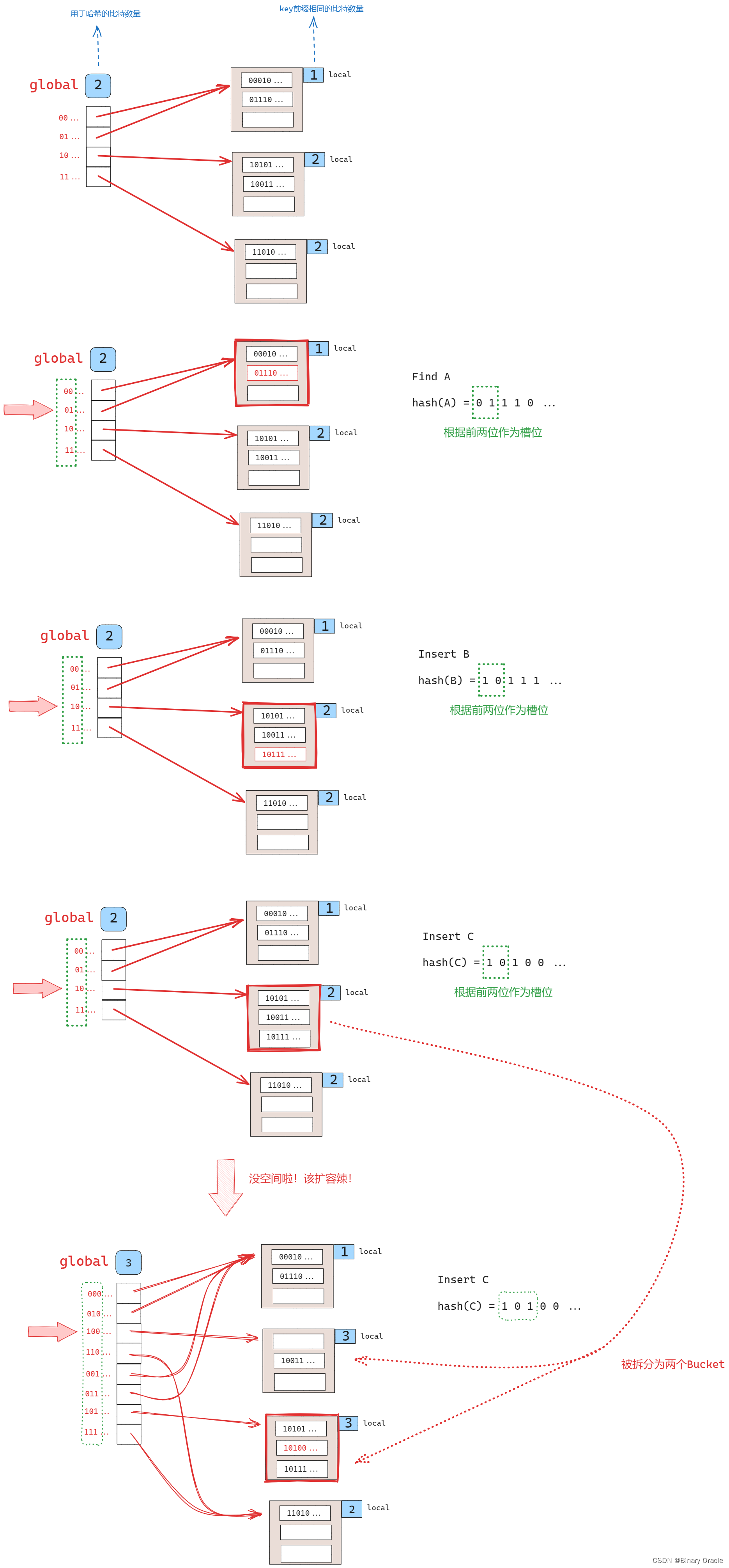
在这里插入图片描述

可拓展哈希允许插入哈希值相同的记录。所以当插入4条哈希值一样的记录，一个桶就一定放不下（假设桶的容纳上限是3条）。这种情况被叫做overflow，而解决方法是用指针指向overflow bucket，也就是人为增加桶。这种方式看上去不美，也暴露了可拓展哈希的局限性，但一个方法在实际应用中确实无法确保永远的统一性，总是会需要“补丁”。实际应用中，可拓展哈希也不是最普遍的方法，更多则是B-Tree。

linear hashing

本部分参考文章

线性哈希是可扩展哈希的改进，可扩展哈希有一个小的性能瓶颈，在bucket分裂且需要扩展slot array时，需要对整个slot array加锁直到bucket分裂完成。为了解决这个问题，提出了线性哈希方式。哈希表维护一个指针，指向下一个准备分裂的bucket，并且线性哈希采用多个哈希函数来寻找正确的bucket。

线性哈希的数学原理:

假定key = 5 、 9 、13

此时所有 key % 4 = 1

现在我们对8求余

由上面的规律可以得出

(任意key) % n = M
(任意key) %2n = M或 (任意key) %2n = M + n

线性哈希的具体实现如所示:

我们假设初始化的哈希表如下:

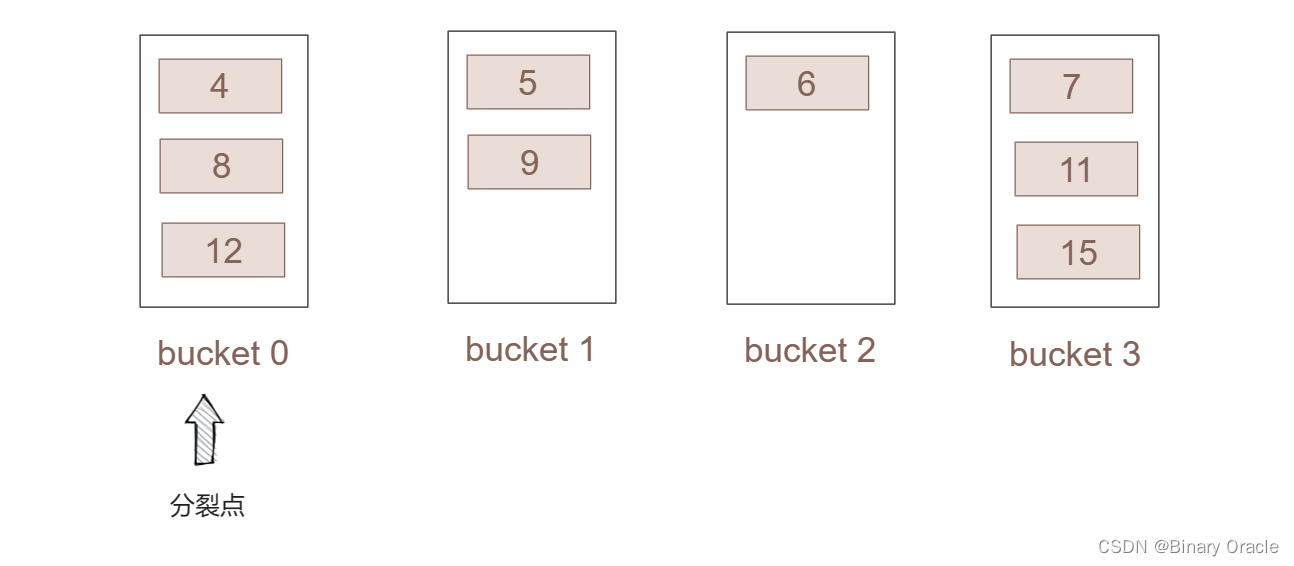
在这里插入图片描述

为了方便叙述，我们作出以下假定:

为了使哈希表能进行动态的分裂，我们从桶0开始设定一个分裂点。
一个桶的容量为listSize = 3，当桶的容量超出后就从分裂点开始进行分裂。
hash函数为 h0 = key %4 h1 = key % 8，h1会在分裂时使用。
整个表初始化包含了4个桶，桶号为0-3，并已提前插入了部分的数据。

分裂过程如下:

现在插入key = 27

进行哈希运算，h0 = 27 % 4 = 3
将key = 27插入桶3，但发现桶3已经达到了桶的容量，所以触发哈希分裂
由于现在分裂点处于0桶，所以我们对0桶进行分割。这里需要注意虽然这里是3桶满了，但我们并不会直接从3桶进行分割，而是从分割点进行分割。这里为什么这么做，在下面会进一步介绍。
对分割点所指向的桶(桶0)所包含的key采用新的hash函数(h1)进行分割。

对所有key进行新哈希函数运算后，将产生如下的哈希表：

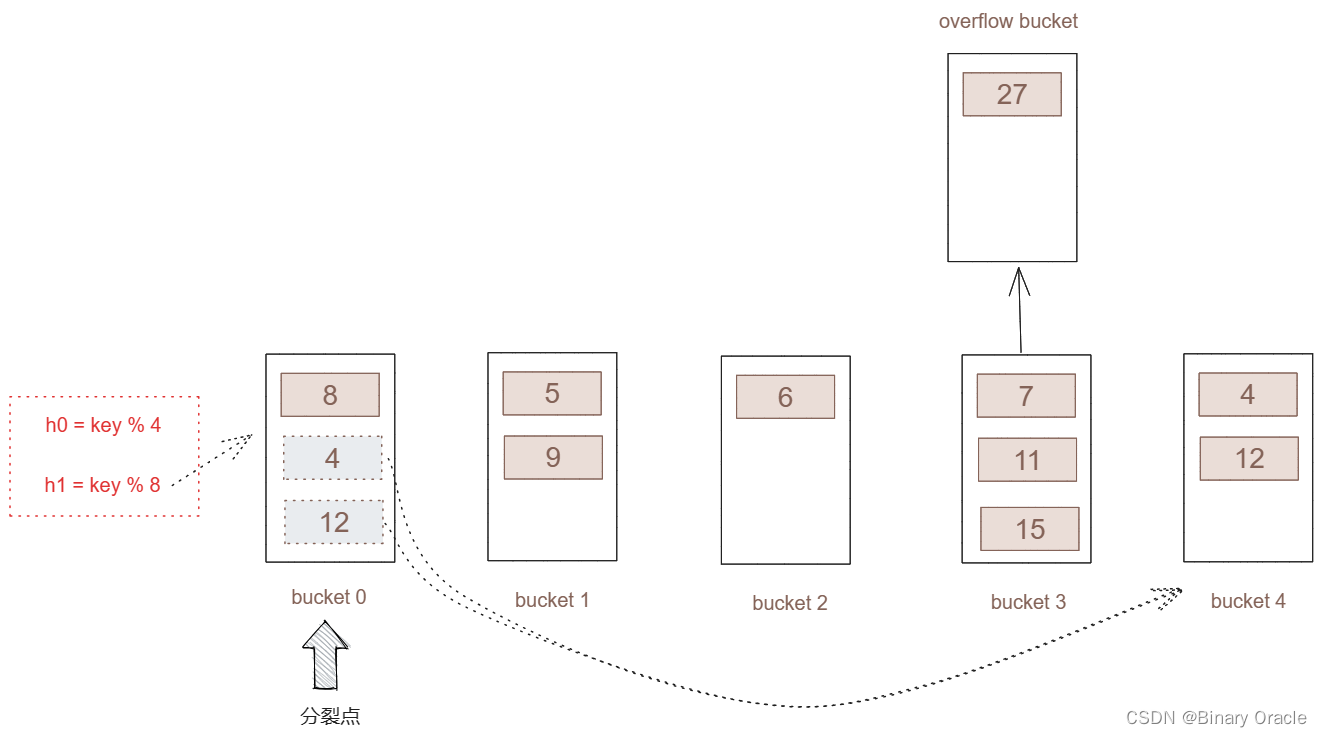
在这里插入图片描述

虽然进行了分裂，但桶3并不是分裂点，所以桶3会将多出的key，放于溢出桶.,一直等到桶3进行分裂。
进行分裂后，将分裂点向后移动一位。

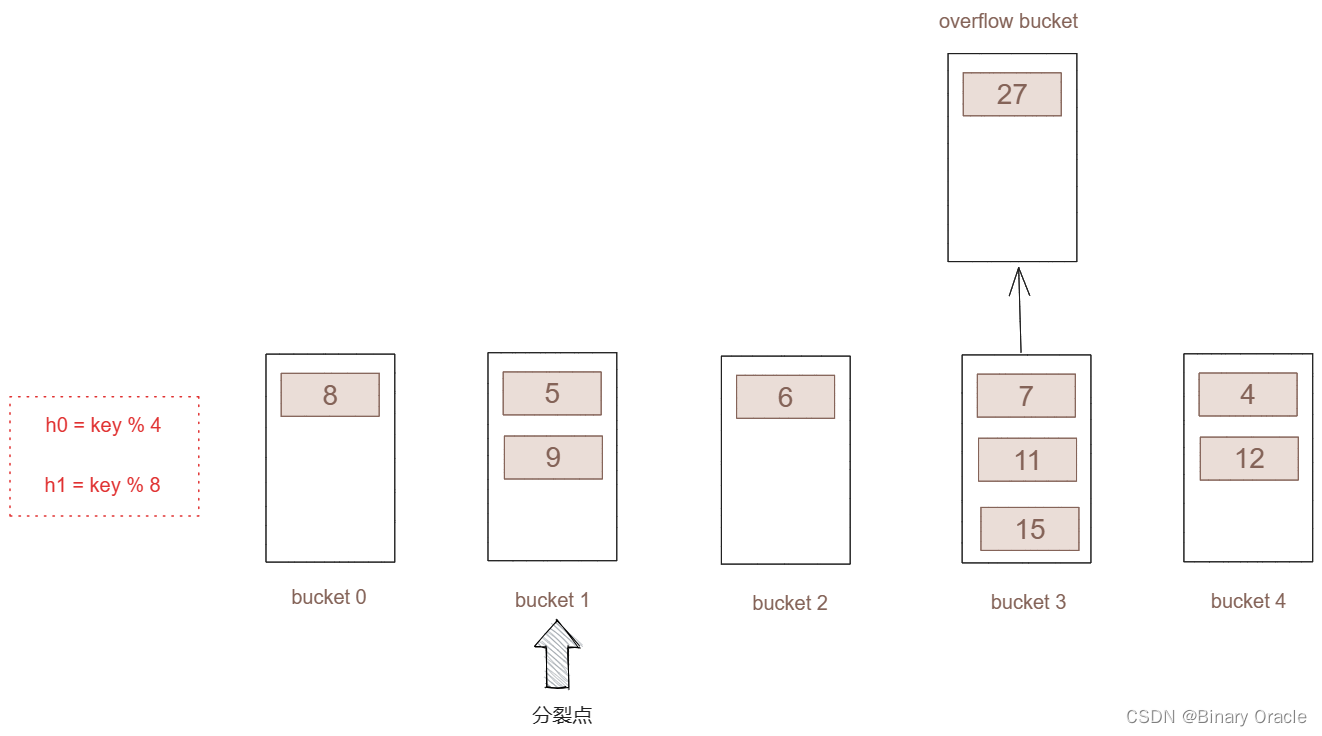
在这里插入图片描述

一次完整的分裂结束

key的读取:

采用h0对key进行计算。
如果算出的桶号小于了分裂点，表示桶已经进行的分裂，我们采用h1进行hash运算，算出key所对应的真正的桶号。再从真正的桶里取出value
如果算出的桶号大于了分裂点，那么表示此桶还没进行分裂，直接从当前桶进行读取value。

说明

如果下一次key插入0、1、2、4桶，是不会触发分裂（没有超出桶的容量）, 如果是插入桶3，用户在实现时可以自己设定，可以一旦插入就触发，也可以等溢出桶达到listSize再触发新的分裂。
现在0桶被分裂了，新数据的插入怎么才能保证没分裂的桶能正常工作，已经分裂的桶能将哪部分插入到新分裂的桶呢?
1. 只要分裂点小于桶的总数，我们依然采用h0函数进行哈希计算。
2. 如果哈希结果小于分裂号，那么表示这个key所插入的桶已经进行了分割，那么我就采用h1再次进行哈希，而h1的哈希结果就这个key所该插入的桶号。
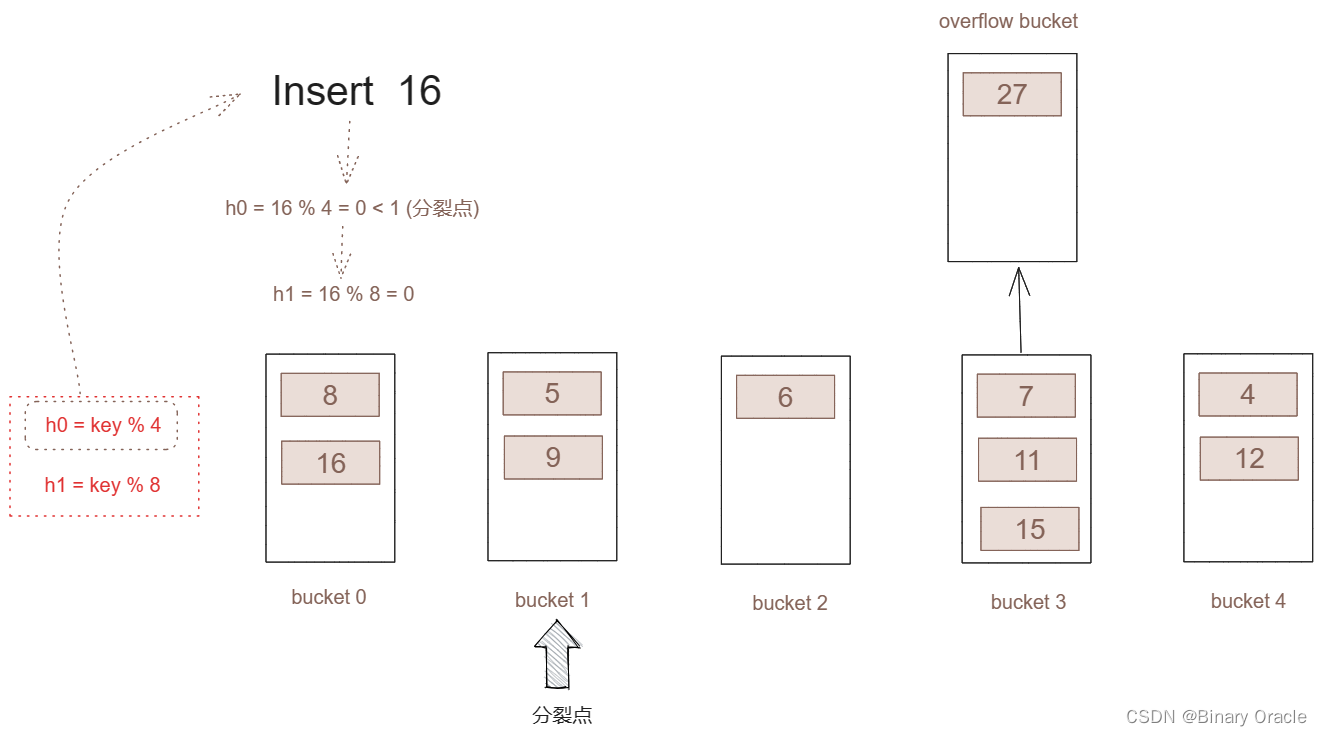
3. 如果哈希结果大于分裂号，那么表示这个key所插入的桶还没有进行分裂。直接插入。
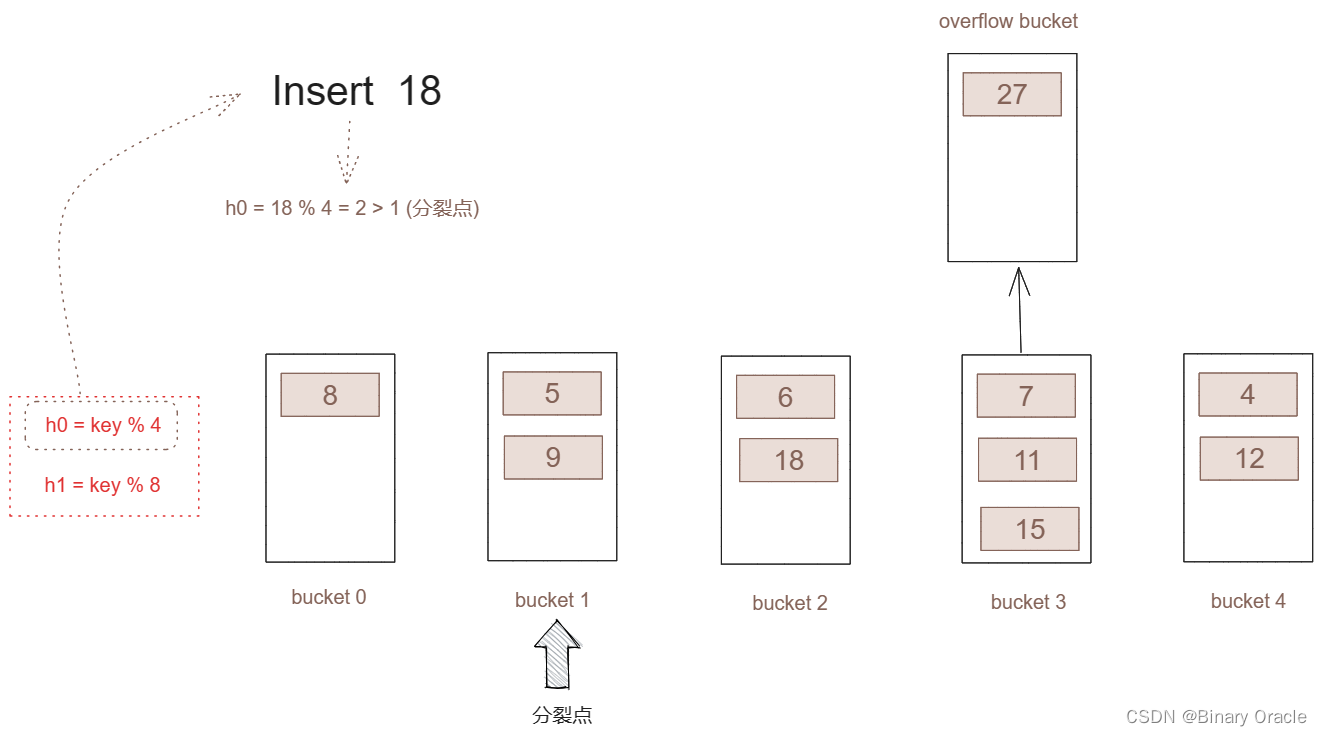
4. 这也是为什么虽然是桶3的容量不足，但分裂的桶是分裂点所指向的桶。如果直接在桶3进行分裂，那么当新的key插入的时候就不能正常的判断哪些桶已经进行了分裂。
如果使用分割点，就具备了无限扩展的能力。当分割点移动到最后一个桶(桶3)。再出现分裂。那么分割点就会回到桶0，到这个时候，h0作废，h1替代h0, h2(key % 12)替代h1。那么又可以开始动态分割。那个整个初始化状态就发生了变化。就好像没有发生过分裂。那么上面的规则就可以循环使用。
线性哈希的论文中是按上面的规则来进行分裂的。其实我们可以安装自己的实际情况来进行改动。

假如我们现在希望去掉分割点，一旦哪个桶满了，马上对这个桶进行分割。

可以考虑了以下方案：

为所有桶增加一个标志位。初始化的时候对所有桶的标志位清空。
一旦某个桶满了，直接对这个桶进行分割，然后将设置标志位。当新的数据插入的时候，经过哈希计算（h0）发现这个桶已经分裂了，那么就采用新的哈希函数(h1)来计算分裂之后的桶号。在读取数据的时候处理类似。

采用此种方案实现的LinerHash简易代码如下所示:

/**
 * lineHash简单实现模型
 */
public class LineHash {
    /**
     * 单桶最多容纳元素个数
     */
    public final int bucketMaxSize;
    /**
     * 分裂点索引
     */
    public int overPoint = 0;
    /**
     * 每一轮的哈希桶数组初始大小
     */
    private int initSize;
    /**
     * 哈希桶数组
     */
    public Bucket[] buckets;

    public LineHash(int bucketMaxSize) {
        this.bucketMaxSize = bucketMaxSize;
        // 初始桶数组大小为4
        buckets = new Bucket[4];
        initSize = 4;
    }

    public String get(int key) {
        int index = calculateIndex(key);
        return buckets[index].get(key);
    }


    public void put(int key, String val) {
        int index = calculateIndex(key);
        Bucket bucket = buckets[index];
        // 判断当前桶是否满了
        if (bucket.size() < bucketMaxSize) {
            bucket.put(key, val);
        } else {
            //满了就进行分裂
            bucket.put(key, val);
            splitHash();
        }
    }

    private int calculateIndex(int key) {
        //根据分裂轮数调用不同的哈希函数
        int index = hashFun(key, 1);
        //当前桶产生了分裂
        if (index < overPoint) {
            //采用新的哈希函数进行计算
            index = hashFun(key, 2);
        }
        lazyInitIfNeed(index);
        return index;
    }

    private void lazyInitIfNeed(int index) {
        if (buckets[index] == null) {
            buckets[index] = new Bucket(bucketMaxSize);
        }
    }

    public int hashFun(int key, int round) {
        return key % (initSize * round);
    }

    public void splitHash() {
        // 待分裂的旧桶
        Bucket oldBucket = buckets[overPoint];
        //分裂产生的新桶
        Bucket newBucket = new Bucket(bucketMaxSize);

        // 对旧桶中的元素进行rehash
        Set<Integer> keySet = oldBucket.keySet();
        List<Integer> removeKeyList=new ArrayList<>(oldBucket.size()/2);
        keySet.forEach(key -> {
            int index = hashFun(key, 2);
            // 说明当前key需要被rehash到新桶中
            if (index >= buckets.length) {
                newBucket.put(key, oldBucket.get(key));
                removeKeyList.add(key);
            }
        });
        removeKeyList.forEach(oldBucket::remove);
        // 将新桶添加进哈希桶数组中
        addBucket(newBucket);
        // 分裂点前移
        overPoint++;
        // 分裂点移动了一轮就更换新的哈希函数
        if (overPoint >= initSize) {
            initSize = initSize * 2;
            overPoint = 0;
        }
    }

    private void addBucket(Bucket newBucket) {
        Bucket[] temp = new Bucket[buckets.length + 1];
        System.arraycopy(buckets, 0, temp, 0, buckets.length);
        temp[buckets.length] = newBucket;
        buckets = temp;
    }

    /**
     * 桶
     */
    private static class Bucket {
        private final Map<Integer, String> map;

        private Bucket(int bucketMaxSize) {
            this.map = new HashMap<>(bucketMaxSize);
        }

        public void put(Integer key, String val) {
            map.put(key, val);
        }

        public String get(Integer key) {
            return map.get(key);
        }

        public int size() {
            return map.size();
        }

        public Set<Integer> keySet() {
            return map.keySet();
        }

        public void remove(Integer key) {
            map.remove(key);
        }
    }
}

这段代码逻辑不完全正确，本人目前能力所限，对liner hash理解还不够透彻，如果有大佬有补充，可以在评论区留言。

关于Linear Hashing的更多内容，大家可以阅读论文学习:

Linear Hashing Paper

spiral storage

Spiral Storage 总是将负载更多的放在哈希表靠前的位置上，而非均匀地将负载分配到整个哈希表中。这样尽管是像 Linear Hashing 一样，总是从哈希表的头部开始进行 bucket 的分裂，也不会有不及时处理非常满的 bucket 的问题。

Spiral Storage 的思路是这样的。哈希表的负载从前向后逐渐降低；扩展大小时，需要将表头的 bucket 中的元素分配到多个新 bucket 中并添加到哈希表的末尾，并且依然保持负载从前向后逐渐下降的性质。假设每去掉表头的一个 bucket 就添加 d 个新 bucket，称 d 为哈希表的增长因子。考虑到哈希表是非线性增加大小的，应该采用一个非线性增长的哈希函数族，将 U 映射到 R。易发现指数函数满足这样的性质。

spiral storage本节讲解的比较模糊，具体可以参考Google的开源实现: