第三章图论 No.11二分图，匈牙利算法与点覆盖

news2024/11/26 20:45:42

文章目录

- 二分+染色：257. 关押罪犯
- 增广路径
- - 372. 棋盘覆盖
- 最小点覆盖
- - 376. 机器任务
- 最大独立集
- - 378. 骑士放置
- 最小路径点覆盖

二分+染色：257. 关押罪犯

257. 关押罪犯 - AcWing题库

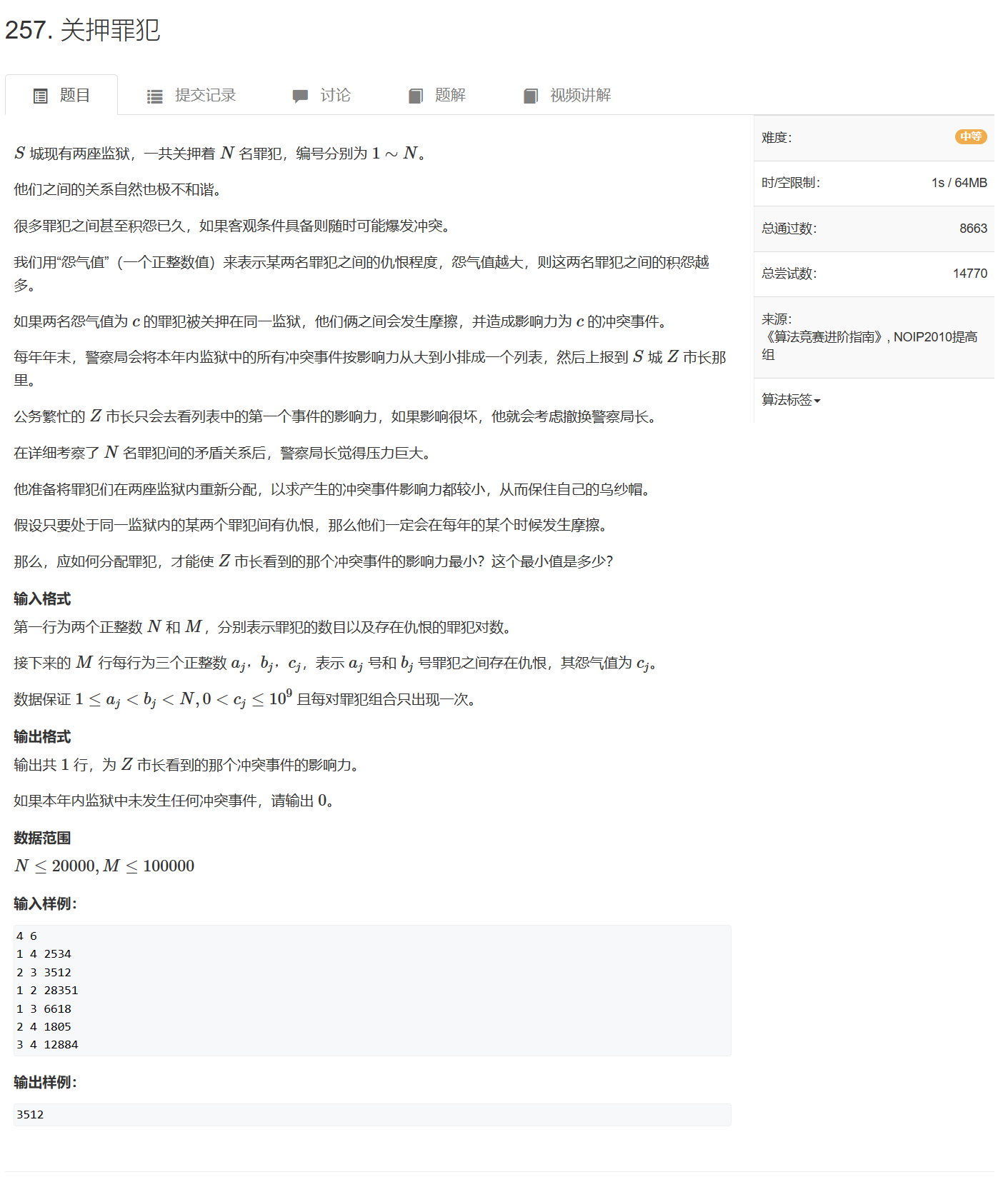
最大最小问题，一眼二分
答案的范围在 $[1, 1 e 9]$ 之间，二分答案，check(mid)
check：将所有权值大于mid的边进行二分，若能得到二分图，返回true，否则返回false
最终将得到最优解ans，所有大于ans的边组成的图为二分图，若是图中有边的权值小于ans，那么这个图就不是二分图
当ans为0时，说明原图就是一张二分图，此时的答案也为0，不需要特判，所以二分的区间为 $[0, 1 e 9]$

#include <iostream>
#include <cstring>
using namespace std;

const int N = 20010, M = 2e5 + 10;
int h[N], e[M], ne[M], w[M], idx;
int color[N];
int n, m;

void add(int x, int y, int d)
{
    e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}

bool dfs(int x, int c, int mid)
{
    color[x] = c;
    for (int i = h[x]; i != -1; i = ne[i])
    {
        if (w[i] <= mid) continue;
        int y = e[i];
        if (!color[y])
        {
            if (!dfs(y, 3 - c, mid)) return false;
        }
        else if (color[y] == c) return false;
    }
    return true;
}

bool check(int mid)
{
    memset(color, 0, sizeof(color));
    for (int i = 1; i <= n; ++ i )
        if (!color[i])
            if (!dfs(i, 1, mid))
                return false;
                
    return true;
}

int main()
{
    memset(h, -1, sizeof(h));
    scanf("%d%d", &n, &m);
    int x, y, d;
    for (int i = 0; i < m; ++ i )
    {
        scanf("%d%d%d", &x, &y, &d);
        add(x, y, d), add(y, x, d);
    }
    
    int l = 0, r = 1e9;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    printf("%d\n", l);
    
    return 0;
}

增广路径

从二分图的非匹配点开始，经过非匹配边，匹配边，非匹配边，匹配边…最后到非匹配点的路径被称为增广路径

将所有匹配边删除，添加非匹配边，图中匹配的对数+1
最大匹配不存在增广路径

372. 棋盘覆盖

372. 棋盘覆盖 - AcWing题库

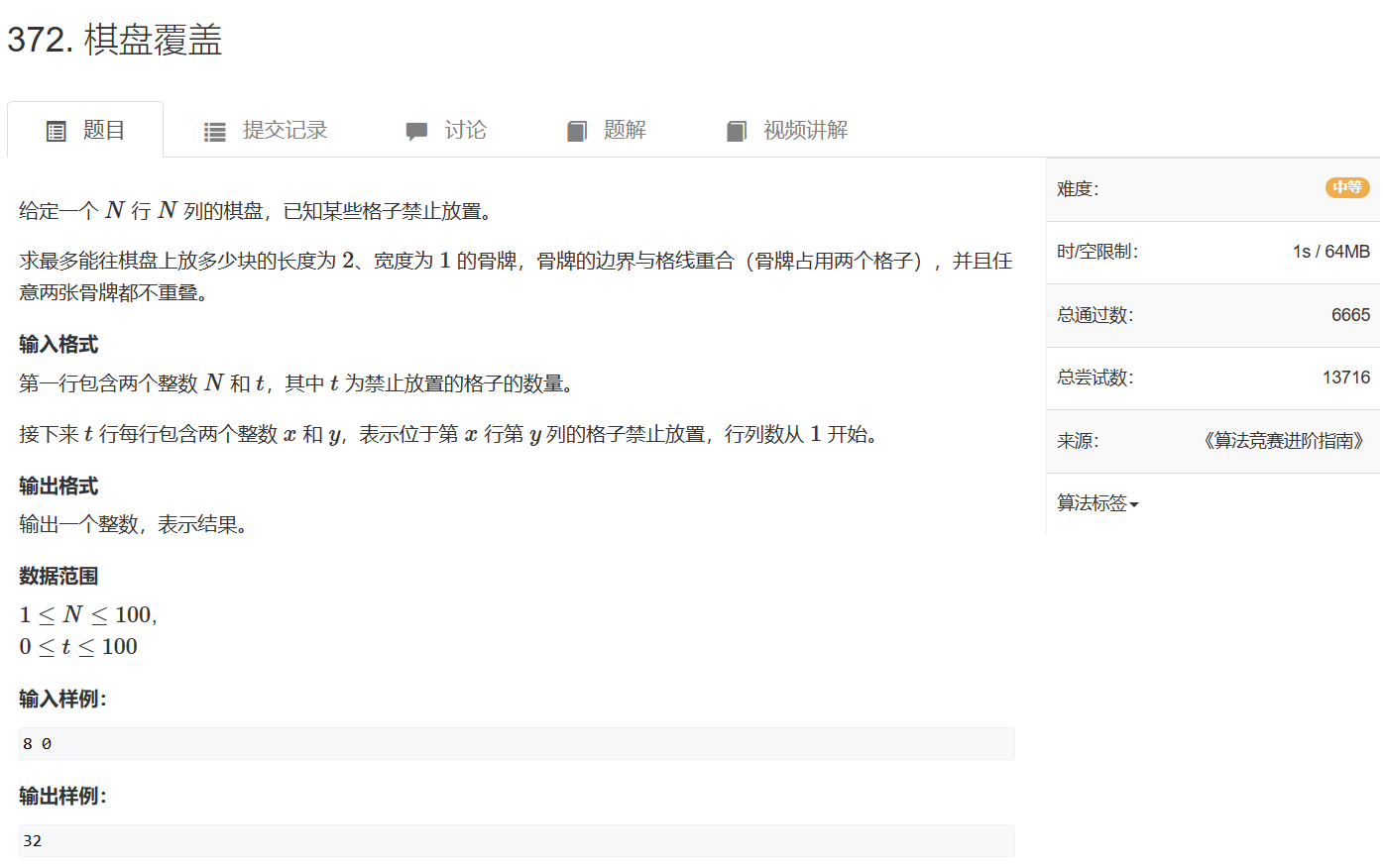
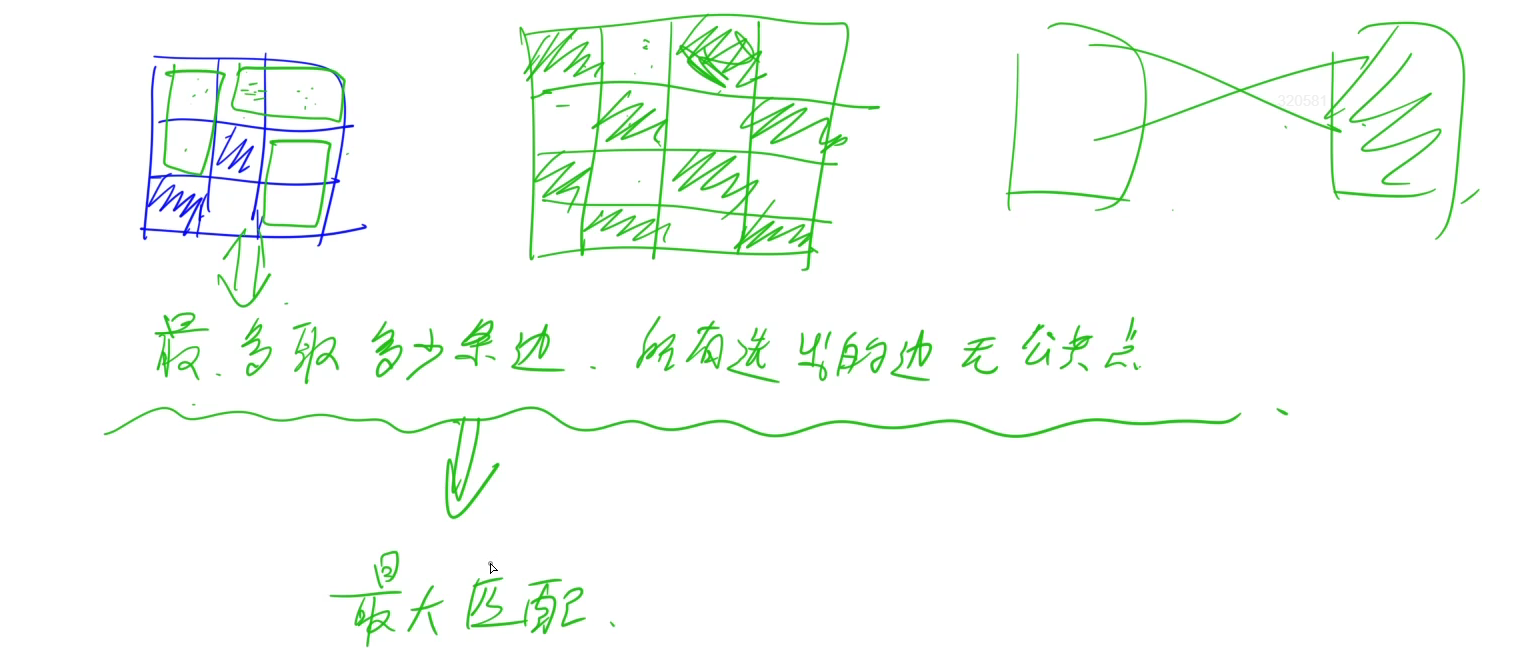
建图方式很特殊，将每个格子看成点，相邻格子之间连一条边，问题就转换成了从图中选择最多的边，使得每条边的点都不重复
这就是一个最大匹配问题
接着判断图是否是一个二分图，若不是二分图，那么不能使用匈牙利算法
将n*m矩阵的奇数格和偶数格（横纵坐标之和）染上不同的颜色，相同颜色的为一组，那么整个矩阵就能被分成两个集合，由于只有相邻格子之间存在边，所以集合中的不存在边，只有集合之间存在边

枚举所有奇数格（或者偶数格），试着将其匹配。注意：不需要枚举坏掉的格子，匹配时也不用匹配坏掉的格子

#include <iostream>
#include <cstring>
using namespace std;

const int N = 110;
typedef pair<int, int> PII;
PII match[N][N];
bool g[N][N], st[N][N];
int dx[4] = { 0, 1, 0, -1 }, dy[4] = { 1, 0, -1, 0 };
int n, m;
    
bool find(int x, int y)
{
    for (int i = 0; i < 4; ++ i )
    {
        int nx = x + dx[i], ny = y + dy[i];
        if (!g[nx][ny] && nx >= 1 && nx <= n && ny >= 1 && ny <= n)
        {
            if (!st[nx][ny])
            {
                auto t = match[nx][ny];
                st[nx][ny] = true;
                if (t.first == 0 || find(t.first, t.second))
                {
                    match[nx][ny] = { x, y };
                    return true;
                }
            }
        }
    }
    return false;
}

int main()
{
    scanf("%d%d", &n, &m);
    int x, y;
    while (m -- )
    {
        scanf("%d%d", &x, &y);
        g[x][y] = true;
    }
    
    
    int res = 0;
    for (int i = 1; i <= n; ++ i )
        for (int j = 1; j <= n; ++ j )
            if ((i + j) % 2 && !g[i][j])
            {
                memset(st, false, sizeof(st));
                if (find(i, j)) res ++ ;
            }
                
    printf("%d\n", res);
    return 0;
}

debug：find的判断条件if (!g[nx][ny] && nx >= 1 && nx <= n && ny >= 1 && ny <= n)的!g[nx][ny]写成了!g[x][y]
每次find之前st数组没有重置

最小点覆盖

给定一个无向图，从中选出最少的点，使得每条边只有一个端点被选择
结论：最小点覆盖 = 最大匹配数

376. 机器任务

376. 机器任务 - AcWing题库

分析题意：有k个任务，每个任务可以在A机器或者B机器上完成，但是机器必须调整为相应的模式，任务的执行顺序任意，求任意顺序中的最少调整次数

建图：将完成每个任务需要调整的模式看成点，一个任务有两个点，在这两点之间连线。显然，得到的图是一个二分图，由于不同任务在相同机器上需要调整的模式可能相同，这些点可以看成一个点
题目要完成所有任务，即选择每条边的一个点，根据题意也就是求最小点覆盖
用匈牙利求二分图的最大匹配即可
由于每台机器的初始状态为0，所以需要调整状态为0的任务不用切换模式，直接就能完成，因此建图时不需要建立这些任务

#include <iostream>
#include <cstring>
using namespace std;

const int N = 210, M = 1010;
int h[N], e[M], ne[M], idx;
int match[N]; bool st[N];
int n1, n2, m;

void add(int x, int y)
{
    e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}

bool find(int x)
{
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int y = e[i];
        if (!st[y])
        {
            st[y] = true;
            if (match[y] == 0 || find(match[y]))
            {
                match[y] = x;
                return true;
            }
        }
    }
    return false;
}

int main()
{
    
    while (scanf("%d", &n1), n1)
    {
        idx = 0;
        memset(h, -1, sizeof(h));
        memset(match, 0, sizeof(match));
        scanf("%d%d", &n2, &m);
        int t, x, y;
        while (m -- )
        {
            scanf("%d%d%d", &t, &x, &y);
            if (x == 0 || y == 0) continue;
            add(x, y);
        }
        
        int res = 0;
        for (int i = 1; i <= n1; ++ i)
        {
            memset(st, false, sizeof(st));
            if (find(i)) res ++ ;
        }
        printf("%d\n", res);
    }
    
    return 0;
}

最大独立集

从一个无向图中选出最多的点，使得选出的点之间都没有边
等价于去掉最少的点，将所有边破坏
等价于最小点覆盖，等价于最大匹配
假设一共n个点，最大匹配数位m，最大独立集的数量为n - m
最大团
从一个无向图中选出最多的点，使得选出的点之间都有边

378. 骑士放置

378. 骑士放置 - AcWing题库

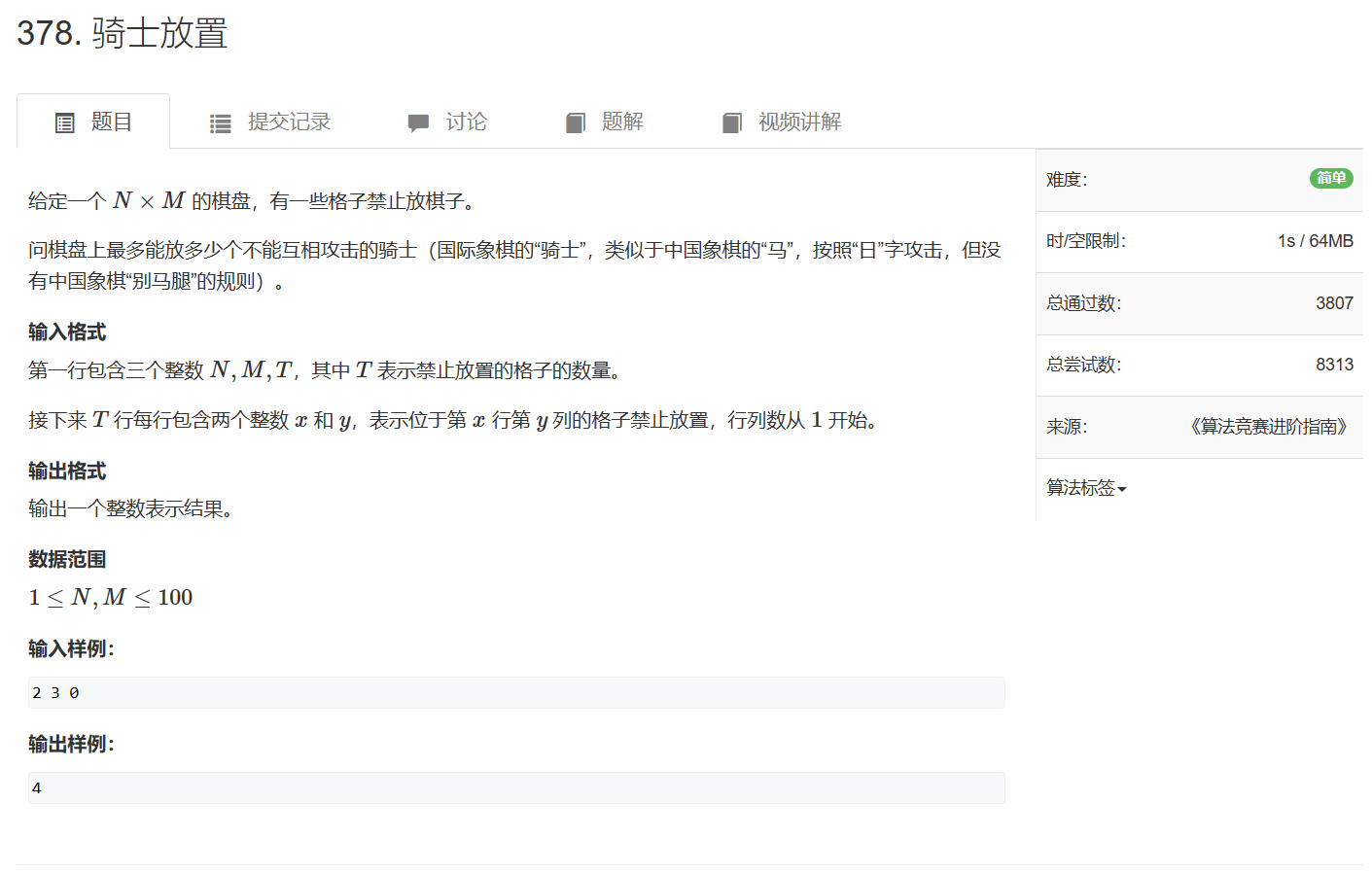
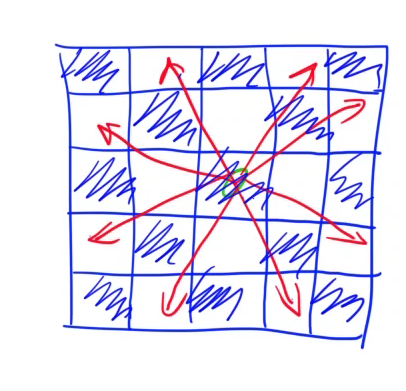
建图：矩阵中，能互相攻击到的格子之间建立一条边
那么问题就转换成了求图的最大独立集，即选择的格子之间都没有边，不能相互攻击

验证建的图是否为二分图，将奇数格和偶数格染不同的颜色，若当前坐标为 $(x, y)$ ，那么该坐标之和为 $x + y$ ，要得到与之相连的坐标，就要将x±1，y±2，坐标之和要±一个奇数
假设坐标之和为奇数，加上奇数得到偶数，格子的颜色不同
假设坐标之和为偶数，加上奇数得到奇数，格子的颜色也不同
所以该图是一个二分图，可以使用匈牙利算法求最大匹配

#include <iostream>
#include <cstring>
using namespace std;

typedef pair<int, int> PII;
const int N = 110;
bool g[N][N], st[N][N];
PII match[N][N];
int dx[8] = { 1, 1, 2, 2, -1, -1, -2, -2 }, dy[8] = { 2, -2, 1, -1, 2, -2, 1, -1 };
int n, m, t;

bool find(int x, int y)
{
    for (int i = 0; i < 8; ++ i )
    {
        int nx = x + dx[i], ny = y + dy[i];
        if (!g[nx][ny] && nx >= 1 && nx <= n && ny >= 1 && ny <= m)
        {
            if (!st[nx][ny])
            {
                st[nx][ny] = true;
                auto t = match[nx][ny];
                if (t.first == 0 || find(t.first, t.second))
                {
                    match[nx][ny] = { x, y };
                    return true;
                }
            }
        }
    }
    return false;
}

int main()
{
    scanf("%d%d%d", &n, &m, &t);
    int x, y;
    for (int i = 0; i < t; ++ i )
    {
        scanf("%d%d", &x, &y);
        g[x][y] = true;
    }
    int res = 0;
    for (int i = 1; i <= n; ++ i )
        for (int j = 1; j <= m; ++ j )
            if (!g[i][j] && (i + j) % 2)
            {
                memset(st, 0, sizeof(st));
                if (find(i, j)) res ++ ;
            }
            
    printf("%d\n", n * m - t- res);
    return 0;
}