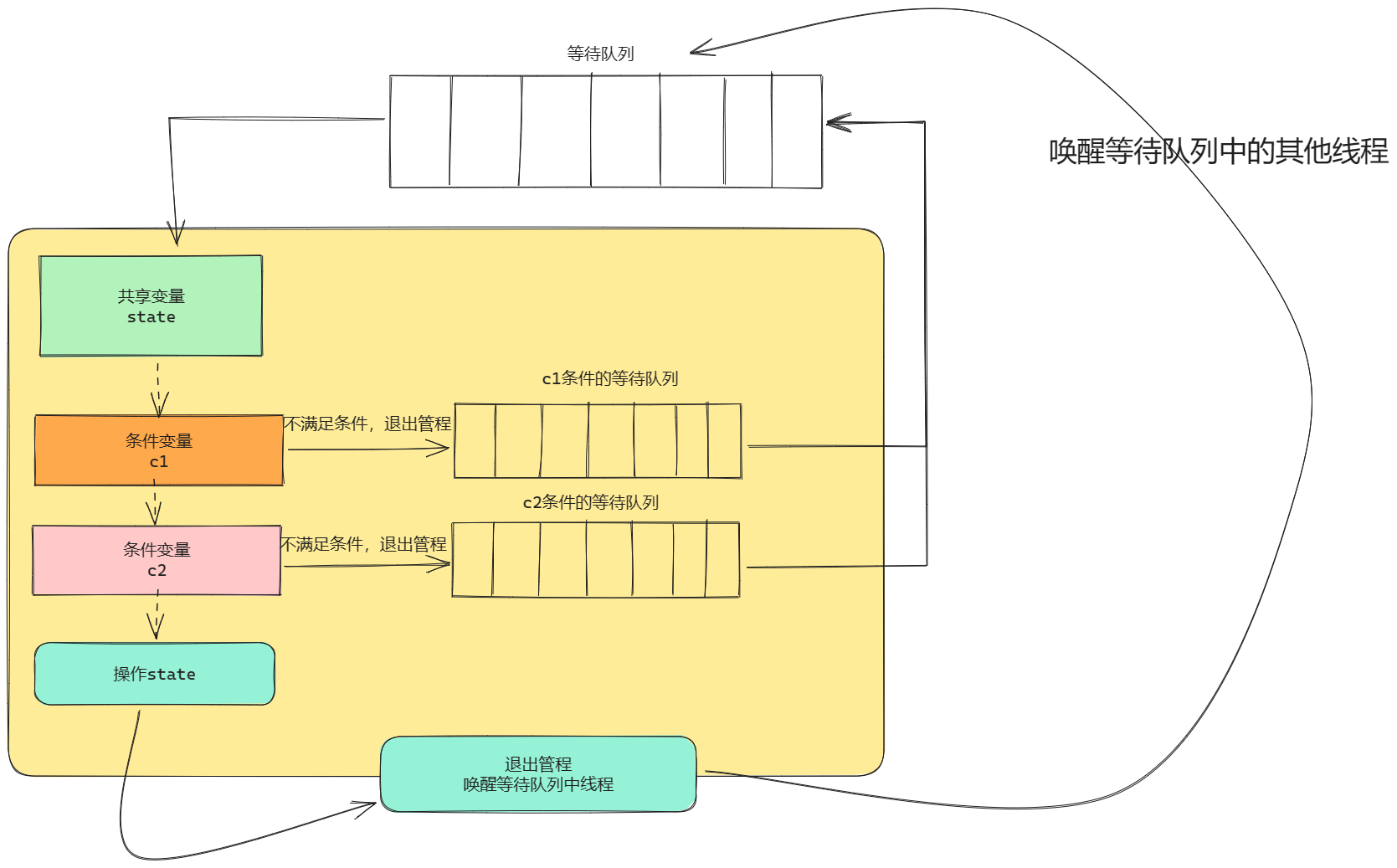
单目初始化
1.前提条件(640*480)
- 参与初始化的两帧各自的特征点数目都需要大于100.
- 两帧特征点成功匹配的数目需要大于或等于100.
- 两帧特征点三角化成功的三维点数目需要大于50.
2.针对条件三 流程如下
- 记录当前帧和参考帧(第一帧)之间的特征匹配关系。
- 在特征匹配点对中随机选择8对匹配点作为一组。
- 对这8对点分别计算基础矩阵F和单应矩阵H,并得到得分。
- 计算得分比例,根据判断选择基础矩阵还是单应矩阵求位姿和三角化。
3. 求单应矩阵--平面
- 对特征匹配点坐标进行归一化。
- 开始迭代,每次选择8对点计算单应矩阵。
- 根据当次计算的单应矩阵的重投影误差对结果进行评分。
- 重复2、3步,以得分最高的单应矩阵作为最优的单应矩阵。
3.1坐标归一化
目的:防止坐标值量级差别较大。
好处:能够提高运算结果的精度;利用归一化处理后的图像坐标,对尺度缩放和原点的选择不敏感。
归一化操作步骤如下:
1.计算每个特征点坐标分别在两个坐标轴方向上的均值meanX,meanY
2.求出平均到每个点上,其坐标偏离均值meanX、meanY的程度,记为meanDevX,meanDevY,并将其倒数作为一个尺度缩放因子sX,sY。
3.用均值和尺度缩放因子对坐标进行归一化
4.用矩阵表示上述变换关系,得到归一化矩阵T
归一化代码如下:
3.2求解单应矩阵
单应矩阵H的自由度是8,一对特征点可以提供两个约束方程,所以只需要4对点提供8个约束方程就可以求解了。
为什么自由度是8?因为Ah=0,矩阵H共有9个元素,去掉一个自由度,就是8个自由度。

对矩阵A进行SVD分解

代码:
3.3检验单应矩阵并评分
通过单应矩阵对已经判断为内点的特征点进行双向投影,计算加权重投影误差,最终选择误差最小的单应矩阵作为最优解。
特征点对之间双向投影,累计所有特征点对中的内点误差,误差越大评分越低。
4.求基础矩阵F--非平面
- 对特征匹配点坐标进行归一化
- 选择8个点对来计算基础矩阵。
- 根据当次计算的基础矩阵的重投影误差对结果进行评分。
- 重复2、3步,以得分最高的基础矩阵作为最优的基础矩阵。
4.1使用八点法求解基础矩阵
基础矩阵共有9个元素,其中尺度等价性去掉1个自由度,基础矩阵秩为2,再去掉1个自由度,所以自由度应该为7.

SVD求解基础矩阵