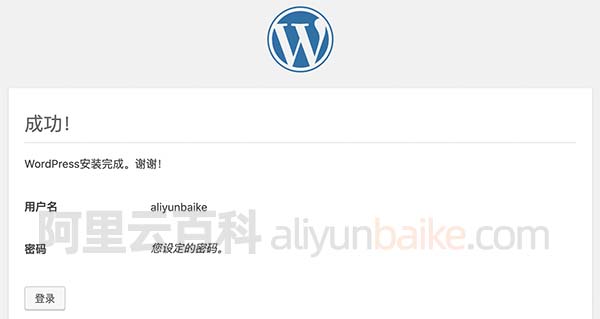
发生数据丢失的原因有多种。无论是因为文件被意外删除、文件系统或操作系统损坏，还是由于软件或硬件级别的存储故障，数据都会在您最意想不到的时候丢失。今天我们重点介绍五种数据恢复方法，以应对意外情况的发生。
1.从另一台机器启动硬盘
如果 Windows 无法加载，请将硬盘从有问题的计算机中取出。现在，要么将其作为从属设备安装在另一台工作机器中，要么将其放入外部驱动器外壳中。目标是使驱动器在 Windows 资源管理器中显示为另一个驱动器号，以便您查看驱动器的内容并挑选出所需的数据。
2.使用数据恢复工具
从 Windows 操作系统恢复已删除数据的最简单、最快的方法之一是使用数据恢复工具。像奇客数据恢复这样的应用程序 可以让您在几分钟内从多个文件系统中恢复丢失的数据。前面提到的 PhotoRec 需要更多的人力，但功能非常强大，可以从 FAT、NTFS、ext 和 HFS+ 文件系统恢复 400 多种文件类型。
奇客数据恢复: 支持1000+数据格式恢复免费下载软件扫描数据，支持文件、照片、视频、邮件、音频等1000+种文件的格式恢复更有电脑/笔记本、回收站、U盘、硬盘等各类存储设备数据丢失恢复
https://www.geekersoft.cn/geekersoft-data-recovery.html对于分区损损坏造成数据丢失的情况，请尝试奇客数据恢复。奇客数据恢复的主要目标是帮助恢复丢失的分区数据，但也用于从 FAT、exFAT、NTFS 和 ext2 分区恢复已删除的文件。
3. 使用可启动的 Live CD/USB
同样，如果您想在有问题的计算机上绕过 Windows 并访问数据本身，您可以使用 Live CD/USB。这将使您能够将数据保存到网络或外部 USB 驱动器。基于 Linux 的可启动操作系统（例如 DEFT 或 Ubuntu） 就是此类 Live CD/USB 的两个示例。
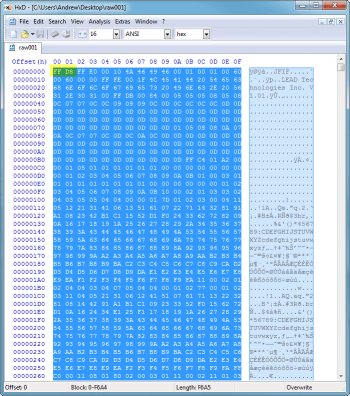
4.使用十六进制编辑器
十六进制编辑器（例如 HxD Hex Editor）可以让您访问“原始”（十六进制）格式的数据。当您使用分区损坏且文件元数据丢失的硬盘时，这非常有用。如果您知道需要恢复的文件类型的结构，则可以使用 SOF（文件开始）标记或页眉和 EOF（文件结束）标记或页脚来手动提取数据并将其保存为正确的文件格式。
注意：如果硬盘已加密，此方法将不起作用。
在下面的示例中，我搜索了 FF D8 的十六进制数据，一直到 FF D9（JPEG 文件的页眉和页脚），并将该数据导出到文件中。一旦我给它一个 .jpg 扩展名，我就可以打开它并看到一张照片。
5. 编写脚本自动刻出文件
使用与上述相同的概念，您还可以编写自己的脚本来扫描原始硬盘驱动器映像并自动提取数据。这种脚本的基本逻辑如下：
寻找 SOF 标记
寻找 EOF 标记
将 SOF 和 EOF 标记之间的数据保存到文件
为文件指定适当的文件类型扩展名
如果您想查看现成的文件雕刻器，请尝试 PhotoRec 或 Scalpel，它们都是开源的。这些有助于帮助您练习和理解数据雕刻的基本概念。
结论
尽管知道如何恢复数据有明显的好处，但在这些情况下主动而不是被动通常被认为是更明智的方法。
如果预算允许，没有什么比拥有一个 实时备份解决方案 更好的了，它可以快速恢复数据并避免首先需要恢复数据的麻烦。这样的解决方案将允许您通过单击按钮将文件恢复到原始计算机上或网络上的另一台计算机上的原始状态。
