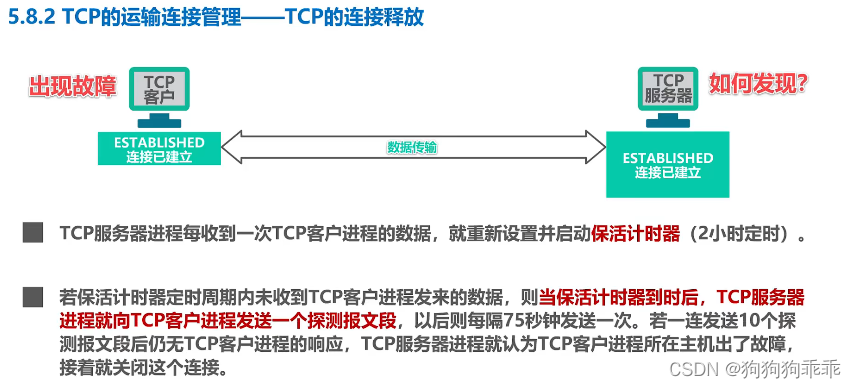
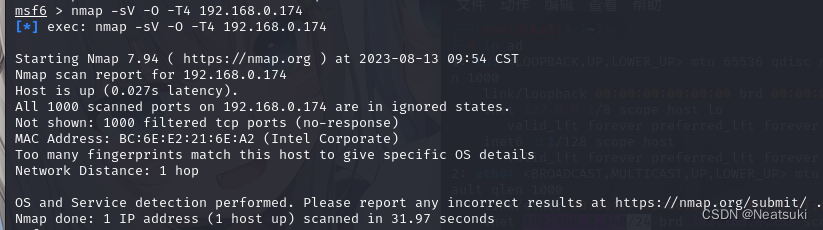
是一个基于动态规划的全源最短路算法。它可以高效地求出图上任意两点之间的最短路

时间复杂度 O(n^3)

状态转移方程

f[i][j]=min(f[i][j],f[i][k]+f[k][j])

核心代码 

void floyd(){
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				s[i][j]=min(s[i][j],s[i][k]+s[k][j]);
}

k就是一个中间值，每次把从i到j的距离与从i到k再从k到j的距离进行比较，选取最小值，做答案

 例如k等于1的时候可以更新4，2这个点k等于2的时候可以更新3，1这个点。。。。。。

例题B3647 【模板】Floyd 算法

给出一张由 n 个点 m 条边组成的无向图。

求出所有点对 (i,j) 之间的最短路径。

输入格式

第一行为两个整数 n,m，分别代表点的个数和边的条数。

接下来 m 行，每行三个整数 u,v,w，代表 u,v 之间存在一条边权为 w 的边。

输出格式

输出 n 行每行 n 个整数。

第 i 行的第 j 个整数代表从 i 到 j 的最短路径。

输入输出样例

输入 

4 4
1 2 1
2 3 1
3 4 1
4 1 1

输出 

0 1 2 1
1 0 1 2
2 1 0 1
1 2 1 0

说明/提示

对于 100% 的数据n≤100,m≤4500，任意一条边的权值 w 是正整数且 1⩽w⩽1000。

#include<iostream>
using namespace std;
const int N=1e4,INF=1e9;
int s[N][N];     //用于存图
int n,m,q;

void floyd(){
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				s[i][j]=min(s[i][j],s[i][k]+s[k][j]);
}

int main(){
	cin>>n>>m;
	//初始化
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)  
			if(i==j)s[i][j]==0;
			else s[i][j]=INF;     //s[i][j]代表从i到j的最短距离
			
	//把给的边存入
	while(m--){
		int a,b,c;
		cin>>a>>b>>c;
		s[a][b]=min(s[a][b],c);
		s[b][a]=min(s[b][a],c);    //可能给重复的值，取最小的那一个存入 
	} 
	
	floyd();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++)
			cout<<s[i][j]<<" ";
			cout<<endl;
    }
	return 0;
}