文章目录

前言

1. 题目：设计循环队列

2. 思路

3. 分析

3.1 定义循环队列

3.2 创建队列

3.3 判空和判满

3.4 入队

3.5 出队

3.6 取队头队尾数据

3.7 销毁队列

4. 题解

总结

前言

当谈到队列数据结构时，很多人可能会想到普通的队列，即先进先出（FIFO）的数据结构。然而，有时候我们需要一种更高效的队列实现方式，这就是循环队列。

1. 题目：设计循环队列

题目描述：

题目链接：

设计循环队列https://leetcode.cn/problems/design-circular-queue/

2. 思路

先来理解一下题意，首先队列的长度为定长k，其次就是队列可以循环利用空间。这里我们要思考一下是使用链表实现，还是使用数组实现。在设计这个环形队列的时候，我们肯定是要设计头和尾的入下图：

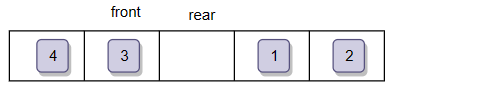
当前状态视为队列满，这时如果出队元素就会空出空间此时我们可以继续入队数据如下图：

后边满了以后再插入数据它可以绕回来，这就是循环队列。从front开始道rear结束就是队列的数据。或许有人会有疑惑：为什么不把尾指向最后一个元素，而是指向最后一个元素的后一个位置？

这样是为了便于判断队列是否为空，我们举个例子，队列为空时front和rear是都指向开头的，如果插入一个数据，rear就要向后移动，不移动就无法判断队列是否为空。

接下来我们回到开始的问题，使用数组还是链表实现？

我们依据上一个问题，知道rear指向的是队尾的后一个元素，那依据单链表的特性取队尾不好取。如果要好取尾就要用双向循环链表会好搞一些，当然还有其他的解决办法例如：多加一个变量size记录队列数据个数，rear指向队尾，这样也可以解决，但这样写代码会很容易让人误导，所以这里不推荐这样的方法。链表实现也是可以的，但相对数组的代码量就比较多了。使用数组实现也会简单方便的多。

数组：

当rear+1==front时就是为满，由于它是一个循环队列，rear在末尾后再+1就会回到头，这里可以写成这样：front==（rear+1）%（k+1）（取值范围0~k），它要始终保持front与rear之间留有一个空。这里我们就使用数组来实现。

3. 分析

依据上述的思路，我们使用数组来实现循环队列，通过上述的思路我们可以发现这个规律，出队就front向后走，入队就rear向后走。

3.1 定义循环队列

typedef struct {
    int* a;
    int front;
    int rear;
    int k;
} MyCircularQueue;

a用于存放数据，和顺序表类似，使用malloc开辟空间。front为队头，rear为队尾。

3.2 创建队列

MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));

    //多开一个空间
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->front=obj->rear=0;
    obj->k=k;

    return obj;
}

这里和之前一样，我们仅仅是定义了队列的类型，并没有创建结构体变量，为了便于后续传参，这里我们使用malloc创建一个结构体变量。有了obj就可以通过它来找到结构体中的各个成员。注意我们还需要对数组a进行开辟空间。

3.3 判空和判满

这里我们先来实现判满和判空操作，上述思路中我们多开辟一个空间，用于判断满和空的情况，如果rear等于front就为空，如果rear+1等于front就为满。接下来我们来实现一下：

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return (obj->front==obj->rear);
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->front==(obj->rear+1));
}

但这样写对吗？这样写是不对的，前边思路中提到：front==（rear+1）%（k+1）为了达到返回开头的目的，所以这里需要改写（也是为了防止rear+1越界）。

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return (obj->front==obj->rear);
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->front==(obj->rear+1)%(obj->k+1));
}

这里可能就有人疑惑了，为什么rear需要模k+1返回，front就不需要呢？front也会走到尾啊。

这个当然是需要考虑的，这个操作是在出队操作时考虑的，在判满时可以不考虑，满的情况分为两种：

第一种：

第二种：

3.4 入队

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
        return false;

    obj->a[obj->rear]=value;
    obj->rear++;

    obj->rear%=(obj->k+1);
    return true;
}

入队操作非常简单，在入队之前先判断队是否满，如果满直接返回false（错误）。不为满就将rear位置入队数据，然后rear向后移动，这里为了便于rear返回，这里rear需要%=（k+1）。

过程如下：

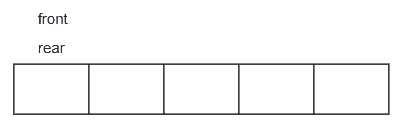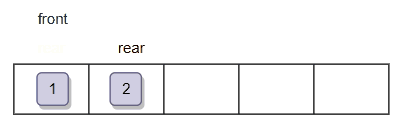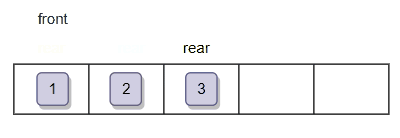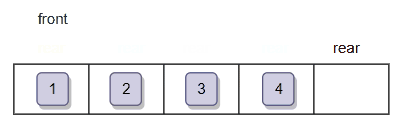
3.5 出队

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return false;

    obj->front++;
    obj->front %=(obj->k+1);
    return true;
}

出队前要先判断队列是否为空，不为空就front++即可不需要任何修改（front开始到rear直接的为有效数据），为了便于front返回，这里可以使用取模，或者使用if语句判断，都可以。

再次入队数据就会将原数据自动覆盖。

3.6 取队头队尾数据

取队头数据非常简单

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[obj->front];
}

如果为空就直接返回-1，如果不为空就返回数组front下标的数据。重点在于队尾数据。

一般情况队尾数据只需要rear-1就可以了，但是这里需要考虑rear为0的情况。如果rear为0，rear-1就越界非法访问了，我们需要的是rear返回到数组最后的位置。这里我们可以这样操作，既然我们是取模让rear达到返回到0，那我们在对rear取模之前先对rear+（k+1），这样rear取模后仍然可以取到下标为0的位置，-1就回到了最后的位置（减一后：（rear+k）%（k+1）结果为k）。

（rear+（k+1）-1）%k+1化简一下就是：（rear+k）%（k+1），代码实现：

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[(obj->rear+obj->k)%(obj->k+1)];
}

3.7 销毁队列

销毁队列也非常简单，先销毁啊数组，再销毁obj。

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

4. 题解

整体代码：

typedef struct {
    int* a;
    int front;
    int rear;
    int k;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->front=obj->rear=0;
    obj->k=k;
    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return (obj->front==obj->rear);
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->front==(obj->rear+1)%(obj->k+1));
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
        return false;

    obj->a[obj->rear]=value;
    obj->rear++;

    obj->rear%=(obj->k+1);
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return false;

    obj->front++;
    obj->front %=(obj->k+1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[(obj->rear+obj->k)%(obj->k+1)];
}



void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

力扣上边也是可以通过的。