matlab解常微分方程常用数值解法2：龙格库塔方法

news2024/11/24 0:55:52

总结和记录一下matlab求解常微分方程常用的数值解法，本文将介绍龙格库塔方法（Runge-Kutta Method）。

龙格库塔迭代的基本思想是：

$x_{k+1}=x_{k}+a k_{1}+b k_{2}$

$k_{1}=h f\left(x_{k},t_{k} \right) \quad \text { and } \quad k_{2}=h f\left(x_{k}+B_{1}k_{1},t_{k}+A_{1} h \right)$

其中 $a,b,A_1,B_1$ 是未知的，我们进行推导。

首先对 $f (x + k, t + h)$ 进行泰勒展开：

$\begin{aligned} f(x+k, t+h) & =f(x, t)+\left(k f_{x}+h f_{t}\right)+\frac{1}{2}\left(k^{2} f_{xx}+2 k h f_{xt }+h^{2} f_{tt}\right) \\ & +\frac{1}{6}\left(k^{3} f_{xxx}+3 k^{2} h f_{xxt}+3 k h^{2} f_{xtt}+h^{3} f_{ttt}\right)+\cdots \end{aligned}$
利用泰勒展开我们展开 $k_2$ ：
$\begin{aligned} k_{2} & =h f\left[x_{k}+B_1 h f\left( x_{k},t_{k}\right),t_{k}+A_{1} h\right] \\ & =h\left[f\left(x_{k},t_{k} \right)+\left(B_{1} h f f_{x}+A_{1} h f_{t}\right)\right] \\ & =h f+A_{1} h^{2} f_{t}+B_{1} h^{2} f f_{x}, \end{aligned}$
上式中的 $f$ 为 $f(x_k,t_k)$ ，我们将上式代回到最开始的式子 $x_{k+1}=x_{k}+a k_{1}+b k_{2}$ 得到(*)式

$x_{k+1}=x_{k}+(a+b) h f+\left(A_{1} b f_{t}+B_{1} b f f_{x}\right) h^{2}\quad\quad(*)$

对应于二阶泰勒展式：

$x_{k+1}=x_{k}+h x_{k}^{\prime}+\frac{1}{2} h^{2} x_{k}^{\prime \prime}$

对于微分方程我们知道 $x^{\prime}=f(x, t)$ ，于是对 $t$ 求二阶导数：

$x^{\prime \prime}=f_{t}+f_{x} x^{\prime}=f_{t}+f f_{x}$

于是有：

$x_{k+1}=x_{k}+h f+\frac{1}{2} h^{2}\left(f_{t}+f f_{x}\right)$

对比(*)式我们有：

$A_{1} b=\frac{1}{2}, \quad \text { and } \quad B_{1} b=\frac{1}{2} \text {. }$

如果我们取 $a=b=\frac{1}{2}$ ，那么 $A_1=B_1=1$ ，为二阶的龙哥库塔算法。其形式和改进的欧拉法一致:

$x_{k+1}=x_{k}+\frac{1}{2}\left(k_{1}+k_{2}\right)$

从二阶的出发，我们可以得到改进的一套更好的框架，一个常用的龙哥库塔方法是四阶的：

$x_{k+1}=x_{k}+\frac{1}{6}\left(k_{1}+2 k_{2}+2 k_{3}+k_{4}\right) \text {, }$

其中：

$\begin{aligned} &k_{1}=h f\left(x_{k},t_{k} \right) \\ &k_{2}=h f\left(x_{k}+\frac{1}{2} k_{1},t_{k}+\frac{1}{2} h \right) \\ &k_{3}=h f\left(x_{k}+\frac{1}{2} k_{2},t_{k}+\frac{1}{2} h \right) \\ &k_{4}=h f\left(x_{k}+k_{3},t_{k}+h\right) \end{aligned}$

例子

$x^{\prime}=x+t, \quad x(0)=1$

clc
clear
% 测试4个不同的步长
test_times = 3;
h_test = [0.10, 0.05, 0.01];%根据步长数改变

% 保存时间、差分时间和步长
h_res=ones(1,test_times);
t_res=cell(1,test_times);%时间
tplot_res=cell(1,test_times);%差分的时间，比时间长度少1
% 保存两种数值方法和解析解的计算结果
x_rk_res=cell(1,test_times);
x_exact_res=cell(1,test_times);
% 保存误差
diff_res=cell(1,test_times);



for i = 1:test_times
% 设置步长间隔和步长数
    h = h_test(i);
    n = 10/h;
% 设置初始条件
    t=zeros(n+1,1); t(1) = 0;
    x_rk=zeros(n+1,1); x_rk(1) = 1;
    x_exact=zeros(n+1,1); x_exact(1) = 1;
% 设置龙哥库塔方法误差存放向量（和精确解比较）
    diff = zeros(n,1); tplot = zeros(n,1);
% 定义微分方程
    f = @(tt,xx)(xx+tt);
    for k = 1:n
        x_local = x_rk(k); t_local = t(k);
        k1 = h * f(t_local,x_local);
        k2 = h * f(t_local + h/2,x_local + k1/2);
        k3 = h * f(t_local + h/2,x_local + k2/2);
        k4 = h * f(t_local + h,x_local + k3);
        t(k+1) = t_local + h;
        x_rk(k+1) = x_local + (k1+2*k2+2*k3+k4) / 6;
        x_exact(k+1) = 2*exp(t(k+1)) - t(k+1) - 1;
        tplot(k) = t(k);
        diff(k) = x_rk(k+1) - x_exact(k+1);
        diff(k) = abs(diff(k) / x_exact(k+1));
    end
    diff_res{i}=diff;
	tplot_res{i}=tplot;
	h_res(i)=h;
	x_rk_res{i}=x_rk;
	x_exact_res{i}=x_exact;
	t_res{i}=t; 
end

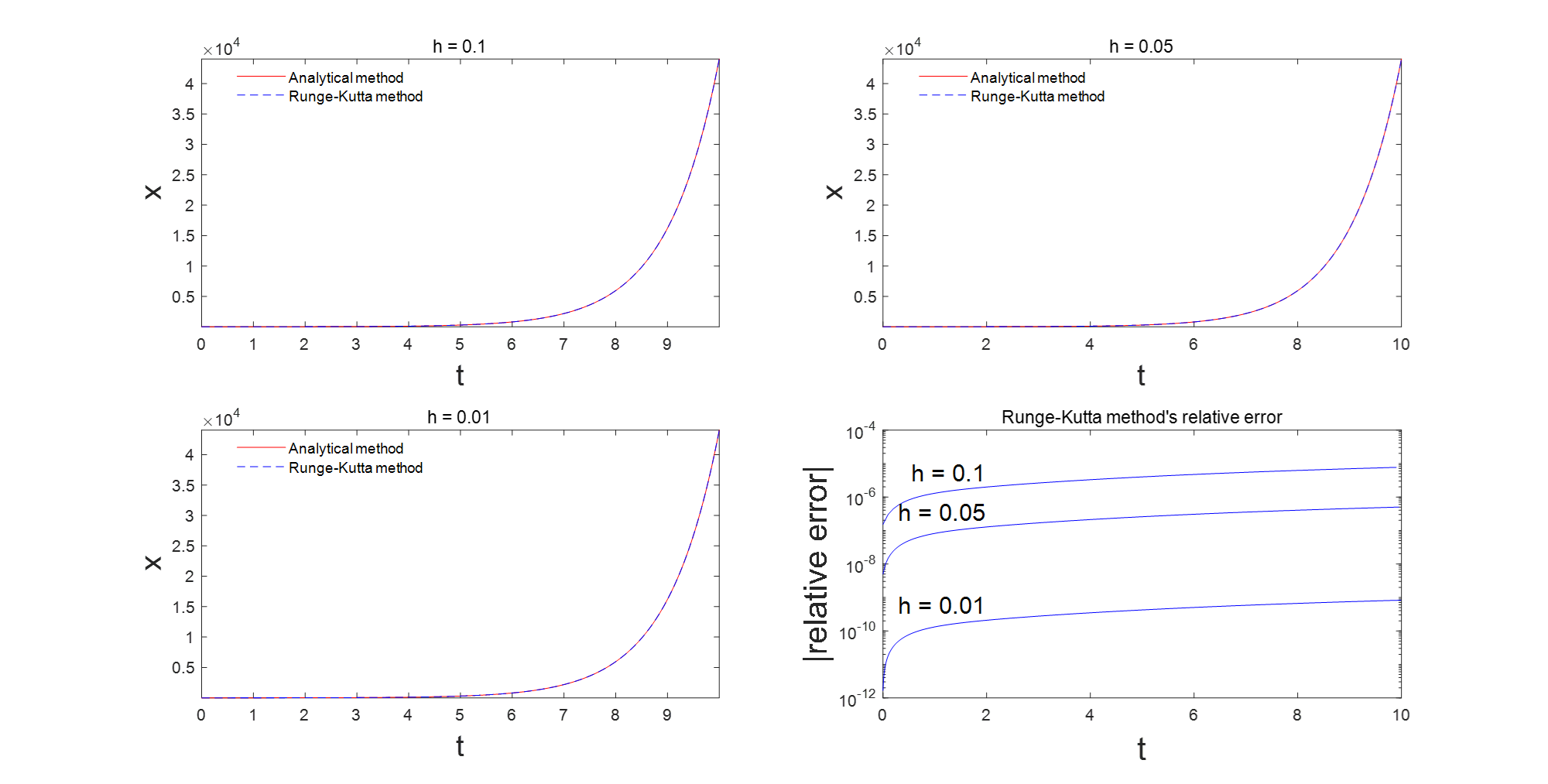
figure
% 不同步长下的解析解和龙哥库塔法的结果
for i=1:test_times
    subplot(2,2,i)
    plot(t_res{i},x_exact_res{i},'r-',t_res{i},x_rk_res{i},'b--')
    xlabel('t','Fontsize',18)
    ylabel('x','Fontsize',18)
    legend({'Analytical method','Runge-Kutta method'},'Location','best')
    legend boxoff;
    title(['h = ',num2str(h_res(i))]);
    axis tight
end

% 相对误差图
subplot(2,2,4)
for i = 1:test_times
    semilogy(tplot_res{i},diff_res{i},'b-')
    hold on
    num1 = 2; num2 = 2/h_test(i);
    text(num1,diff_res{i}(num2),['h = ',num2str(h_res(i))],'Fontsize',15,...
    'HorizontalAlignment','right',...
    'VerticalAlignment','bottom')
end
xlabel('t','Fontsize',20)
ylabel('|relative error|','Fontsize',20)
title('Runge-Kutta method''s relative error')