ACL 2023 | 使用语言模型解决数学推理问题的协同推理框架

©PaperWeekly 原创 · 作者 | 朱欣宇

单位 | 清华大学

研究方向 | 自然语言处理

论文标题：

Solving Math Word Problems via Cooperative Reasoning induced Language Models

论文链接：

https://arxiv.org/abs/2210.16257

代码链接：

https://github.com/TianHongZXY/CoRe

Language Models 解决推理任务

过去的一年里，使用语言模型来解决各种各样的推理问题变成了一个非常火热的研究课题，出现了许多非常简单，但效果惊人的方法，特别是以 Chain of Thought [1]（CoT）系列为代表的 prompt design 工作。

后续的改进工作层出不穷，比如将原始 CoT 中的构建 few-shot 例子所需的人工成本降为只需要一句 “Let's think step by step” 的 Zero-shot CoT [2]，使用聚类方法自动化构建 few-shot 例子的 auto-CoT [3]，这些 prompt + Large Language Models（LLMs）的工作可以说掀起了使用 LLMs 做推理任务的热潮。

然而，这些工作的惊人效果很大程度上依赖于 LLMs 本身的强大能力，正如 CoT 原文中指出的那样，在较小的语言模型（< 10B 参数）上，CoT 的提升并不明显，甚至有下降。Chain of Thought hub [4] 中的排行榜也清晰地指出了开源模型与 OpenAI，Anthropic 的闭源模型在复杂推理任务（特别是数学推理）上的差距，正如项目主页中写的那样：“chit-chat is cheap, show me the reasoning”。

尽管也有一些专注于提升较小的语言模型推理能力的工作，如 STaR [5]，但是这种提升仅在相对简单的常识推理任务上较为明显，在难度更大的数学推理上，比如知名的 GSM8K 数据集，提升效果并不理想，使用一个 6B 参数的 GPT-J，仅能达到 10.7 的 accuracy，与 CoT + LLMs 有着相当大的差距。看起来，一个只有几十亿参数的语言模型似乎不可能在困难推理问题上取得与那些上千亿参数的模型相当的性能，难道复杂推理任务真的仅仅是大模型的游戏吗？

在我们这篇名为 CoRe 的工作中，我们证明了这并不是真的，即使是只有 6B 参数的语言模型，也可以在适当的引导下生成高质量的推理路径，同时这些优秀的例子可以被用作模型的进一步训练，达到更高的推理水平。我们的实验表明，像 GPT-J 这样大小的模型在数学推理任务上也可以与那些千亿参数的 LLMs 相媲美，甚至超过它们。

动机

CoT + LLMs 很强大，但是有什么地方可以改进呢？

1. 一个很明显的地方就是语言模型在推理的过程中没有监督和引导，我们都知道语言模型是从左到右地一路往下生成 token，这就导致了它有可能陷入一些逻辑不够严密的，质量较低的推理路径中，仅仅因为这些路径的 perplexity 更低。

2. 另一个方面是当语言模型生成多条推理路径时，这些路径之间是独立的，比如 Self-Consistency [6] 提出的采样多条再进行多数投票，而 OpenAI [7] 最早是使用训练了一个额外的 verifier 来挑选出多条 solutions 中最高分的那个作为答案，生成前面 reasoning paths 的经验并没有给接下来的生成带来更多的指导与经验，这很明显是一个不够 smart 与 efficient 的方法。

为了解决上述的两个问题，我们期望能够在语言模型生成推理路径的过程中引入监督与指导，借鉴人类思考的双系统理论，系统一是一种快思考，而系统二是一种慢思考，更适用于解决需要深思熟虑的问题，我们希望模仿这一种双系统互动的过程，将生成模型 generator 当作系统一，而验证模型 verifiers 当作系统二。

除此以外，对于模型每一次生成一条新的 solution，都能够得到一个反馈，从而给接下来的生成带来更好的路径选择。这种树状的搜索思路与蒙特卡洛树搜索（MCTS）的方法恰好十分吻合，我们便应用了这样的一个算法来控制整个推理过程，提出了一个名为 Cooperative Reasoning 的协同推理框架 CoRe。

我们训练了两个 verifiers 来给予 generator（语言模型）反馈，一个是 token-level verifier，另一个是 sentence-level verifier，这一做法是受 AlphaGo [8] 启发：

在下围棋时，AlphaGo 也使用了两个打分网络，一个在模型每走一步棋时就给出一个分数（对应我们的 token-level verifier），另一个会让模型通过 MCTS 在走完上一步后，把这盘棋下完，根据结果再给出一个分数（对应我们的 sentence-level verifier），很明显下围棋也是一个极其复杂的推理任务，为了使用语言模型解决数学推理问题，我们从 AlphaGo 的文章中获得了大量的启发。

3. 当解决了前两个问题后，我们希望能进一步提升语言模型的推理能力，因此我们使用上述提出的协同推理框架给训练集的 question 生成更多的 solutions，并且使用 generator 对它们的 perplexity 和 verifiers 对它们的分数进行过滤，得到了一批高质量的数据用于进一步 fine-tune，我们称这一过程为 Self-Thinking，同期工作 Self-Improve [9] 与我们不谋而合，但我们使用的模型要相对小得多。

CoRe

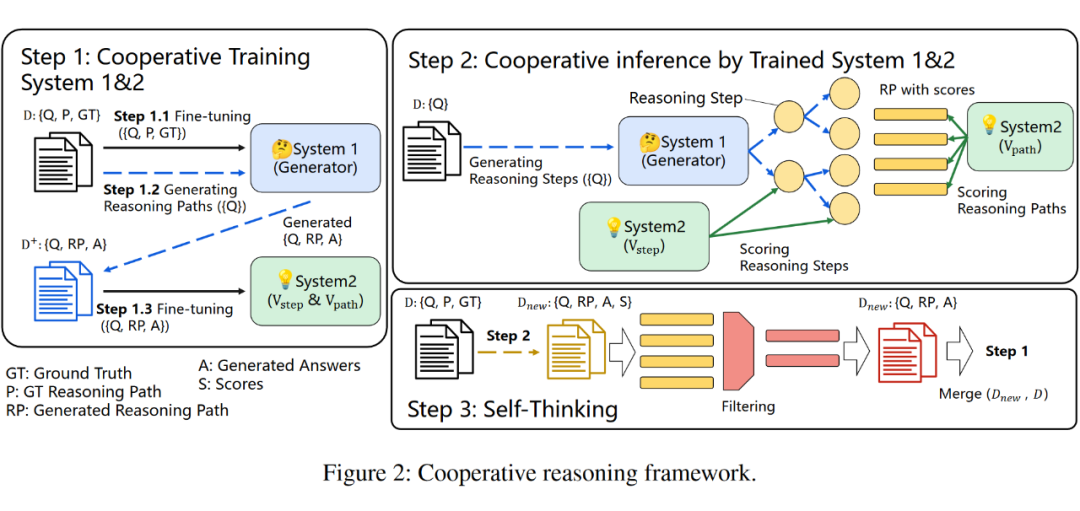
我们训练了一个 generator 与两个 verifier，generator 与 token-level verifier 都是一个 GPT-J，sentence-level verifier 我们采用了 DeBERTa，整体的方法框架如上图所示。在 Step 1，我们 follow 了 OpenAI [7] 的工作，在GSM8K fine-tune 得到了 generator 与两个 verifiers。

在 Step 2，不同于之前的工作是在完成所有的生成后再使用 verifier 来选择 solution，我们认为在生成的过程中间提供反馈非常重要，推理路径的搜索在指导下进行，那些高质量的路径会被更多地探索。我们使用了两个 verifiers，一个是 GPT-J 用于提供 token-level 的反馈，另一个用 DeBERTa 用于提供 sentence-level 反馈。我们利用 MCTS 算法将生成器和验证器结合起来，让它们共同解决推理问题。

在 Step 3，为了进一步提高模型的推理能力，我们利用这个协同推理框架来生成更多的例子以进一步微调语言模型和验证模型，形成了整套流程的闭环。值得注意一点是，我们发现直接用最终答案正确与否来过滤生成的例子效果并不理想。相反，我们通过生成器和验证器的合作来过滤它们，因而过滤其实也是一个协同过程，我们把这个过程称为自我思考（Self-Thinking）。最后，我们重复 Step 2 和 Step 3 直到性能饱和。

下图是推理过程的可视化：

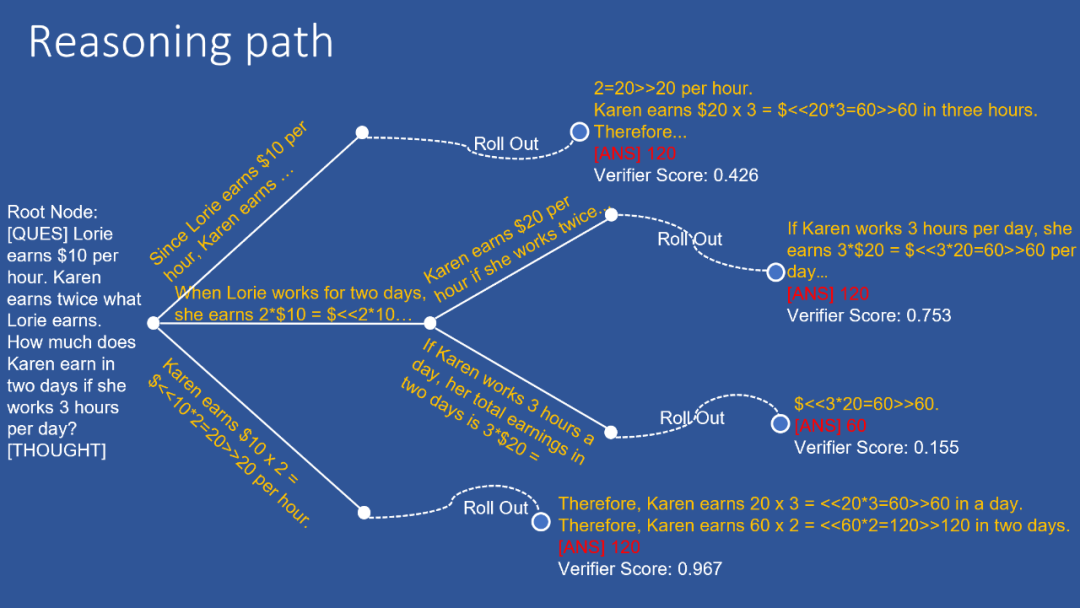
实验结果

我们在 GSM8K 上对模型进行了微调，而在其他数学推理数据集上进行的是 zero-shot。可以看出，推理能力可以在同一领域内转移，在 GSM8K 上的微调有助于语言模型解决其他数学推理问题。

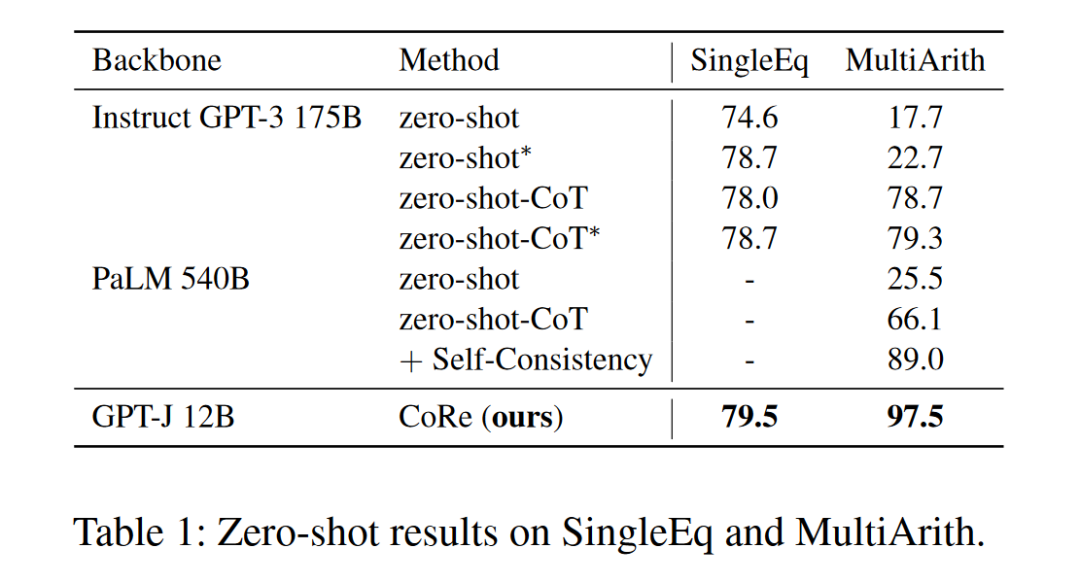
我们在其他数据集上的 zero-shot 结果超过了之前的 fine-tune SoTA。

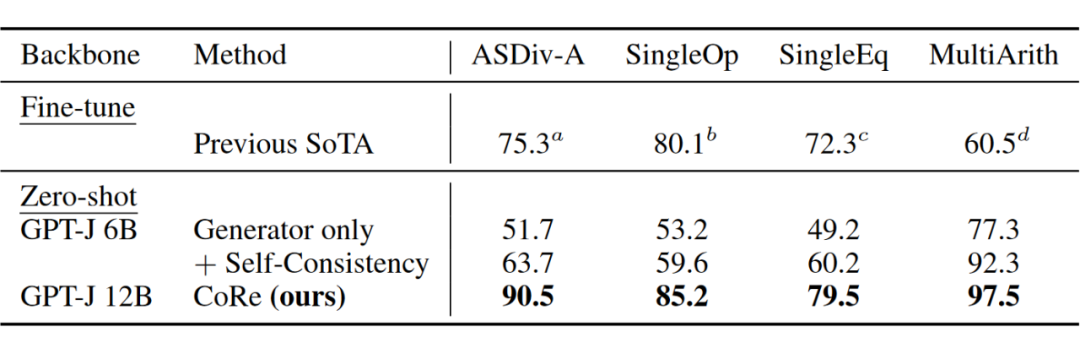
使用了 CoRe 的 GPT-J 可以与那些超大的语言模型相媲美。即使在最难的数据集 GSM8K 上，它也超过了 OpenAI 以前的微调 SoTA，后者使用两个 GPT-3 175B，一个作为生成器，一个作为验证器。

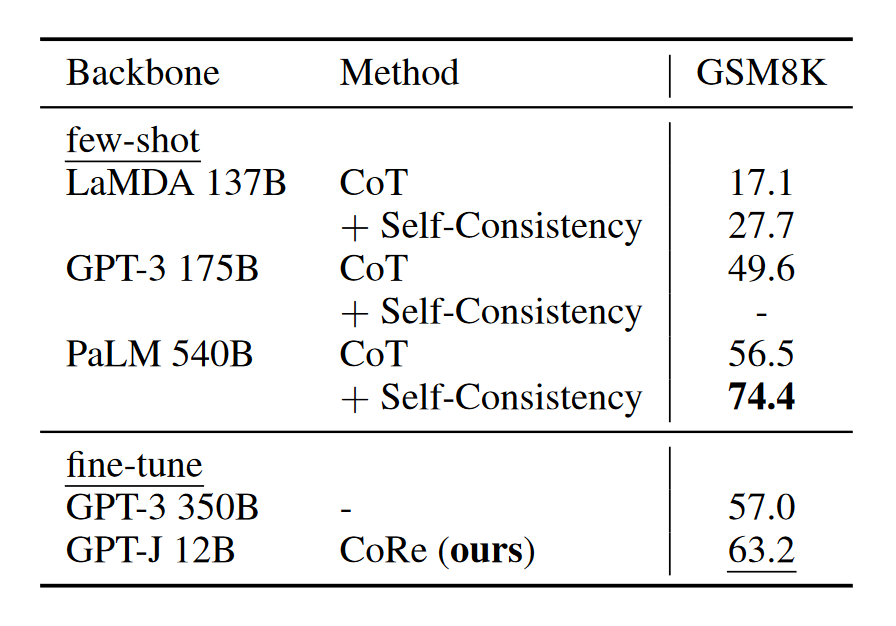
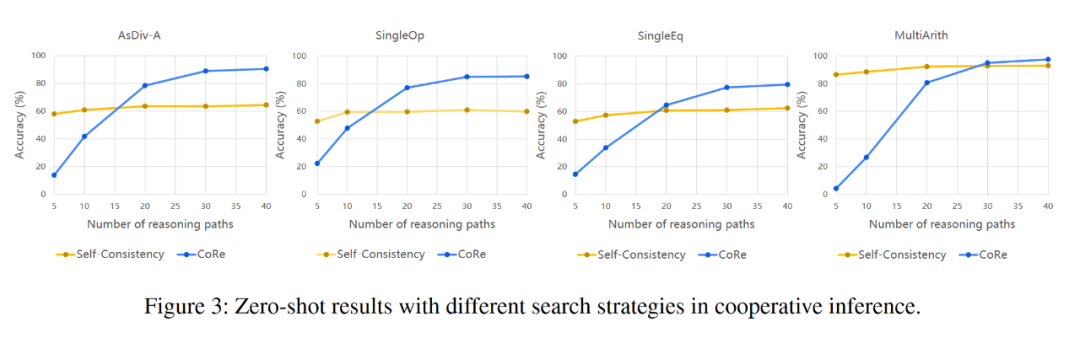
通过与 Self-Consistency 的对比可以看出，虽然我们的方法起于一个相对低的起点，但它增长的速率远远超过 Self-Consistency，且在超越其之后一直保持着更高的斜率，这意味着更慢的性能饱和速度，证明了这种带有引导的协同推理框架的有效性。

展望

虽然 LLMs 在各个方面展现出了很强大的性能，最近的研究也指出了它存在很严重的 hallucination 问题，它生成的内容并不是确定性的，采样时总会产生不确定性，因而有很多工作将 LLMs 与其他工具的结合，最容易想到的就是编程语言，事实上在 CoRe 发布在 arxiv 上的仅一个月内便出现了数篇这样的工作 [10] [11][12]。在未来 LLMs 很有可能接入各种各样的系统，作为一个总规划师，而非真正的执行者，比如近期的一些工作已经对这些有所探索 [13] [14] [15]。