小蓝本 第一本 《因式分解技巧》 第六章 二元二次式的分解 笔记(第六天)
- 前言
- 二元二次式的分解
- 研究对象
- 类型
- 普通二元二次式
- 基本形式
- 分解方法
- 总体总结——长十字相乘
- 注意
- 三元齐次式
- 基本形式
- 分解方法
- 总体总结——长十字相乘
- 注意
- 提示
- 习题6
- 题目
- 题解
前言
今天的干货是基于昨天的十字相乘来讲的,不知道十字相乘的,可以看一看我这篇博客十字相乘
二元二次式的分解
研究对象
普通二元二次式和三元齐次式
类型
普通二元二次式
基本形式
关于x和y的普通二元二次式 a x 2 + b x y + c y 2 + d x + e y + f ax^2+bxy+cy^2+dx+ey+f ax2+bxy+cy2+dx+ey+f
分解方法
- 将式子按基本形式理顺
- 把 a x 2 ax^2 ax2、 b x y bxy bxy、 c y 2 cy^2 cy2、 d x dx dx、 e y ey ey、 f f f 拆开看
- 先将
a
x
2
ax^2
ax2和
c
y
2
cy^2
cy2进行十字相乘凑
b
x
y
bxy
bxy,再将
c
y
2
cy^2
cy2系数拆开的2个因数和
f
f
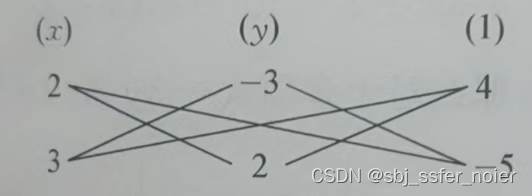
f进行十字相乘,如图:
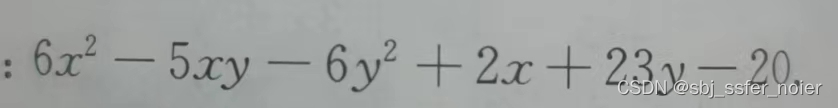
- 将 a x 2 ax^2 ax2和 f f f拆成的因数交叉相乘的和求出
- 若得到的和 = d =d =d,跳到6,否则跳到3
- 第一行3个数分别为 2 -3 4 写成 ( 2 x − 3 y + 4 ) (2x-3y+4) (2x−3y+4),第二行3个数分别为 3 2 -5 写成 ( 3 x + 2 y − 5 ) (3x+2y-5) (3x+2y−5)
- 拼起来得 ( 2 x − 3 y + 4 ) ( 3 x + 2 y − 5 ) (2x-3y+4)(3x+2y-5) (2x−3y+4)(3x+2y−5)
总体总结——长十字相乘
这就是为什么第五章的知识尤其重要,长十字相乘中用到2个普通二次三项式和1个二次齐次式
注意
建议再长十字相乘中将(x) (y) (1)标清楚
三元齐次式
基本形式
关于x、y、z 的三元齐次式 a x 2 + b x y + c y 2 + d x z + e y z + f z 2 ax^2+bxy+cy^2+dxz+eyz+fz^2 ax2+bxy+cy2+dxz+eyz+fz2
分解方法
- 将式子按基本形式理顺
- 把 a x 2 ax^2 ax2、 b x y bxy bxy、 c y 2 cy^2 cy2、 d x z dxz dxz、 e y z eyz eyz、 f z 2 fz^2 fz2 拆开看
- 先将
a
x
2
ax^2
ax2和
c
y
2
cy^2
cy2进行十字相乘凑
b
x
y
bxy
bxy,再将
c
y
2
cy^2
cy2系数拆开的2个因数和
f
z
2
fz^2
fz2进行十字相乘,如图:
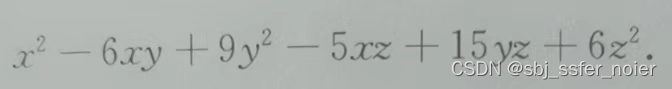
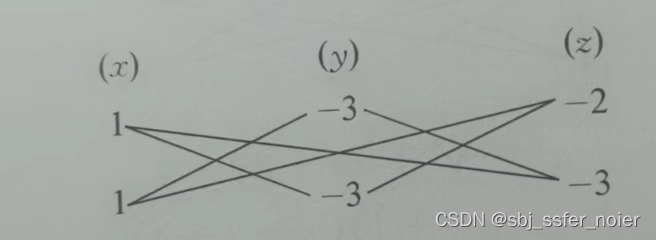
- 将 a x 2 ax^2 ax2和 f z 2 fz^2 fz2拆成的因数交叉相乘的和求出
- 若得到的和 = d =d =d,跳到6,否则跳到3
- 第一行3个数分别为 1 -3 -2 写成 ( x − 3 y − 2 z ) (x-3y-2z) (x−3y−2z),第二行3个数分别为 1 -3 -3 写成 ( x − 3 y − 3 z ) (x-3y-3z) (x−3y−3z)
- 拼起来得 ( x − 3 y − 2 z ) ( x − 3 y − 3 z ) (x-3y-2z)(x-3y-3z) (x−3y−2z)(x−3y−3z)
总体总结——长十字相乘
长十字相乘中用到3个二次齐次式
注意
将(x) (y) (z) 标清楚,别忘了z
提示
- 当某项系数为0(或不存在) 时,式子分解起来 更为简单。
- 普通二元二次式和三元齐次式不是一定能分解的
习题6
题目

题解

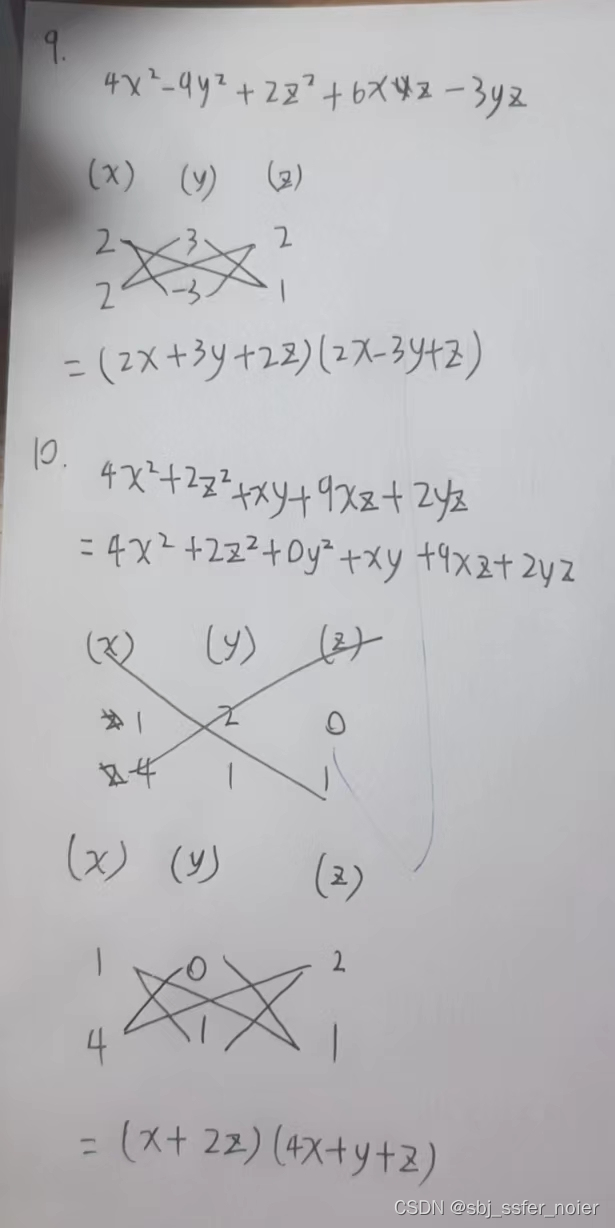


![[附源码]Python计算机毕业设计SSM基于的防疫隔离服务系统(程序+LW)](https://img-blog.csdnimg.cn/068cf872f7d942a4a4e6c72ffcd3041d.png)