强化学习算法
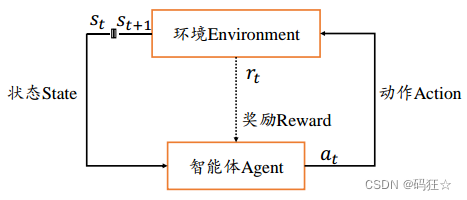
游戏模型如下:
策略网络输入状态s,输出动作a的概率分布如下: π ( a ∣ s ) \pi(a|s) π(a∣s)
多次训练轨迹如下
- r表示回报
- 横轴为T, 1个回合的步骤数
- 纵轴为N, 回合数,1行代表1条轨迹,符合概率分布P
[ s 11 a 11 r 11 … … s 1 t a 1 t r 1 t … … s 1 T a 1 T r 1 T … … … … … … s n 1 a n 1 r n 1 … … s n t a n t r n t … … s n T a n T r n T … … … … … … s N 1 a N 1 r N 1 … … s N t a N t r N t … … s N T a N T r N T ] \begin{bmatrix} s_{11} a_{11} r_{11} …… s_{1t} a_{1t} r_{1t} …… s_{1T} a_{1T} r_{1T}\\ …… …… ……\\ s_{n1} a_{n1} r_{n1} …… s_{nt} a_{nt} r_{nt}…… s_{nT} a_{nT} r_{nT} \\ …… …… ……\\ s_{N1} a_{N1} r_{N1} …… s_{Nt} a_{Nt} r_{Nt} …… s_{NT} a_{NT} r_{NT}\\ \end{bmatrix} s11a11r11……s1ta1tr1t……s1Ta1Tr1T………………sn1an1rn1……sntantrnt……snTanTrnT………………sN1aN1rN1……sNtaNtrNt……sNTaNTrNT
策略轨迹 τ = s 1 a 1 , s 2 a 2 , … … , s T a T \tau = s_{1} a_{1} , s_{2} a_{2},……,s_{T} a_{T} τ=s1a1,s2a2,……,sTaT
发生的概率
P
(
τ
)
=
P
(
s
1
a
1
,
s
2
a
2
,
…
…
,
s
T
a
T
)
P(\tau) = P(s_{1} a_{1} , s_{2} a_{2},……,s_{T} a_{T})
P(τ)=P(s1a1,s2a2,……,sTaT)
=
P
(
s
1
)
π
(
a
1
∣
s
1
)
P
(
s
2
∣
s
1
,
a
1
)
π
(
a
2
∣
s
2
)
P
(
s
3
∣
s
1
,
a
1
,
s
2
,
a
2
)
…
…
= P(s_{1})\pi(a_{1}|s_{1})P(s_{2}|s_{1},a_{1})\pi(a_{2}|s_{2})P(s_{3}|s_{1},a_{1},s_{2},a_{2})……
=P(s1)π(a1∣s1)P(s2∣s1,a1)π(a2∣s2)P(s3∣s1,a1,s2,a2)……
=
P
(
s
1
)
∏
t
=
1
T
−
1
π
(
a
t
∣
s
t
)
P
(
s
t
+
1
∣
s
1
,
a
1
,
.
.
.
.
.
.
,
s
t
,
a
t
)
= P(s_{1})\prod_{t=1}^{T-1}\pi(a_{t}|s_{t})P(s_{t+1}|s_{1},a_{1},......,s_{t},a_{t})
=P(s1)t=1∏T−1π(at∣st)P(st+1∣s1,a1,......,st,at)
根据 马尔科夫性(Markov Property),简化为:
P
(
τ
)
=
P
(
s
1
)
∏
t
=
1
T
−
1
π
(
a
t
∣
s
t
)
P
(
s
t
+
1
∣
s
t
,
a
t
)
P(\tau) = P(s_{1})\prod_{t=1}^{T-1}\pi(a_{t}|s_{t})P(s_{t+1}|s_{t},a_{t})
P(τ)=P(s1)t=1∏T−1π(at∣st)P(st+1∣st,at)
奖励
在每次智能体与环境的交互过程中,均会得到一个滞后的奖励
r
t
=
r
(
s
t
,
a
t
)
r_{t} = r(s_{t},a_{t})
rt=r(st,at)
一次交互轨迹𝜏的累积奖励:
R
τ
=
∑
t
=
1
T
−
1
r
t
R_{\tau } = \sum_{t=1}^{T-1} r_{t}
Rτ=t=1∑T−1rt
其中𝑇为轨迹的步数。 如果只考虑从轨迹的中间状态𝑠𝑡开始𝑠𝑡, 𝑠𝑡+1, . . . , 𝑠𝑇的累积奖励:
R
(
s
t
)
=
∑
k
=
1
T
−
t
−
1
r
t
+
k
R(s_{t}) = \sum_{k=1}^{T-t-1} r_{t+k}
R(st)=k=1∑T−t−1rt+k
为了权衡近期奖励与长期奖励的重要性, 更多地使用随着时间衰减的折扣奖励:
R
τ
=
∑
t
=
1
T
−
1
γ
t
−
1
r
t
R_{\tau } = \sum_{t=1}^{T-1} \gamma ^{t-1} r_{t}
Rτ=t=1∑T−1γt−1rt
其中𝛾 ∈ [0,1]叫做折扣率.
我们希望找到一个策略𝜋(𝑎|𝑠)模型,使得在策略𝜋(𝑎|𝑠)控制下的智能体与环境交互产
生的轨迹𝜏的总奖励𝑅(𝜏)越高越好。由于环境状态转移和策略都具有随机性, 同样的策略模
型作用于同初始状态的同一环境,也可能产生截然不同的轨迹序列𝜏。 因此,强化学习的目
标是最大化期望奖励(Expected Return):
J
(
π
(
θ
)
)
=
E
τ
∼
P
(
τ
)
[
R
(
τ
)
]
=
E
τ
∼
P
(
τ
)
[
∑
t
=
1
T
−
1
γ
t
−
1
r
t
]
J(\pi (\theta )) = E_{\tau \sim P(\tau) } \left [ R(\tau) \right ] = E_{\tau \sim P(\tau) }\left [ \sum_{t=1}^{T-1} \gamma ^{t-1} r_{t} \right ]
J(π(θ))=Eτ∼P(τ)[R(τ)]=Eτ∼P(τ)[t=1∑T−1γt−1rt]
把期望写成求和平均形式:
J
(
π
(
θ
)
)
=
1
N
∑
n
=
1
N
(
P
(
τ
n
)
R
(
τ
n
)
)
,其中
τ
n
表示第
n
条轨迹
J(\pi (\theta )) =\frac{1}{N}\sum_{n=1}^{N} \left ( P(\tau ^{n}) R\left ( \tau ^{n} \right ) \right ) ,其中 \tau ^{n} 表示 第n条轨迹
J(π(θ))=N1n=1∑N(P(τn)R(τn)),其中τn表示第n条轨迹
训练的目标是寻找一组参数𝜃代表的策略网络𝜋𝜃,使得𝐽(𝜋𝜃)最大:
θ
∗
=
a
r
g
m
a
x
θ
E
τ
∼
P
(
τ
)
[
R
(
τ
)
]
\theta ^{*} = \underset{\theta }{argmax} E_{\tau \sim P(\tau) } \left [ R(\tau) \right ]
θ∗=θargmaxEτ∼P(τ)[R(τ)]
其中𝑝(𝜏)代表了轨迹𝜏的分布, 它由状态转移概率𝑝(𝑠′|𝑠, 𝑎)和策略𝜋(𝑎|𝑠)共同决定。 策略𝜋
的好坏可以通过𝐽(𝜋𝜃)衡量,期望奖励越大,策略越优良; 反之则策略越差。
梯度更新
∂ J ∂ θ = 1 N ∑ n = 1 N ∂ ∂ θ ( ( P ( s 1 ) ∏ t = 1 T − 1 π ( a t ∣ s t ) P ( s t + 1 ∣ s t , a t ) ) R ( n ) ) \frac{\partial J}{\partial \theta } = \frac{1}{N}\sum_{n=1}^{N} \frac{\partial}{\partial \theta } \left ( \left ( P(s_{1})\prod_{t=1}^{T-1}\pi(a_{t}|s_{t})P(s_{t+1}|s_{t},a_{t}) \right ) R(n) \ \right ) ∂θ∂J=N1n=1∑N∂θ∂((P(s1)t=1∏T−1π(at∣st)P(st+1∣st,at))R(n) )
考虑
d
log
f
(
x
)
d
x
=
1
f
(
x
)
d
f
(
x
)
d
x
\frac{d\log_{}{f(x)} }{dx} = \frac{1}{f(x)} \frac{df(x)}{dx}
dxdlogf(x)=f(x)1dxdf(x)
将log ∏∙转换为∑ log(∙)形式
∂
J
∂
θ
=
1
N
∑
n
=
1
N
R
(
n
)
∂
∂
θ
(
log
p
(
s
1
)
+
∑
t
=
1
T
−
1
log
π
θ
(
a
t
∣
s
t
)
+
log
p
(
s
t
+
1
∣
s
t
,
a
t
)
)
\frac{\partial J}{\partial \theta } = \frac{1}{N}\sum_{n=1}^{N} R(n) \frac{\partial}{\partial\theta }\left ( \log_{}{p(s_{1}) } +\sum_{t=1}^{T-1} \log_{}{\pi _{\theta } (a_{t}| s_{t} )} + \log_{}{p(s_{t+1}|s_{t},a_{t})} \right )
∂θ∂J=N1n=1∑NR(n)∂θ∂(logp(s1)+t=1∑T−1logπθ(at∣st)+logp(st+1∣st,at))
第n条轨迹分布𝑝(n)与𝜃 无关,奖励R(n)与𝜃 无关,看成常数:
∂
J
∂
θ
=
1
N
∑
n
=
1
N
R
(
n
)
(
∑
t
=
1
T
−
1
∂
∂
θ
log
π
θ
(
a
t
∣
s
t
)
)
\frac{\partial J}{\partial \theta } = \frac{1}{N}\sum_{n=1}^{N}R(n) \left ( \sum_{t=1}^{T-1} \frac{\partial}{\partial\theta }\log_{}{\pi _{\theta } (a_{t}| s_{t} )} \right )
∂θ∂J=N1n=1∑NR(n)(t=1∑T−1∂θ∂logπθ(at∣st))
写成期望形式:
∂ J ∂ θ = E τ ∼ P ( τ ) [ ( ∑ t = 1 T − 1 ∂ ∂ θ log π θ ( a t ∣ s t ) ) R ( τ ) ] \frac{\partial J}{\partial \theta } = \ E_{\tau \sim P(\tau) }\left [ \left ( \sum_{t=1}^{T-1} \frac{\partial}{\partial\theta }\log_{}{\pi _{\theta } (a_{t}| s_{t} )} \right ) R(\tau)\right ] ∂θ∂J= Eτ∼P(τ)[(t=1∑T−1∂θ∂logπθ(at∣st))R(τ)]
有了上述的表达式后,我们就可以通过 TensorFlow 的自动微分工具方便地求解出𝐽(𝜋𝜃)的最大值
最后利用梯度上升算法更新即可
强化学习算法(REINFORCE 算法)
start : 随机初始化参数𝜽
for :
根据策略𝝅𝜽(𝒂𝒕|𝒔𝒕)与环境交互, 生成多条轨迹{𝝉(𝒏)}
计算𝑹(𝝉(𝒏))
计算𝝏𝑱(𝜽)
更新网络参数𝜽′ ← 𝜽 + 𝜼 ∙ 𝝏𝑱(𝜽)
end : 训练回合数达到要求
out : 策略网络𝝅𝜽(𝒂𝒕|𝒔𝒕)