题目来源：https://leetcode.cn/problems/combination-sum-iv/description/

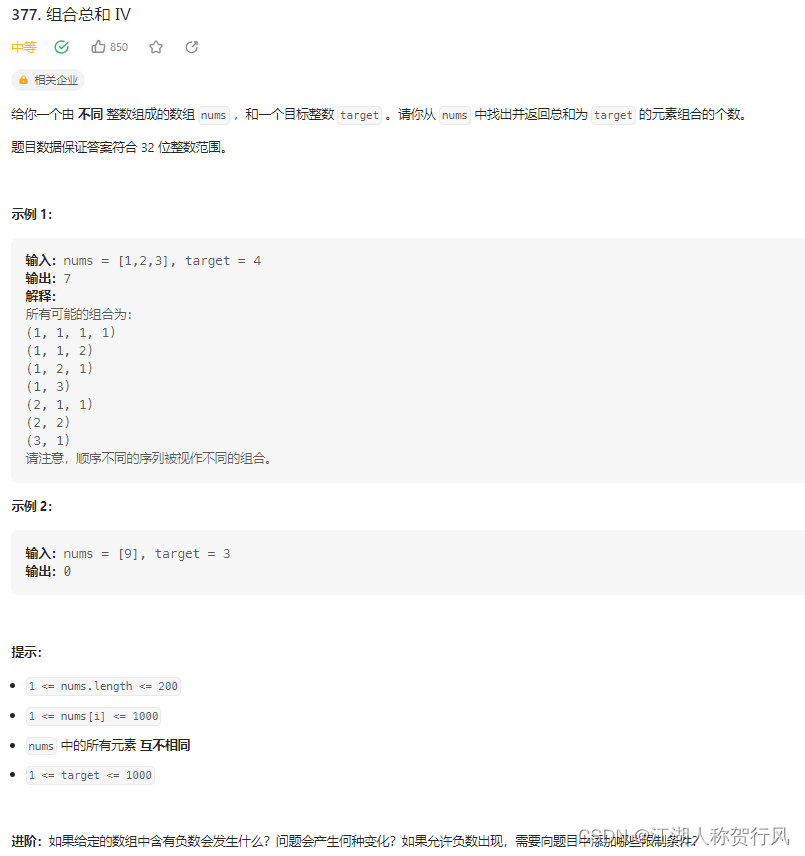
C++题解（来源代码随想录）： 本题求的是排列总和，而且仅仅是求排列总和的个数，并不是把所有的排列都列出来。动规五部曲分析如下：

1. 确定dp数组以及下标的含义。dp[i]: 凑成目标正整数为i的排列个数为dp[i]
2. 确定递推公式。dp[i]（考虑nums[j]）可以由 dp[i - nums[j]]（不考虑nums[j]） 推导出来。递推公式是dp[i] += dp[i - nums[j]];
3. dp数组如何初始化。因为递推公式dp[i] += dp[i - nums[j]]的缘故，dp[0]要初始化为1，这样递归其他dp[i]的时候才会有数值基础。
4. 确定遍历顺序。个数可以不限使用，说明这是一个完全背包。得到的集合是排列，说明需要考虑元素之间的顺序。如果求组合数就是外层for循环遍历物品，内层for遍历背包。如果求排列数就是外层for遍历背包，内层for循环遍历物品。如果把遍历nums（物品）放在外循环，遍历target的作为内循环的话，举一个例子：计算dp[4]的时候，结果集只有 {1,3} 这样的集合，不会有{3,1}这样的集合，因为nums遍历放在外层，3只能出现在1后面！所以本题遍历顺序最终遍历顺序：target（背包）放在外循环，将nums（物品）放在内循环，内循环从前到后遍历。
5. 举例来推导dp数组

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<int> dp(target + 1, 0);
        dp[0] = 1;
        for (int i = 0; i <= target; i++) { // 遍历背包
            for (int j = 0; j < nums.size(); j++) { // 遍历物品
                if (i - nums[j] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]]) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
};