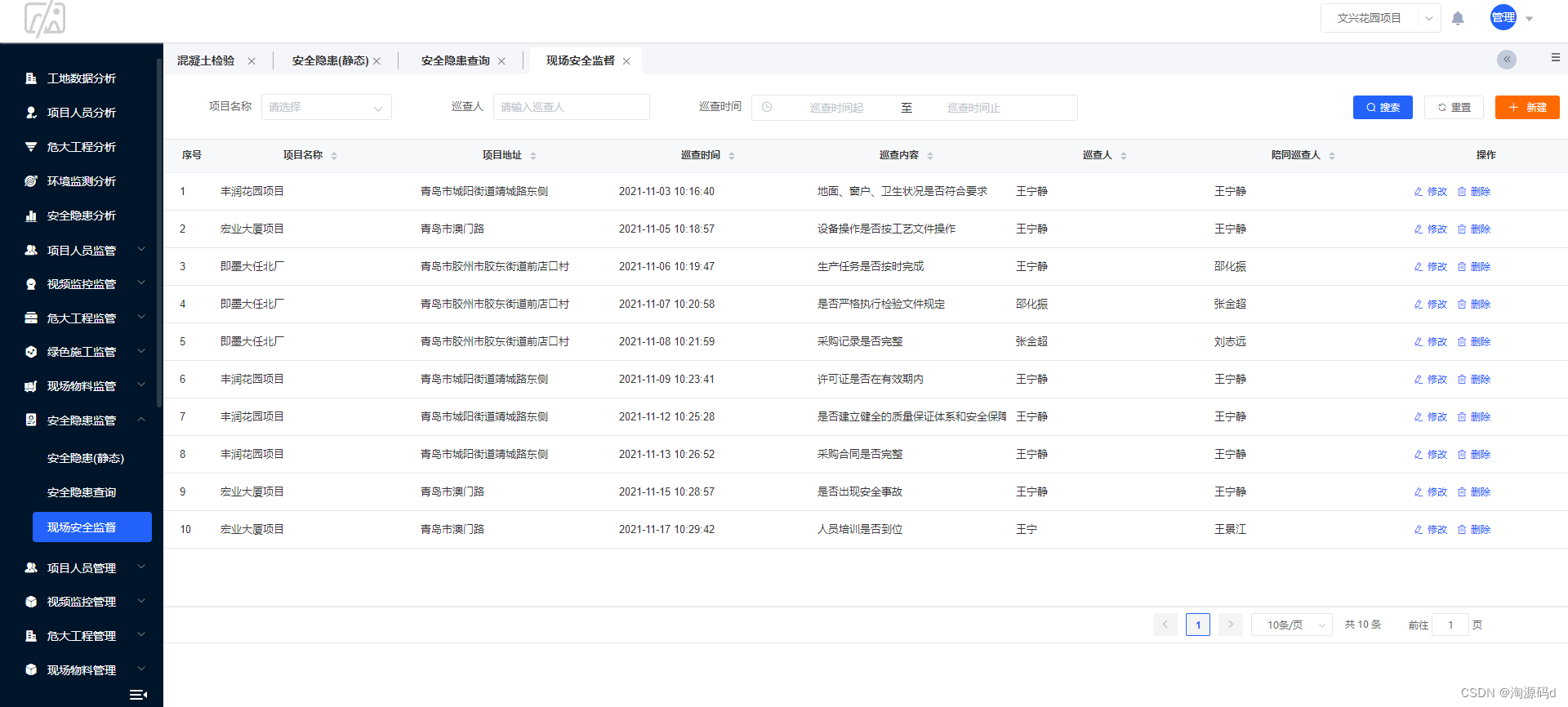
有一个环形的公路,上面共有n站,现在给定了顺时针第i站到第i+1站之间的距离(特殊的,也给出了第n站到第1站的距离),小*想着沿着公路第x站走到第y站,她想知道最短的距离是多少?
输入描述:
第一行输入一个正整数n,代表站的数量。第二行输入n个正整数ai,前 n-1个数代表顺时针沿看公路走,i站到第i+1站之间的距离:最后一个正整数代表顺时针沿着公路走,第n站到第1 站的距离
第三行输入两个正整数x和y,代表小美的出发地和目的地。
1 <=n <=10^5
1<=ai < 10^9
1<=x,y<=n
输入:
3
1 2 2
2 3
输出:
2
大厂的笔试永远这么晦涩难懂?刚看到题的时候只能知道它是一道图论问题,题目描述的确实有一点绕,现在让我们来分析一波题的含义:
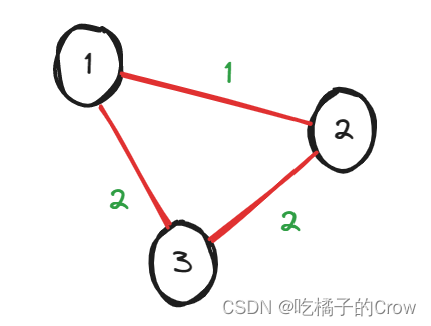
假如你现在在车站1,假如你的目的地是车站3,你选择哪条路路径最短?毫无疑问肯定是由车站1直接到车站3路径是最短的,我们可以用眼睛直接观察出来,可是计算机可不能直接得出正确答案?如果你做图论的相关题较多的话,其实你刚看到这道题,心里便会想到这道题,和这题类似的leetcode原题(K 站中转内最便宜的航班),我们今天以讲解leetcode为例,这道题知识稍微在那道题中做了变形就出来了
有
n个城市通过一些航班连接。给你一个数组flights,其中flights[i] = [fromi, toi, pricei],表示该航班都从城市fromi开始,以价格pricei抵达toi。现在给定所有的城市和航班,以及出发城市
src和目的地dst,你的任务是找到出一条最多经过k站中转的路线,使得从src到dst的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出-1。n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]] src = 0, dst = 2, k = 1 输出: 200 解释: 城市航班图如下:


其实K站中转内最便宜的航班其实约束条件更多一点,其要找到一条最多经过k站中转的路线
我们这次使用递归来解决这个问题

由于题目中给出我们这些信息,所以我们就可以根据这些信息去构建邻接表:

因为我们函数在递归的时候,函数中的参数是我们的起点位置,所以我们因为构造一个to-[from,price]的邻接矩阵
//邻接表的数据结构
Map<Integer,List<Integer[]>> map=new HashMap<>();
//遍历每一个数组,取出对应的元素
for(int[] f:flights){
//起点
int from=f[0];
//终点
int to=f[1];
//两点之间的距离
int price=f[2];
//如果不包含
if(!map.containsKey(to)){
map.put(to,new LinkedList<>());
}
//构建邻接表
map.get(to).add(new Integer[]{from,price});
}接下来就是我们寻找起点和终点的最短路径的最短距离
函数标签:
//dst指的是当前点 k指的是剩下可以步数
private int dfs(int dst, int k) {}如果我们的起点正好等于我们的终点,直接返回0(说明已经找到了一条可以到达目的地的路线)
if(dst==src){
return 0;
}如果k==0,说明当前已经不满足题目的要求(没到终点且步数为0),直接返回-1
if(k==0){
return -1;
}如果当前节点合法,那么就遍历与它直接相邻的节点
if(map.containsKey(dst)){
//遍历邻接表
for(Integer[] v:map.get(dst)){
//起点
int from=v[0];
//所需要的花费
int price=v[1];
//递归下一个节点
int sub=dfs(from,k-1);
//如果sub不是-1,就说明该路线是合法的
if(sub!=-1){
//当前节点距离终点的路径=下一个节点距离终点的路径+当前节点距离下一个节点的距离
res=Math.min(res,sub+price);
}
}
return res;
}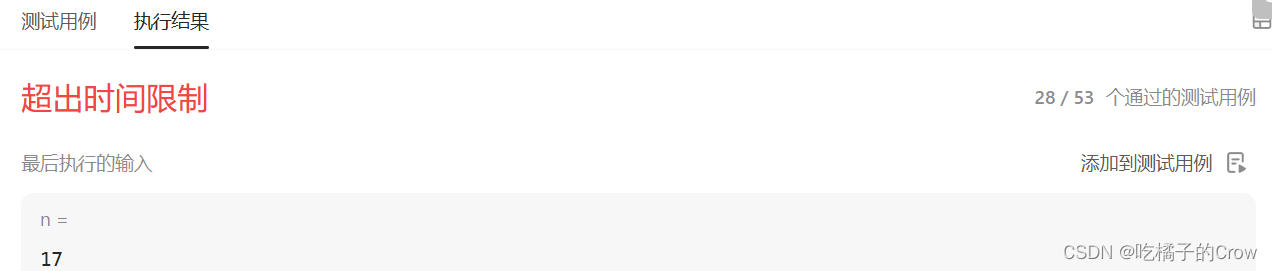
这种递归的方法肯定是超时,所以我们使用记忆化搜索的方式去进行优化
int[][]memo;
memo=new int[n][k+1];//如果曾经已经计算过,直接返回答案
if(memo[dst][k]!=-88)return memo[dst][k]; res= res==Integer.MAX_VALUE?-1:res;
memo[dst][k]=res;
动态规划方式就先不做介绍了,大家下去可以自行试一试
源码如下:
Map<Integer,List<Integer[]>> map=new HashMap<>();
//记忆化数组
int[][]memo;
//起点
int src;
//终点
int dst;
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
this.dst=dst;
this.src=src;
//k表示的节点,我们将结点转换成步数,更利于计算
k++;
memo=new int[n][k+1];
//对记忆化数组进行初始化
for(int[] row:memo){
Arrays.fill(row,-88);
}
//构造邻接表
for(int[] f:flights){
int from=f[0];
int to=f[1];
int price=f[2];
if(!map.containsKey(to)){
map.put(to,new LinkedList<>());
}
map.get(to).add(new Integer[]{from,price});
}
return dfs(dst,k);
}
//表示从dst的走k步的最小价格
private int dfs(int dst, int k) {
if(dst==src){
return 0;
}
if(k==0){
return -1;
}
if(memo[dst][k]!=-88)return memo[dst][k];
int res=Integer.MAX_VALUE;
if(map.containsKey(dst)){
for(Integer[] v:map.get(dst)){
int from=v[0];
int price=v[1];
int sub=dfs(from,k-1);
if(sub!=-1){
res=Math.min(res,sub+price);
}
}
}
res= res==Integer.MAX_VALUE?-1:res;
memo[dst][k]=res;
return memo[dst][k];
}我们再来看这道所谓大厂的笔试题:这道题过程跟这个题一模一样,我们只需要将上面这个题中的k这个约束给省略掉,这道题也就出来了
代码如下:
Map<Integer,List<Integer[]>> map=new HashMap<>();
int[]memo;
int src;
int dst;
public int findCheapestPrice(int n, int[][] flights, int src, int dst) {
this.dst=dst;
this.src=src;
memo=new int[n];
Arrays.fill(memo,-88);
for(int[] f:flights){
int from=f[0];
int to=f[1];
int price=f[2];
if(!map.containsKey(to)){
map.put(to,new LinkedList<>());
}
map.get(to).add(new Integer[]{from,price});
}
return dfs(dst);
}
private int dfs(int dst) {
if(dst==src){
return 0;
}
if(memo[dst]!=-88)return memo[dst];
int res=Integer.MAX_VALUE;
if(map.containsKey(dst)){
for(Integer[] v:map.get(dst)){
int from=v[0];
int price=v[1];
int sub=dfs(from);
if(sub!=-1){
res=Math.min(res,sub+price);
}
}
}
res= res==Integer.MAX_VALUE?-1:res;
memo[dst]=res;
return memo[dst];
}
知识ACM模式下我们的所有参数都需要我们手动的去输入,这点也是比较关键点的因素:
起先我是这样写的:
Scanner scanner=new Scanner(System.in);
int n=scanner.nextInt();
int[][] nums=new int[n][3];
int index=0;
//遍历每个数组
for(int[] num:nums){
while(scanner.hasNextInt()){
//给每个数组进行赋值
for(int i=0;i<num.length;i++) {
if(i==n-1){
num[0]=i;
num[1]=0;
num[2]=scanner.nextInt();
}else{
num[0]=i;
num[1]=i+1;
num[2]=scanner.nextInt();
}
}
break;
}
}
int start=scanner.nextInt();
int end=scanner.nextInt();最后半天一直在死循环,后来发现,每个数组就3个元素,我这个for循环加的位置明显就有问题,所以一直在死循环,所以果断换了一种方式,及时止损
Scanner scanner = new Scanner(System.in);
System.out.print("输入行数:");
int n = scanner.nextInt();
int m = 3;
int[][] nums = new int[n][m];
System.out.println("输入二维数组中的值:");
//利用双层for循环进行定点输入
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
nums[i][j] = scanner.nextInt();
}
}
System.out.println("输入的二维数组为:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
System.out.print(nums[i][j] + " ");
}
System.out.println();
}
int start = scanner.nextInt();
int end = scanner.nextInt();我们将测试案例试一试:

这样很明显示我们手动的输入了数组中的元素,这样很显然是不符合题意的,那么我们这么样输入[1 2 2] 会自动生成[[0,1,1],[1,2,2],[2,0,3]]这个数组呢?我们先来说明它这个数组是是怎么生成的?

因为我们的数组是从0开始计数的,所以我们应该写成这样

我们开始ACM输入:
System.out.println("输入二维数组中的值:");
//输入一行时ACM输入
while(scanner.hasNextInt()){
for(int i=0;i<n;i++){
int dist=scanner.nextInt();
//如果是最后一个直接指向第一个节点
if(i==n-1){
int[] num=nums[i];
num[0]=i;
num[1]=0;
num[2]=dist;
//不是第一个直接指向后一个节点
}else{
int[] num=nums[i];
num[0]=i;
num[1]=i+1;
num[2]=dist;
}
}
//这个break记得加,要不就会死循环
break;
}
System.out.println("输入的二维数组为:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
System.out.print(nums[i][j] + " ");
}
System.out.println();
}

最后我们这道题也就讲解完了,ACM输入的时候对于很多笔试经验少的同学确实是一个挑战,希望大家刷题的过程中多使用ACM刷题,leetcode的话尽量脱离有提示的工具,最好在网页上进行写
ACM源代码输入:
Scanner scanner = new Scanner(System.in);
System.out.print("输入行数:");
int n = scanner.nextInt();
int m = 3;
int[][] nums = new int[n][m];
System.out.println("输入二维数组中的值:");
while(scanner.hasNextInt()){
for(int i=0;i<n;i++){
int dist=scanner.nextInt();
if(i==n-1){
int[] num=nums[i];
num[0]=i;
num[1]=0;
num[2]=dist;
}else{
int[] num=nums[i];
num[0]=i;
num[1]=i+1;
num[2]=dist;
}
}
break;
}
System.out.println("输入的二维数组为:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
System.out.print(nums[i][j] + " ");
}
System.out.println();
}
int start = scanner.nextInt();
//输入的是起点为1,数组的起点为0,所以需要减1
start=start-1;
int end = scanner.nextInt();
end=end-1;如果有更高的ACM输入的方式或者是解题更妙的技巧,欢迎大家来评论区进行评论!!!