代码随想录算法训练营第55天｜动态规划part12｜309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费、总结

news2024/12/30 3:37:47

代码随想录算法训练营第55天｜动态规划part12｜309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费、总结

309.最佳买卖股票时机含冷冻期

思路：

区别在第i天持有股票的当天买入的情况，买入因为有冷静期1天，如果之前有过交易，手里的利润应该是dp[i-1-1][1]也就是前两天不持有股票情况下的最大利润，然后再当天买入，就是dp[i-1-1][1]-price[i]

其他的地方都一样。

代码：

python

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        '''
        状态有几种：
        第i天持有股票：1. 继续持有 2. 买入 
        dp[i][0] = max(dp[i-1][0], dp[i-1-1][1]-price[i])
        第i天不持有股票：1. 当天卖出，后一天不允许交易 2. 前一天卖出今天是冷静期
        dp[i][1] = max(dp[i-1][0] + price[i], dp[i-1][1])
        
        '''
        dp = [[0, 0] for _ in range(len(prices))]

        dp[0][0] = 0 - prices[0]
        dp[0][1] = 0

        for i in range(1, len(prices)):
            if i > 1: 
                dp[i][0] = max(dp[i-1][0], dp[i-1-1][1]-prices[i])
            else:
                dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i])

            dp[i][1] = max(dp[i-1][1], prices[i] + dp[i-1][0])

        return dp[len(prices)-1][1]

代码随想录

这道题的重点在于全面的分析出有几种状态！！！

思路：

相对于动态规划：122.买卖股票的最佳时机II (opens new window)，本题加上了一个冷冻期

动规五部曲，分析如下：

确定dp数组以及下标的含义

dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]。

其实本题很多同学搞的比较懵，是因为出现冷冻期之后，状态其实是比较复杂度，例如今天买入股票、今天卖出股票、今天是冷冻期，都是不能操作股票的。

具体可以区分出如下四个状态：

状态一：持有股票状态（当天持有，和 一直持有）
不持有股票状态，这里就有两种卖出股票状态
- 状态二：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）
- 状态三：今天卖出股票
状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

j的状态为：

0：状态一
1：状态二
2：状态三
3：状态四

很多题解为什么讲的比较模糊，是因为把这四个状态合并成三个状态了，其实就是把状态二和状态四合并在一起了。

从代码上来看确实可以合并，但从逻辑上分析合并之后就很难理解了，所以我下面的讲解是按照这四个状态来的，把每一个状态分析清楚。

如果大家按照代码随想录顺序来刷的话，会发现买卖股票最佳时机 1，2，3，4 的题目讲解中

动态规划：121.买卖股票的最佳时机(opens new window)
动态规划：122.买卖股票的最佳时机II(opens new window)
动态规划：123.买卖股票的最佳时机III(opens new window)
动态规划：188.买卖股票的最佳时机IV(opens new window)

「今天卖出股票」我是没有单独列出一个状态的归类为「不持有股票的状态」，而本题为什么要单独列出「今天卖出股票」一个状态呢？

因为本题我们有冷冻期，而冷冻期的前一天，只能是「今天卖出股票」状态，如果是「不持有股票状态」那么就很模糊，因为不一定是卖出股票的操作。

注意这里的每一个状态，例如状态一，是持有股票股票状态并不是说今天一定就买入股票，而是说保持买入股票的状态即：可能是前几天买入的，之后一直没操作，所以保持买入股票的状态。

确定递推公式

达到买入股票状态（状态一）即：dp[i][0]，有两个具体操作：

操作一：前一天就是持有股票状态（状态一），dp[i][0] = dp[i - 1][0]
操作二：今天买入了，有两种情况
- 前一天是冷冻期（状态四），dp[i - 1][3] - prices[i]
- 前一天是保持卖出股票的状态（状态二），dp[i - 1][1] - prices[i]

那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);

达到保持卖出股票状态（状态二）即：dp[i][1]，有两个具体操作：

操作一：前一天就是状态二
操作二：前一天是冷冻期（状态四）

dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);

达到今天就卖出股票状态（状态三），即：dp[i][2] ，只有一个操作：

昨天一定是持有股票状态（状态一），今天卖出

即：dp[i][2] = dp[i - 1][0] + prices[i];

达到冷冻期状态（状态四），即：dp[i][3]，只有一个操作：

昨天卖出了股票（状态三）

dp[i][3] = dp[i - 1][2];

综上分析，递推代码如下：

dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];

dp数组如何初始化

如果是持有股票状态（状态一）那么：dp[0][0] = -prices[0]，一定是当天买入股票。

保持卖出股票状态（状态二），这里其实从「状态二」的定义来说，很难明确应该初始多少，这种情况我们就看递推公式需要我们给他初始成什么数值。

如果i为1，第1天买入股票，那么递归公式中需要计算 dp[i - 1][1] - prices[i] ，即 dp[0][1] - prices[1]，那么大家感受一下 dp[0][1] （即第0天的状态二）应该初始成多少，只能初始为0。想一想如果初始为其他数值，是我们第1天买入股票后手里还剩的现金数量是不是就不对了。

今天卖出了股票（状态三），同上分析，dp[0][2]初始化为0，dp[0][3]也初始为0。

确定遍历顺序

从递归公式上可以看出，dp[i] 依赖于 dp[i-1]，所以是从前向后遍历。

举例推导dp数组

以 [1,2,3,0,2] 为例，dp数组如下：

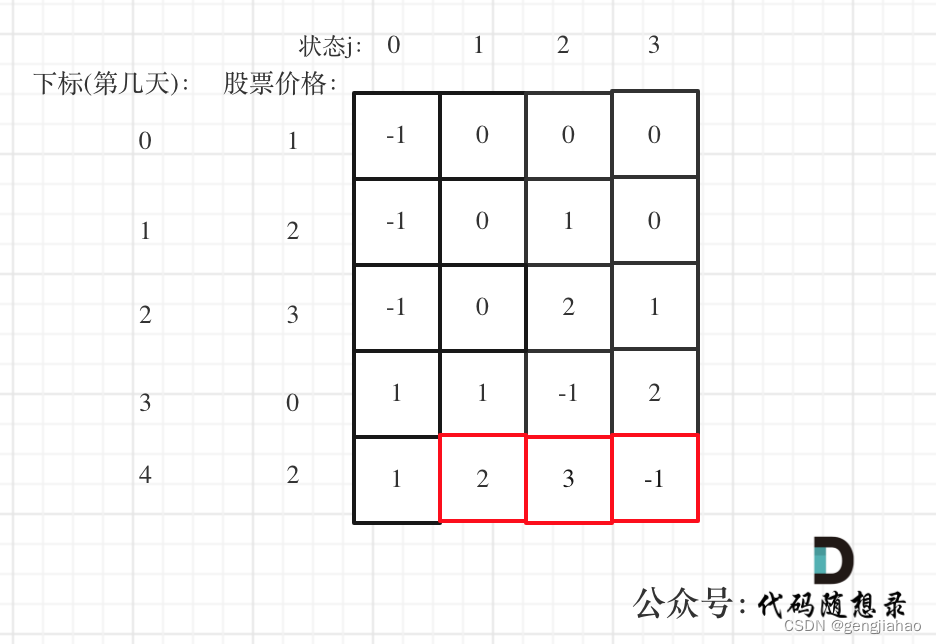
在这里插入图片描述
最后结果是取状态二，状态三，和状态四的最大值，不少同学会把状态四忘了，状态四是冷冻期，最后一天如果是冷冻期也可能是最大值。

代码：

python

from typing import List

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        if n == 0:
            return 0
        dp = [[0] * 4 for _ in range(n)]  # 创建动态规划数组，4个状态分别表示持有股票、不持有股票且处于冷冻期、不持有股票且不处于冷冻期、不持有股票且当天卖出后处于冷冻期
        dp[0][0] = -prices[0]  # 初始状态：第一天持有股票的最大利润为买入股票的价格
        for i in range(1, n):
            dp[i][0] = max(dp[i-1][0], max(dp[i-1][3], dp[i-1][1]) - prices[i])  # 当前持有股票的最大利润等于前一天持有股票的最大利润或者前一天不持有股票且不处于冷冻期的最大利润减去当前股票的价格
            dp[i][1] = max(dp[i-1][1], dp[i-1][3])  # 当前不持有股票且处于冷冻期的最大利润等于前一天持有股票的最大利润加上当前股票的价格
            dp[i][2] = dp[i-1][0] + prices[i]  # 当前不持有股票且不处于冷冻期的最大利润等于前一天不持有股票的最大利润或者前一天处于冷冻期的最大利润
            dp[i][3] = dp[i-1][2]  # 当前不持有股票且当天卖出后处于冷冻期的最大利润等于前一天不持有股票且不处于冷冻期的最大利润
        return max(dp[n-1][3], dp[n-1][1], dp[n-1][2])  # 返回最后一天不持有股票的最大利润

714. 买卖股票的最佳时机含手续费

思路：

相对122.买卖股票的最佳时机II ，本题只需要在计算卖出操作的时候减去手续费就可以了，代码几乎是一样的，可以尝试自己做一做。

代码：

python

class Solution(object):
    def maxProfit(self, prices, fee):
        """
        :type prices: List[int]
        :type fee: int
        :rtype: int
        """
        dp = [[0, 0] for _ in range(len(prices))]

        dp[0][0] = 0 - prices[0]
        dp[0][1] = 0

        for i in range(1, len(prices)):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i])
            dp[i][1] = max(dp[i-1][1], prices[i] + dp[i-1][0] - fee)

        return dp[len(prices)-1][1]