一、引文

1 回归分析

回归是统计学上用来分析数据的方法，以了解两个或多个变量之前的关系。通常是建立被解释变量Y和解释变量X之间关系的模型。

回归分析的最早形式是最小二乘法。

勒让德和高斯都将该方法应用于从天文观测中确定关于太阳的物体的轨道（主要是彗星，但后来是新发现的小行星）的问题。高斯在1821年发表了最小二乘理论的进一步发展[3]，包括高斯－马尔可夫定理的一个版本。

但是，回归（regression）一词由法兰西斯·高尔顿（Francis Galton）所使用。

他在统计学方面也有贡献，高尔顿在1877年发表关于种子的研究结果，指出回归到平均值（regression toward the mean）现象的存在，这个概念与现代统计学中的“回归”并不相同，但是却是回归一词的起源。在此后的研究中，高尔顿第一次使用了相关系数（correlation coefficient）的概念。他使用字母“r”来表示相关系数，这个传统一直延续至今。

2 什么是线性（以下来自ChatGPT）

在数学和统计学中，线性是一个重要的概念，指的是与直线（线性函数）具有相似性质的关系或性质。一个数学对象被称为线性，通常满足以下两个性质：
1. 比例性质（Proportionality）：如果一个对象的变化与另一个对象的变化成正比，那么它们之间的关系就是线性的。换句话说，当一个对象发生变化时，另一个对象也以相同比例发生变化。
2. 叠加性质（Superposition）：如果一个对象的总效应等于多个独立影响的叠加，那么这个对象的关系是线性的。换句话说，系统的响应是各个独立输入的总和。
  .
在数学中，线性性质可以表示为以下形式：
1. 线性函数（Linear Function）：一个函数如果满足以下形式，就被称为线性函数：
  $f (a x + b y) = a f (x) + b f (y)$
  其中， $a$ 和 $b$ 是常数， $f (x)$ 和 $f (y)$ 是函数。
2. 线性方程（Linear Equation）：一个方程如果可以写成以下形式，就被称为线性方程：
  $a x + b y = c$
  其中， $a$ 、 $b$ 、 $c$ 是常数， $x$ 和 $y$ 是变量。

二、正文目录

1 线性回归

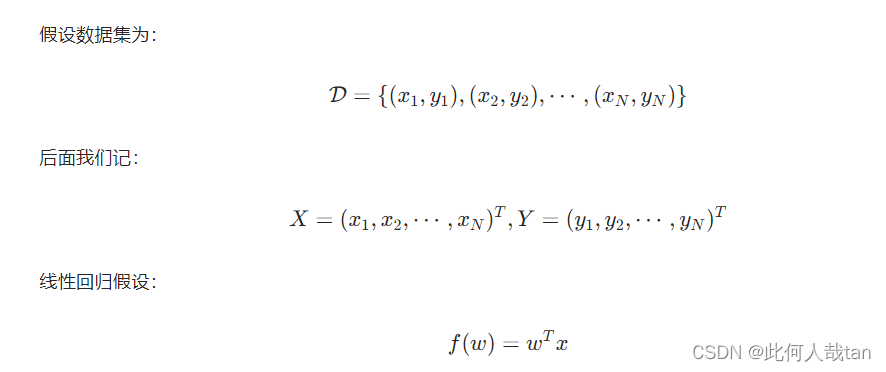
在这里插入图片描述

2 参数估计

2.1 最小二乘法

在这里插入图片描述

2.2 最大似然估计MLE

$\begin{aligned} L(w)=\log p(Y \mid X, w) & =\log \prod_{i=1}^{N} p\left(y_{i} \mid x_{i}, w\right) \\ & =\sum_{i=1}^{N} \log \left(\frac{1}{\sqrt{2 \pi \sigma}} e^{\left.-\frac{\left(y_{i}-w^{T} x_{i}\right)^{2}}{2 \sigma^{2}}\right)}\right. \\ \underset{w}{\operatorname{argmax} L(w)} & =\underset{w}{\operatorname{argmin}} \sum_{i=1^{N}}\left(y_{i}-w^{T} x_{i}\right)^{2} \end{aligned}$

2.3 最大后验估计MAP

$\begin{aligned} \hat{w}=\underset{w}{\operatorname{argmax}} p(w \mid Y) & =\underset{w}{\operatorname{argmax}} p(Y \mid w) p(w) \\ & =\underset{w}{\operatorname{argmax}} \log p(Y \mid w) p(w) \\ & =\underset{w}{\operatorname{argmax}}(\log p(Y \mid w)+\log p(w)) \\ & =\underset{w}{\operatorname{argmin}}\left[\left(y-w^{T} x\right)^{2}+\frac{\sigma^{2}}{\sigma_{0}^{2}} w^{T} w\right] \end{aligned}$

3 正则化

3.1 L1 正则化： Lasso 回归

3.2 L2 正则化： Ridge 回归

在这里插入图片描述

偷个懒，不重复造轮子了。主要是为了自己学习和回顾。以上相关推导公式来自视频和链接，在此感谢up主和博主的分享
Bilibili-机器学习白板系列之线性回归
机器学习-白板推导系列(三)-线性回归（Linear Regression）

三学习总结

1 清晰几个概念：

1.1 xx分不清

此外在回归分析中，会有残差和均方误差两个词。其中残差是预测值和观测值（真实标签）之差。

SSE 表示的是残差平方和（Sum of Squares for Error），也称为误差平方和。
MSE 表示均方误差（Mean Squared Error） 均方误差是残差平方和除以样本数量的结果，表示了每个样本的预测误差的平方的平均值

数学上的 误差（相对误差和绝对误差） 是实际测量值和真实值（理论值）之前的差别。
统计学上，方差是衡量数据的离散程度的，而偏差描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据。

1.2 权衡偏差和方差以最小化均方误差

偏差和方差度量着估计量的两个不同误差来源。偏差度量着偏离真实函数或参数的误差期望，而方差度量着数据上任意特定采样可能导致的估计期望的偏差 —花书《深度学习》

2 MAP 和 L2范数正则的关系

在噪声为高斯分布的时候，MLE 的解等价于最小二乘误差
加上L2正则项后，最小二乘误差加上 L2 正则项等价于权重先验分布为高斯分布的MAP解
加上 L1 正则项后，等价于权重Laplace 先验分布。

注意这里有两个分布:

一个是噪声（残差） 为高斯分布，有MLE等价于最小二乘误差。
另一个是 权重（参数） 的先验分布为高斯分布，有MAP等价于最小二乘误差加上 L2 正则化。

所谓的先验是针对后验 $p (w ∣ Y)$ 来说的。这里先假设权重（参数）的先验分布为高斯分布，至于为什么这样做，这里涉及到频率派和贝叶斯派的估计方法。------先不说了😂

其实，这里给最小二乘误差（均方误差）人为加上一个正则项，也是加上了一个先验的知识，倾向于L2范数较小的权重是。而这个先验知识，和假设权重先验分布为高斯分布的最大后验估计是等价的。— —那为什么呢？先留着🤣

3 线性回归的假设条件

前提条件包括：

误差项服从正态分布
误差的方差在各个自变量值上是恒定的（即同方差性，homoscedasticity）
自变量和误差项之间没有相关性
。。。。。。

其中 异方差性 可参考：
残差分析
残差分析与残差图

残差中的非随机模式表明模型的确定部分（预测变量）没有捕获一些“泄露”到残差中的一些可解释／可预测信息

也许线性回归模型只能用来分析一下较为简单的数据，但是线性回归却为其他传统机器学习方法提供了很好的思考方向。

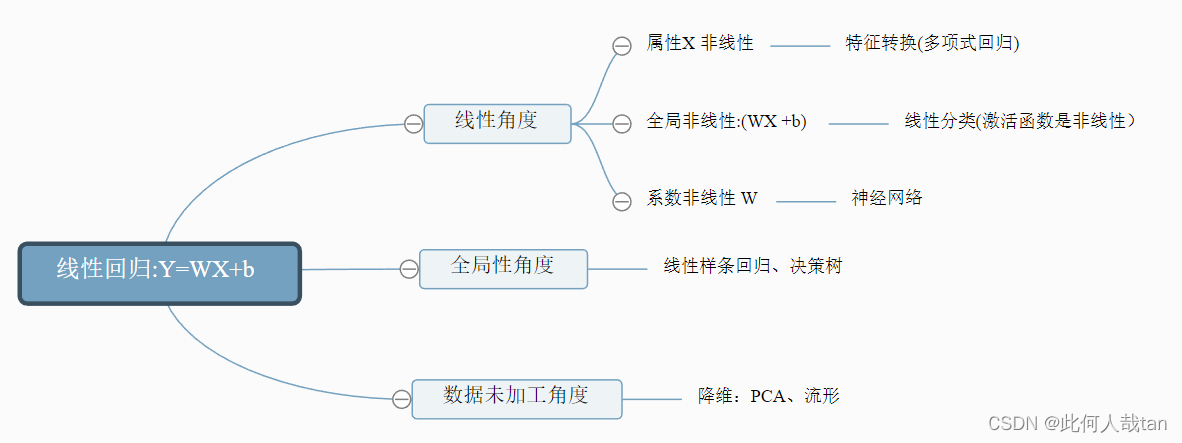
4 线性回归模型的不足：

线性模型往往不能很好地拟合数据，因此有三种⽅案克服这⼀劣势：

对特征的维数进⾏变换，例如多项式回归模型就是在线性特征的基础上加⼊⾼次项。
在线性⽅程后⾯加⼊⼀个⾮线性变换，即引⼊⼀个⾮线性的激活函数，典型的有线性分类模型如感知机。
对于⼀致的线性系数，我们进⾏多次变换，这样同⼀个特征不仅仅被单个系数影响，例如多层感知机（深度前馈⽹络）。

线性回归在整个样本空间都是线性的，我修改这个限制，在不同区域引⼊不同的线性或⾮线性，例如线性样条回归和决策树模型。
线性回归中使⽤了所有的样本，但是对数据预先进⾏加⼯学习的效果可能更好（所谓的维数灾难，⾼维度数据更难学习），例如 PCA 算法和流形学习

这里画个图，总结一下：
在这里插入图片描述