98. 验证二叉搜索树
文章目录
- [98. 验证二叉搜索树](https://leetcode.cn/problems/validate-binary-search-tree/)
- 一、题目
- 二、题解
- 方法一:区间划分递归
- 方法二:中序遍历
- 递归
- 迭代
一、题目
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
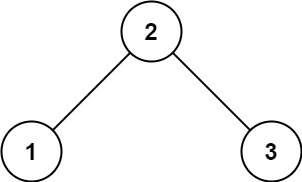
输入:root = [2,1,3]
输出:true
示例 2:
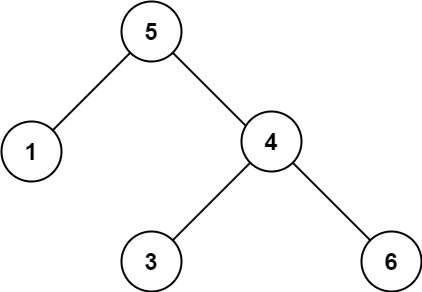
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在
[1, 104]内 -231 <= Node.val <= 231 - 1
二、题解
方法一:区间划分递归
们需要判断给定的二叉树是否是一个有效的二叉搜索树,而有效的二叉搜索树有以下特点:
- 节点的左子树只包含小于当前节点的值。
- 节点的右子树只包含大于当前节点的值。
- 所有左子树和右子树也必须是有效的二叉搜索树。
算法思路(结合下面代码):
我们可以考虑用递归的方式来解决这个问题。对于每个节点,我们需要检查它是否满足二叉搜索树的性质,即左子树中的节点都小于当前节点,右子树中的节点都大于当前节点。
为了实现这个递归算法,我们可以定义一个递归函数 isValidBSTHelper,它会传入当前节点、一个最小节点和一个最大节点。初始调用时,最小节点和最大节点可以设为 nullptr,表示没有限制。
在递归函数内部,我们首先检查当前节点是否为空,如果为空,说明这个子树是一个有效的二叉搜索树,返回 true。
然后,我们检查当前节点的值是否在最小节点和最大节点的范围内。如果不在范围内,说明不满足二叉搜索树的性质,返回 false。
接着,我们递归地调用 isValidBSTHelper 函数,传入左子节点以及当前节点作为最大节点(因为左子树中的节点都应该小于当前节点),同时传入最小节点不变。
同样地,我们递归地调用 isValidBSTHelper 函数,传入右子节点以及当前节点作为最小节点(因为右子树中的节点都应该大于当前节点),同时传入最大节点不变。
最后,我们将左子树和右子树的验证结果进行逻辑与操作,如果都为 true,说明当前子树是一个有效的二叉搜索树,返回 true;否则,返回 false。
具体实现:
class Solution {
public:
bool isValidBST(TreeNode* root) {
return isValidBSTHelper(root, nullptr, nullptr);
}
private:
bool isValidBSTHelper(TreeNode* node, TreeNode* minNode, TreeNode* maxNode) {
if (node == nullptr) {
return true;
}
if ((minNode && node->val <= minNode->val) || (maxNode && node->val >= maxNode->val)) {
return false;
}
bool left_isValid = isValidBSTHelper(node->left, minNode, node);
bool right_isValid = isValidBSTHelper(node->right, node, maxNode);
return left_isValid && right_isValid;
}
};
算法分析:
-
时间复杂度:在最坏情况下,我们需要遍历每个节点一次,所以时间复杂度是 O(n),其中 n 是节点数目。
-
空间复杂度:递归的深度取决于树的高度,最坏情况下是 O(n),因为树可以退化成链表。递归过程中使用的额外空间是常数级别的,所以总的空间复杂度也是 O(n)。
方法二:中序遍历
二叉搜索树在中序遍历中是单调递增的,那么我们可以修改一下中序遍历的代码来判断这是否是二叉搜索树
递归
class Solution {
public:
long max = LONG_MIN; // 初始化为最小值
bool isValidBST(TreeNode* root) {
if (root == nullptr)
return true;
// 递归检查左子树
bool left = isValidBST(root->left);
// 检查当前节点的值是否大于之前的最大值
if (root->val > max) {
max = root->val;
} else {
return false;
}
// 更新最大值后,递归检查右子树
bool right = isValidBST(root->right);
return left && right;
}
};
迭代
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL; // 记录前一个节点
while (cur != NULL || !st.empty()) {
if (cur != NULL) {
st.push(cur);
cur = cur->left; // 左
} else {
cur = st.top(); // 中
st.pop();
if (pre != NULL && cur->val <= pre->val)
return false;
pre = cur; //保存前一个访问的结点
cur = cur->right; // 右
}
}
return true;
}
};