罗勇军 → 《算法竞赛·快冲300题》每日一题：“推箱子” ← 差分及前缀和

【题目来源】
http://oj.ecustacm.cn/problem.php?id=1819
http://oj.ecustacm.cn/viewnews.php?id=1023

【题目描述】
在一个高度为H的箱子前方，有一个长和高为N的障碍物。
障碍物的每一列存在一个连续的缺口，第i列的缺口从第l个单位到第h个单位（从底部由0开始数）。
现在请你清理出一条高度为H的通道，使得箱子可以直接推出去。
请输出最少需要清理的障碍物面积。
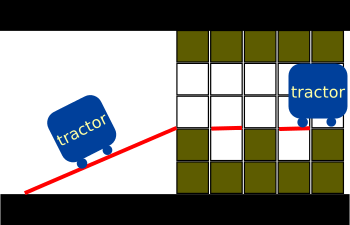
如下图为样例中的障碍物，长和高度均为5，箱子高度为2。不需要考虑箱子会掉入某些坑中。最少需要移除两个单位的障碍物可以造出一条高度为2的通道。

【输入格式】
输入第一行为两个正整数N和H，表示障碍物的尺寸和箱子的高度，1≤H≤N≤1000000。
接下来N行，每行包含两个整数li和hi，表示第i列缺口的范围，0≤li≤hi<N。

【输出格式】
输出一个数字表示答案。

【输入样例】
5 2
2 3
1 2
2 3
1 2
2 3

【输出样例】
2

【算法分析】
一、本题箱子高度为H，障碍物的尺寸为N*N，若用 a[i] 表示障碍物第 i 行的空白数量，则问题就抽象为“从 a[] 中找出连续的 H个整数，要求它们的和最大”，也即要清理的障碍物面积最小。很显然，此时问题就转化成一个典型的区间求和问题。而区间求和问题，自然而然就要考虑选择差分和前缀和进行优化，避免时间复杂度过大而超时。

二、本题数据规模较大，计算结果会超过 10 位数。故保险起见，选择 long long 数据类型。

三、本题需用差分和前缀和来优化代码，避免超时。差分与前缀和是一对互逆的操作，常用于求解区间问题。
1.差分主要用于多次对区间进行加减操作的问题。
差分算法涉及的主要操作陈述如下：
（1）构建差分数组
【差分数组概念】设原数组为含有 n 个数的 a 数组（下标常从 1 开始），差分数组为 d 数组（下标常从 1 开始）。其中，令 d[1]=a[1]，且对于 i∈[2,n]，令 d[i]=a[i]-a[i-1]。
【示例】例如，设原数组 a[]=[3 5 9 10 16 18 27] （下标常从 1 开始），则有：
d[1]=a[1]=3，
d[2]=a[2]-a[1]=5-3=2，
d[3]=a[3]-a[2]=9-5=4，
d[4]=a[4]-a[3]=10-9=1，
d[5]=a[5]-a[4]=16-10=6，
d[6]=a[6]-a[5]=18-16=2，
d[7]=a[7]-a[6]=27-18=9，
即差分数组为 d[]=[3 2 4 1 6 2 9]。
（2）对原数组的区间 [le, ri] 进行加减操作
【结论】构造差分数组后，对原数组的区间 [le, ri] 的加减操作就转化为对差分数组的区间端点的操作：d[le]+=x，d[ri+1]-=x。显然，这大大降低了算法的时间复杂度。
【示例】例如，对原数组 a[]=[3 5 9 10 16 18 27] （下标常从 1 开始）的区间 [2,5] 中的每个数都加 3，则等价于执行d[2]+=3，d[5+1]-=3。
【解析】现在，来分析一下对原数组 a[]=[3 5 9 10 16 18 27] （下标常从 1 开始）执行 d[2]+=3，d[5+1]-=3 后，是否等价于对原数组的区间 [2,5] 中的每个数都加了 3？
由上文分析知，原数组 a[]=[3 5 9 10 16 18 27] 的差分数组为 d[]=[3 2 4 1 6 2 9]。显然，执行 d[2]+=3，d[5+1]-=3 后，原数组的差分数组由 d[]=[3 2 4 1 6 2 9] 变为 d[]=[3 5 4 1 6 -1 9]。
显然，由关系 d[1]=a[1]，d[i]=a[i]-a[i-1] （i≥2），知：
a[1]=d[1]=3
a[2]=d[2]+a[1]=5+3=8
a[3]=d[3]+a[2]=4+8=12
a[4]=d[4]+a[3]=1+12=13
a[5]=d[5]+a[4]=6+13=19
a[6]=d[6]+a[5]=-1+19=18
a[7]=d[7]+a[6]=9+18=27
可见，对原数组 a[]=[3 5 9 10 16 18 27] （下标常从 1 开始）执行 d[2]+=3，d[5+1]-=3 后，原数组变为 a[]=[3 8 12 13 19 18 27]，原数组区间 [2,5] 内的每个元素确实都加了3。
（3）对原数组的多个区间进行加减操作
【示例】例如，对原数组 a[]=[3 5 9 10 16 18 27] （下标常从 1 开始）的区间 [2,5] 中的每个数都加 3，则等价于执行d[2]+=3，d[5+1]-=3。然后，对区间 [3,6] 中的每个数都减 2（相当于加 -2），则等价于执行 d[3]+=(-2)，d[6+1]-=(-2)。最后，对区间 [1,4] 中的每个数都加 5，则等价于执行d[1]+=5，d[4+1]-=5。
【解析】由上文分析知，原数组 a[]=[3 5 9 10 16 18 27] 的差分数组为 d[]=[3 2 4 1 6 2 9]。
执行 d[2]+=3，d[5+1]-=3 后，由 d[]=[3 2 4 1 6 2 9] 变为 d[]=[3 5 4 1 6 -1 9]。
执行 d[3]+=(-2)，d[6+1]-=(-2) 后，由 d[]=[3 5 4 1 6 -1 9] 变为 d[]=[3 5 2 1 6 -1 11]。
执行 d[1]+=5，d[4+1]-=5 后，由 d[]=[3 5 2 1 6 -1 11] 变为 d[]=[8 5 2 1 1 -1 11]。
然后，仅观察最后生成的差分数组 d[]=[8 5 2 1 1 -1 11]，且依据关系 d[1]=a[1]，d[i]=a[i]-a[i-1] （i≥2），知：
a[1]=d[1]=8
a[2]=d[2]+a[1]=5+8=13
a[3]=d[3]+a[2]=2+13=15
a[4]=d[4]+a[3]=1+15=16
a[5]=d[5]+a[4]=1+16=17
a[6]=d[6]+a[5]=-1+17=16
a[7]=d[7]+a[6]=11+16=27
即，经过多轮对原数组的差分数组端点进行操作后，原数组 a[]=[8 13 15 16 17 16 27]。
为了验证比较，现在按上文对原数组 a[]=[3 5 9 10 16 18 27] 给定的区间进行操作的内容如下：
对区间 [2,5] 中的每个数都加 3，由 a[]=[8 13 15 16 17 16 27] 变为 a[]=[3 8 12 13 19 18 27]。
对区间 [3,6] 中的每个数都减 2，由 a[]=[3 8 12 13 19 18 27] 变为 a[]=[3 8 10 11 17 16 27]。
对区间 [1,4] 中的每个数都加 5，由 a[]=[3 8 10 11 17 16 27] 变为 a[]=[8 13 15 16 17 16 27]。
显然，与利用差分数组算出来的结果一样。
可见，若给定的原数组序列特别长，则差分数组对端点的操作将比原数组对区间的操作在得到计算结果上快得多，虽然它俩在计算结果上是一样的。
2.前缀和主要用于多次对区间进行求和的问题。
前缀和，无论是一维前缀和还是二维前缀和，通常都用于快速对区间进行求和。它们的思想都是利用给定的数据预先处理出一个前缀和数组 sum[]，之后在计算区间和的时候查表，从而可以大大降低算法的时间复杂度。参见：https://blog.csdn.net/hnjzsyjyj/article/details/120265452
一维前缀和数组预处理过程：sum[i]=sum[i-1]+a[i]
一维区间和计算过程：sum[y]-sum[x-1] （y≥x）
二维前缀和数组预处理过程：sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]
二维区间和计算过程：sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1] （y2≥y1，x2≥x1）

四、题目中陈述每一列存在一个连续的缺口，所以用暴力法统计此连续的缺口中的空白数量，计算量将会达到 O(NH)。由于 N 和 H 的数据量最高都可达到10^6，所以 NH 的规模将可能会超过 10^12，显然暴力法会超时。因此，需要利用差分算法将对连续区间的求和操作转化为对区间端点的操作，必然大大降低算法的时间复杂度。
本题中，对连续区间的差分操作（即构建差分方程）见如下代码：

int li,hi;
for(int i=1; i<=n; i++) { //Create differential array
    scanf("%d %d",&li,&hi);
    d[li]+=1; //d[li]++;
    d[hi+1]-=1; //d[hi+1]--;
}

可见，对区间的差分操作必须是对连续区间进行操作的。

五、在连续区间上应用差分算法的常见步骤：差分数组 → 原数组 → 前缀和
（1）对连续区间 [le,ri] 利用“d[le]+=1; d[ri+1]-=1;”构造差分数组d[]；
（2）利用“d[1]=a[1]，且对于 i∈[2,n]，d[i]=a[i]-a[i-1]”构造原数组a[]；
（3）利用“sum[i]=sum[i-1]+a[i]”构造前缀和数组sum[]。

【算法代码】

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int maxn=1e6+5;
ll d[maxn]; //differential array
ll a[maxn]; //number of obstacle's blank
ll sum[maxn]; //prefix sum

int main() {
    int n,h;
    scanf("%d %d",&n,&h);

    int li,hi;
    for(int i=1; i<=n; i++) { //Create differential array
        scanf("%d %d",&li,&hi);
        d[li]+=1; //d[li]++;
        d[hi+1]-=1; //d[hi+1]--;
    }

    for(int i=1; i<=n; i++) a[i]=a[i-1]+d[i-1];
    for(int i=1; i<=n; i++) sum[i]=sum[i-1]+a[i];

    ll ans=sum[h-1];
    for(int i=1; i+h-1<=n; i++) {
        ans=max(ans,sum[i+h-1]-sum[i-1]);
    }

    cout<<(ll)n*h-ans<<endl;
    return 0;
}


/*
in:
5 2
2 3
1 2
2 3
1 2
2 3

out:
2
*/

【参考文献】
https://blog.csdn.net/weixin_43914593/article/details/131730112
http://oj.ecustacm.cn/viewnews.php?id=1023
https://blog.csdn.net/weixin_43914593/category_12377073.html
https://blog.csdn.net/m0_51769031/article/details/123973620
https://www.cnblogs.com/jue1e0/p/15065006.html
https://blog.csdn.net/weixin_54442315/article/details/122663584