文章目录
- 前言
- 一、Harris 角点检测
- 二、SIFT
- 1、关键点定位 keypoint localisation
- 2、特征描述 feature description
前言
本文为12月13日 OpenCV 实战基础学习笔记,分为两个章节:
- Harri 角点检测;
- SIFT。
一、Harris 角点检测
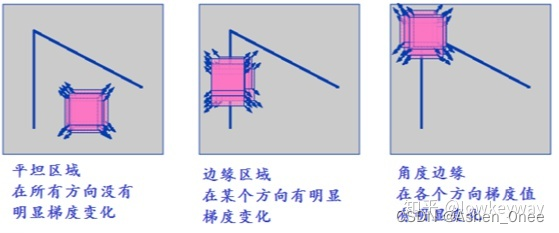
使用一个固定窗口在图像上进行任意方向上的滑动,比较滑动前与滑动后两种情况,窗口中的像素灰度变化程度,如果存在任意方向上的滑动,都有着较大灰度变化,那么我们可以认为该窗口中存在角点。
1、公式推导
设窗口平移
[
U
,
V
]
[U, V]
[U,V] 产生灰度变化
E
(
u
,
v
)
E(u, v)
E(u,v) :
E
(
u
,
v
)
=
∑
x
,
y
w
(
x
,
y
)
[
I
(
x
+
u
,
y
+
v
)
−
I
(
x
,
y
)
]
2
E(u,v) = {\textstyle \sum_{x, y}} w(x, y)[I(x+u, y+v) - I(x, y)]^2
E(u,v)=∑x,yw(x,y)[I(x+u,y+v)−I(x,y)]2
其中:
- u , v u, v u,v: 窗口偏移量;
- x , y x, y x,y: 窗口内像素的坐标;
- w ( x , y ) w(x, y) w(x,y): 窗口函数,内含权重信息,常用的有权重为1和呈二元高斯正太分布的权重;
- I I I: 像素密度函数,类比与像素值.
2、找到 E ( u , v ) E(u, v) E(u,v) 的最大值
- 泰勒展开式:
f ( x + u , y + v ) ≈ f ( x , y ) + u f x ( x , y ) + v f y ( x , y ) f(x+u, y+v) \approx f(x, y) + uf_x(x, y) + vf_y(x, y) f(x+u,y+v)≈f(x,y)+ufx(x,y)+vfy(x,y)
所以:
∑
[
I
(
x
+
u
,
y
+
v
)
−
I
(
x
,
y
)
]
2
≈
∑
[
I
(
x
,
y
)
+
u
I
x
(
x
,
y
)
+
v
I
y
(
x
,
y
)
−
I
(
x
,
y
)
]
2
=
∑
u
2
I
x
2
+
2
v
u
I
x
I
y
+
v
2
I
y
2
=
∑
[
u
v
]
[
I
x
2
I
x
I
y
I
x
I
y
I
y
2
]
[
u
v
]
M
=
∑
x
,
y
w
(
x
,
y
)
[
I
x
2
I
x
I
y
I
x
I
y
I
y
2
]
\sum [I(x+u, y+v) - I(x, y)]^2 \approx \sum [ I(x, y) + uI_x(x, y) + vI_y(x, y)- I(x, y)]^2 = \sum u^2 I_x^2 + 2vu I_x I_y + v^2 I_y^2 = \sum [uv]\begin{bmatrix} I_x^2 & I_x I_y \\ I_x I_y & I_y^2 \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix}\\ M = {\textstyle \sum_{x, y}}w(x, y) \begin{bmatrix} I_x^2 & I_x I_y \\ I_x I_y & I_y^2 \end{bmatrix}
∑[I(x+u,y+v)−I(x,y)]2≈∑[I(x,y)+uIx(x,y)+vIy(x,y)−I(x,y)]2=∑u2Ix2+2vuIxIy+v2Iy2=∑[uv][Ix2IxIyIxIyIy2][uv]M=∑x,yw(x,y)[Ix2IxIyIxIyIy2]
其中, ∑ x , y w ( x , y ) {\textstyle \sum_{x, y}}w(x, y) ∑x,yw(x,y) 为窗口功能, I x , I y I_x, I_y Ix,Iy 分别为每个像素点 x 方向的强度和 y 方向的强度。 对 I x , I y I_x, I_y Ix,Iy 求偏导得:
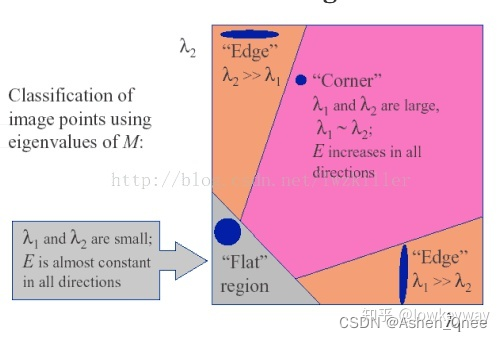
- λ 1 \lambda_1 λ1: X 轴方向的偏导的特征值;
- λ 2 \lambda_2 λ2: Y 轴方向的偏导的特征值.
- 代码如下:
cv2.cornerHarris()
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
img = cv.imread("./Harris_SIFT/test_1.jpg")
# img = cv.cvtColor(img, cv.COLOR_BGR2RGB)
cv.imshow("Origin", img)
cv.waitKey(0)
cv.destroyAllWindows()

img_gray = cv.cvtColor(img, cv.COLOR_RGB2GRAY)
# img_gray = np.float32(img_gray)
dst = cv.cornerHarris(img_gray, 2, 3, 0.04)
print("dst.shape: ", dst.shape)
>>> dst.shape: (800, 1200)
img[dst > 0.01 * dst.max()] = [0, 0, 255]
cv.imshow("Dst", img)
cv.waitKey(0)
cv.destroyAllWindows()

二、SIFT
Scale-Invariant Feature Transform. 步骤主要分两步:
-
- 关键点定位 keypoint localisation;
-
- 特征描述 feature description.
1、关键点定位 keypoint localisation
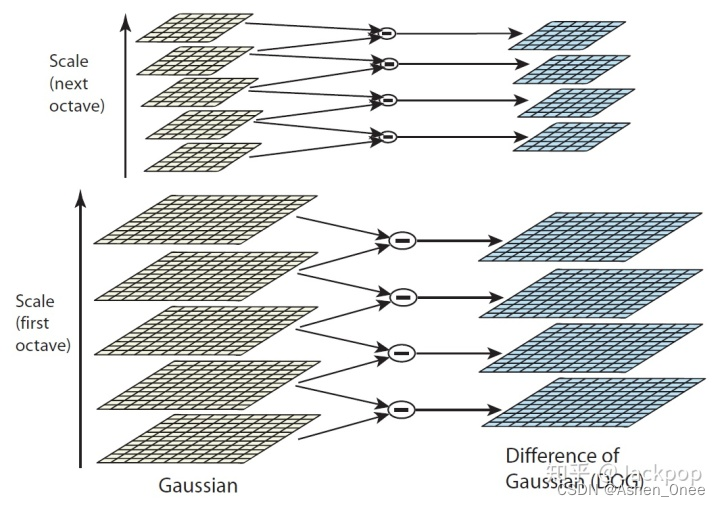
- 尺度空间极值检测: 通过使用高斯差分函数来计算并搜索所有尺度上的图像位置,用于识别对尺度和方向不变的潜在兴趣点。
-
DoG空间极值检测: 将每个像素点和其图像域(同一尺度空间)和尺度域(相邻的尺度空间)的所有相邻点进行比较。
当其大于(或者小于)所有相邻点时,该点就是极值点。
中间的检测点要和其所在图像的 3 × 3 3\times 3 3×3 邻域 8 个像素点,以及其相邻的上下两层的 3 × 3 3\times 3 3×3 领域 18 个像素点,共 26 个像素点进行比较。 -
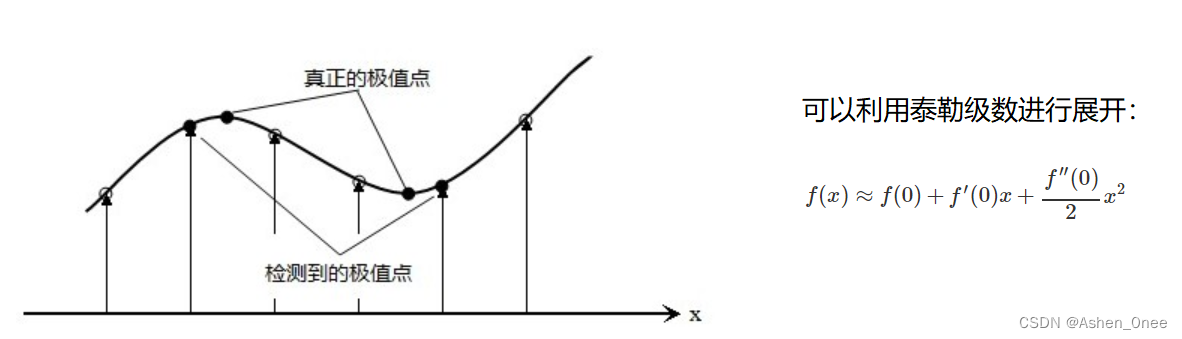
关键点精确定位: 通过一个拟合精细的模型在每个候选位置上确定位置和尺度,关键点的选择依赖于它们的稳定程度。
- 方向匹配: 基于局部图像的梯度方向,为每个关键点位置分配一个或多个方向,后续所有对图像数据的操作都是相对于关键点的方向、尺度和位置进行变换,从而而这些变换提供了不变形。
2、特征描述 feature description
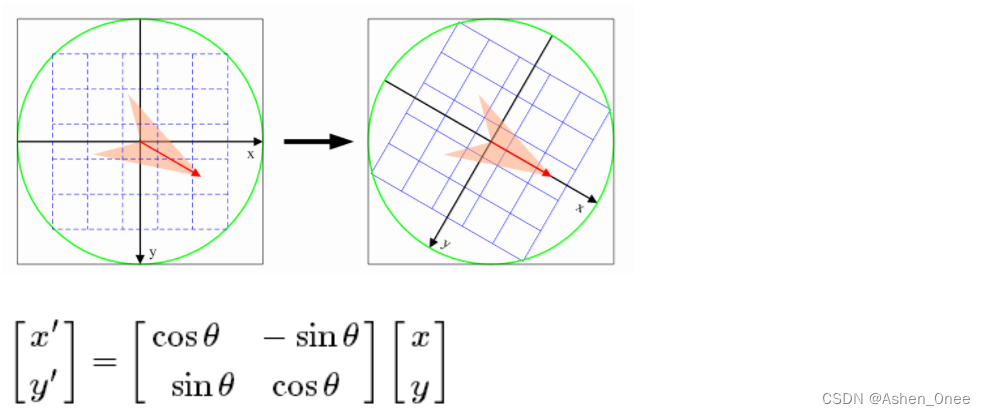
- 使用直方图统计邻域内像素的梯度和方向:

为了保证特征矢量的旋转不变性,要以特征点为中心,在附近邻域内将坐标轴旋转θ角度,即将坐标轴旋转为特征点的主方向。
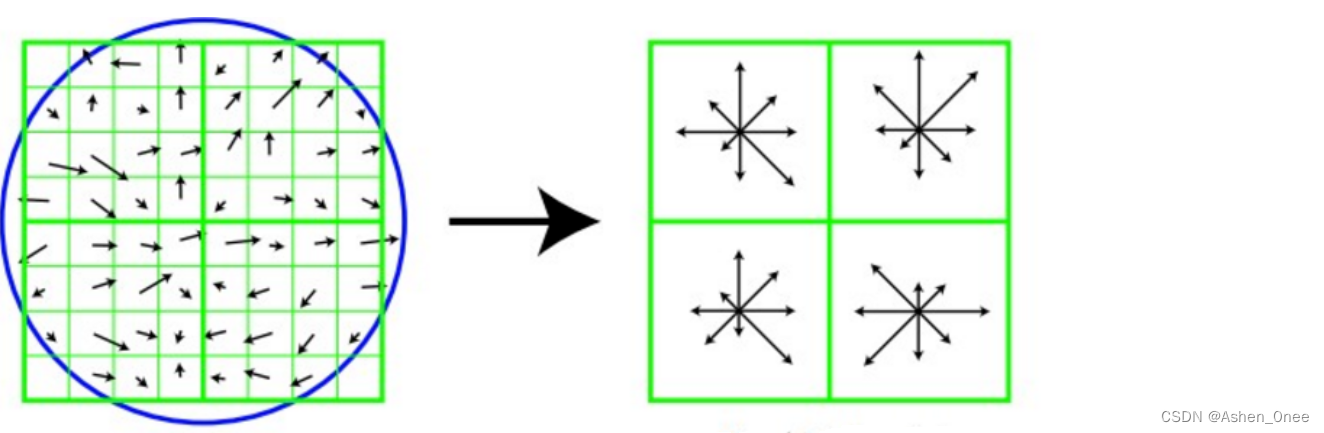
旋转之后的主方向为中心取
8
×
8
8\times 8
8×8 的窗口,求每个像素的梯度幅值和方向,箭头方向代表梯度方向,长度代表梯度幅值,然后利用高斯窗口对其进行加权运算,最后在每个
4
×
4
4\times 4
4×4 的小块上绘制 8 个方向的梯度直方图,计算每个梯度方向的累加值,即可形成一个种子点,即每个特征的由 4 个种子点组成,每个种子点有 8 个方向的向量信息。
- 代码如下:
import cv2 as cv
import numpy as np
img = cv.imread("./Harris_SIFT/test_1.jpg")
img_gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
cv.imshow("Gray", img_gray)
cv.waitKey(0)
cv.destroyAllWindows()

# 得到特征点
sift = cv.SIFT_create()
kp = sift.detect(img_gray, None)
img = cv.drawKeypoints(img_gray, kp, img)
cv.imshow("Keypoints", img)
cv.waitKey(0)
cv.destroyAllWindows()

# 计算特征
kp, des = sift.compute(img_gray, kp)
print(np.array(kp).shape)
des.shape
>>> (6809, 128)








![[036]基于Vue+Nodejs的网上作业批改系统(含源码、数据库、万字课设报告)](https://img-blog.csdnimg.cn/9b1b3923f13d4601ab4f0d3a3549b9ce.png)