Problem - D - Codeforces

 

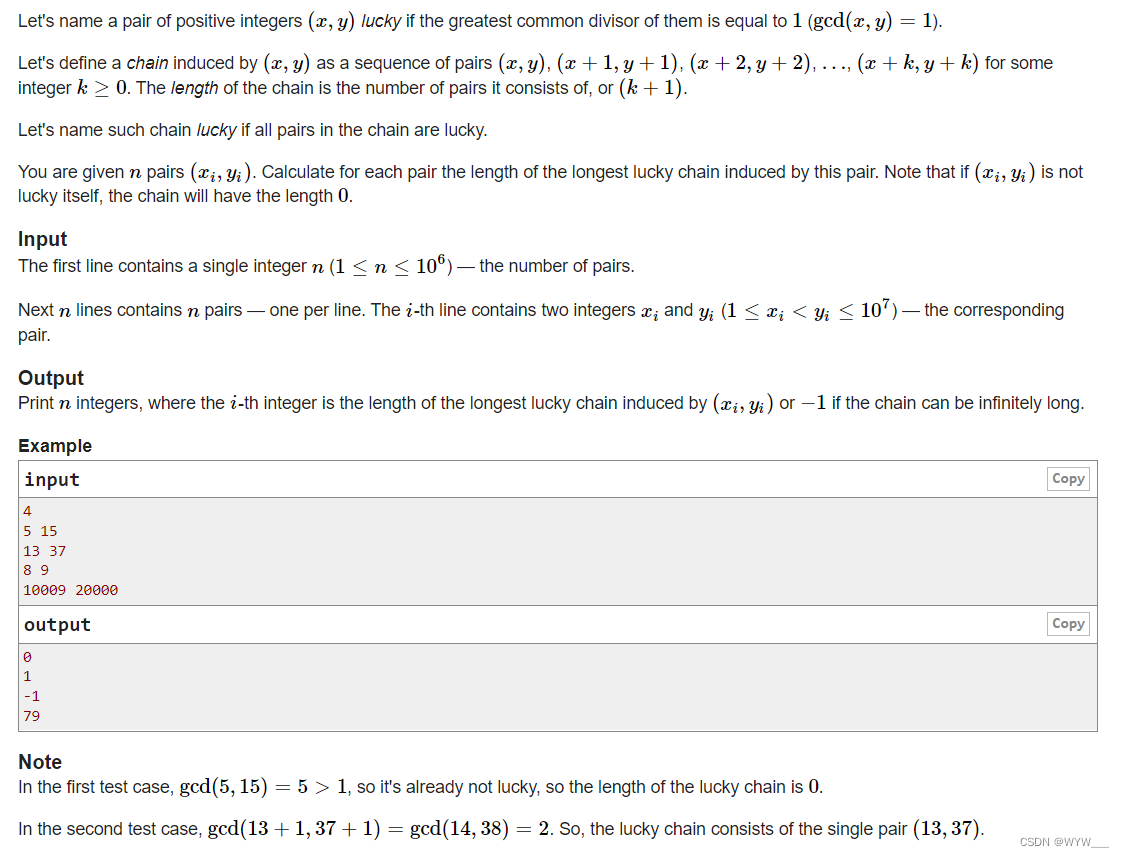
如果一对正整数(x,y)的最大公除数等于1(gcd(x,y)=1)，我们就把它们命名为幸运。

让我们把由(x,y)引起的链定义为一个由(x,y), (x+1,y+1), (x+2,y+2), ..., (x+k,y+k)组成的序列，对于某个整数k≥0。

如果链中的所有配对都是幸运的，我们就把这种链称为幸运链。

给你n对(xi,yi)。为每一对计算由这一对引起的最长的幸运链的长度。请注意，如果(xi,yi)本身不是幸运的，那么该链的长度为0。

输入
第一行包含一个整数n（1≤n≤106）--配对的数量。

接下来的n行包含n个配对--每行一个。第i行包含两个整数xi和yi（1≤xi<yi≤107）--对应的配对。

输出
打印n个整数，其中第i个整数是由(xi,yi)引起的最长的幸运链的长度，如果该链可以无限长，则为-1。

例子
输入复制
4
5 15
13 37
8 9
10009 20000
输出拷贝
0
1
-1
79
注意
在第一个测试案例中，gcd(5,15)=5>1，所以它已经不幸运了，所以幸运链的长度是0。

在第二个测试案例中，gcd(13+1,37+1)=gcd(14,38)=2。所以，幸运链由单对（13,37）组成。

题解:
gcd(a,b) = gcd(a ,a - b)

gcd(a+k,b+k) = gcd(a+k,b - a)

设w = abs(a - b)

题目目转化为了a加多少gcd(a+k,w) != 1

我们分解质因数w,遍历w的质因数所有质因数x

找到最小的x - a%x

#include<iostream>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<map>
#include<cstring>
#include<cmath>
using namespace std;
#define int long long
int f[10000060];
int p[10000600];
int cnt = 0;
void solve()
{
	int a,b;
	cin >> a >> b;
	int k = abs(a - b);
	if(k == 1)
	{
		cout<<"-1\n";
		return ;
	}
	if(__gcd(a,b) != 1)
	{
		cout<<0<<"\n";
		return ;
	}
	int ans = 1e9;
	while(k > 1)
	{
//		cout<<1<<"\n";
		ans = min(ans,p[k] - a%p[k]);
		int tt = p[k];
		while(k%tt == 0)
		k /= tt; 
	}
	cout << ans<<"\n";
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int t = 1;
	cin >> t;
	for(int i = 2;i <= 10000000;i++)
	{
		if(!p[i])
		{
			f[++cnt] = i,p[i] = i;
		}
		for(int j = 1;j <= cnt&&f[j]*i <= 10000000;j++)
		{
			p[i*f[j]] = f[j];
			if(i%f[j] == 0)
			break;
		}
	}
    while(t--)
	{
		solve();
	} 
}
//WBBW
//B