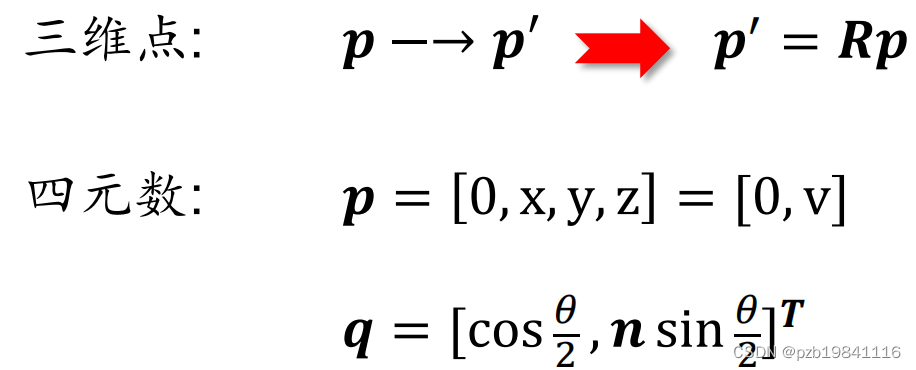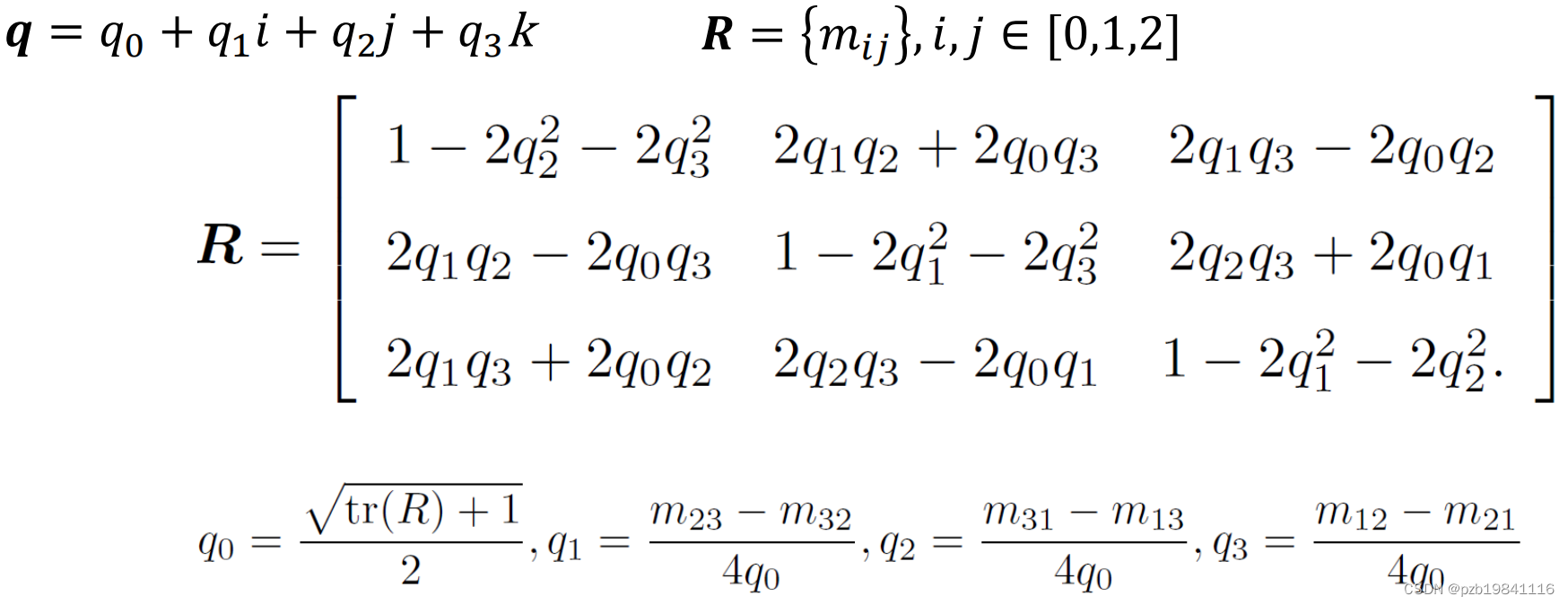空间数据的表达方式:点和向量两种形式。
向量的内积,也叫做点乘,是逐点相乘后累加,最终结果是一个标量,物理意义是一个向量在另一个向量上的投影。
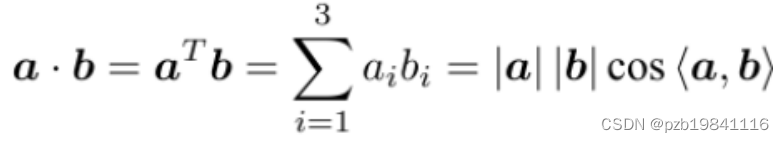
外积,也叫做叉乘,两个向量拼起来成,结果是一个矩阵,物理意义是旋转。
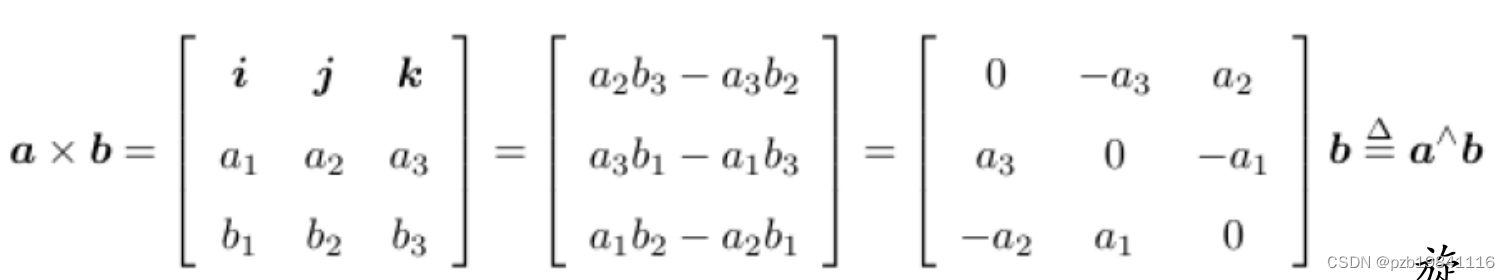
向量旋转
向量旋转可以由旋转轴向量加角度表示,一般采用右手坐标系。
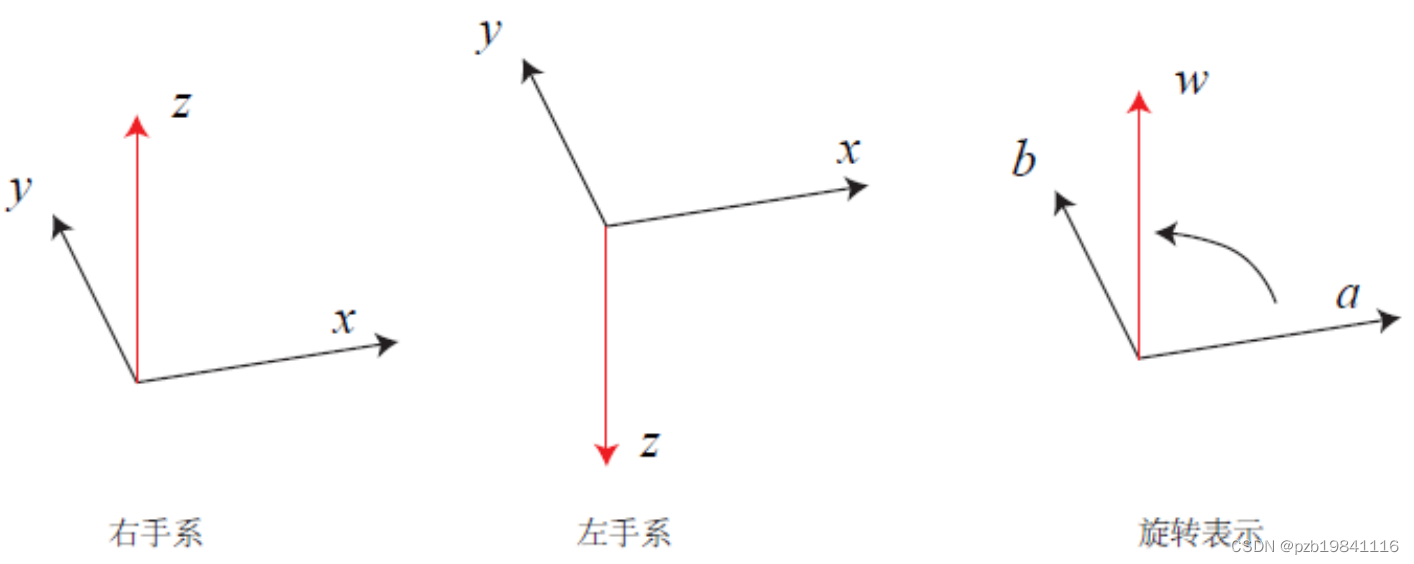
a到b的旋转可以由向量w来描述
坐标系的变换包括平移和旋转,平移是对原点的平移,旋转是绕着三个轴旋转。
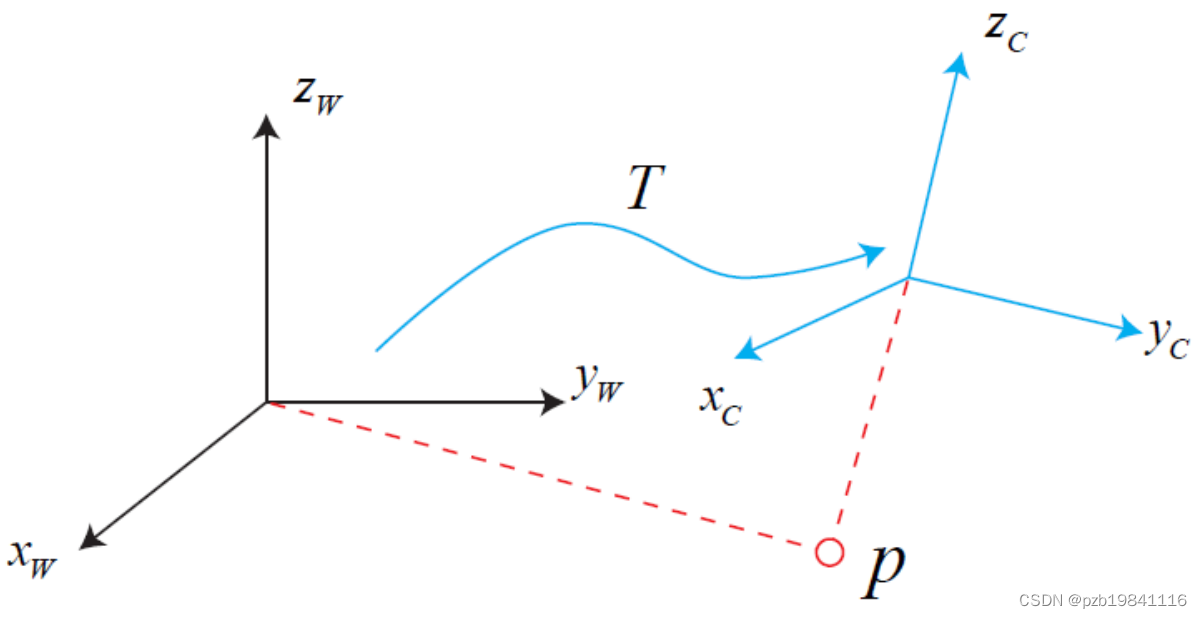
刚体运动:在三维空间中,把一个几何不变物体作旋转、平移的运动叫刚体运动。
刚体运动包括平移T和旋转R。
坐标系发生旋转,原坐标系下向量的值,按下面的方式进行变换。

这个矩阵一般叫旋转矩阵R,其必要条件是行列式为1的正交矩阵。
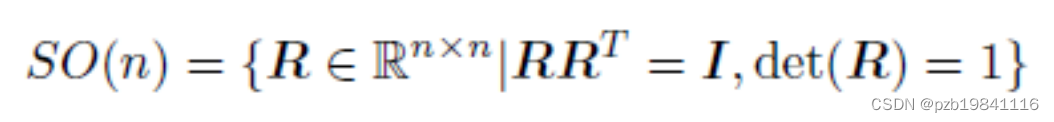
SO(n)
是特殊正交群:Special Orthogonal Group
旋转矩阵为正交阵,它的逆(即转置)描述了一个相反的旋转

旋转平移矩阵
世界坐标系中的向量a,经过一次旋转(R)和平移(t)后,得到了a':
𝑎′= 𝑅𝑎 + 𝑡 这里的t为平移向量。
将平移向量放进 矩阵运算中,则原向量变成齐次向量,矩阵变成了变换矩阵。
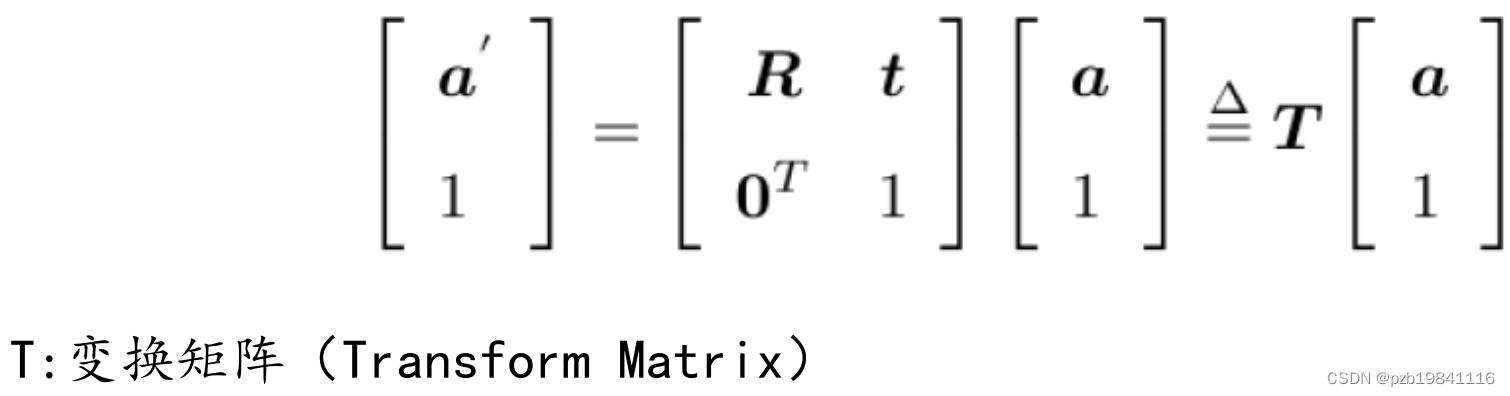
特殊欧式群:变换矩阵具有如下的特性。
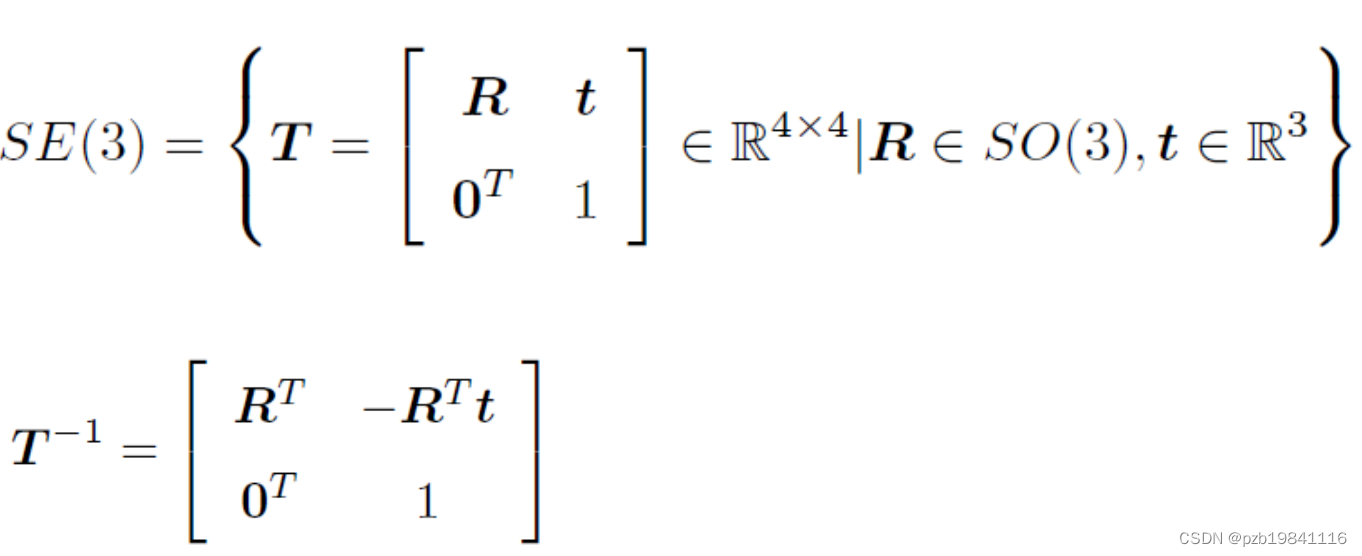
罗德里格公式:
假设有一个旋转轴为n,角度为θ的旋转,显然,它对应的旋转向量为θn。
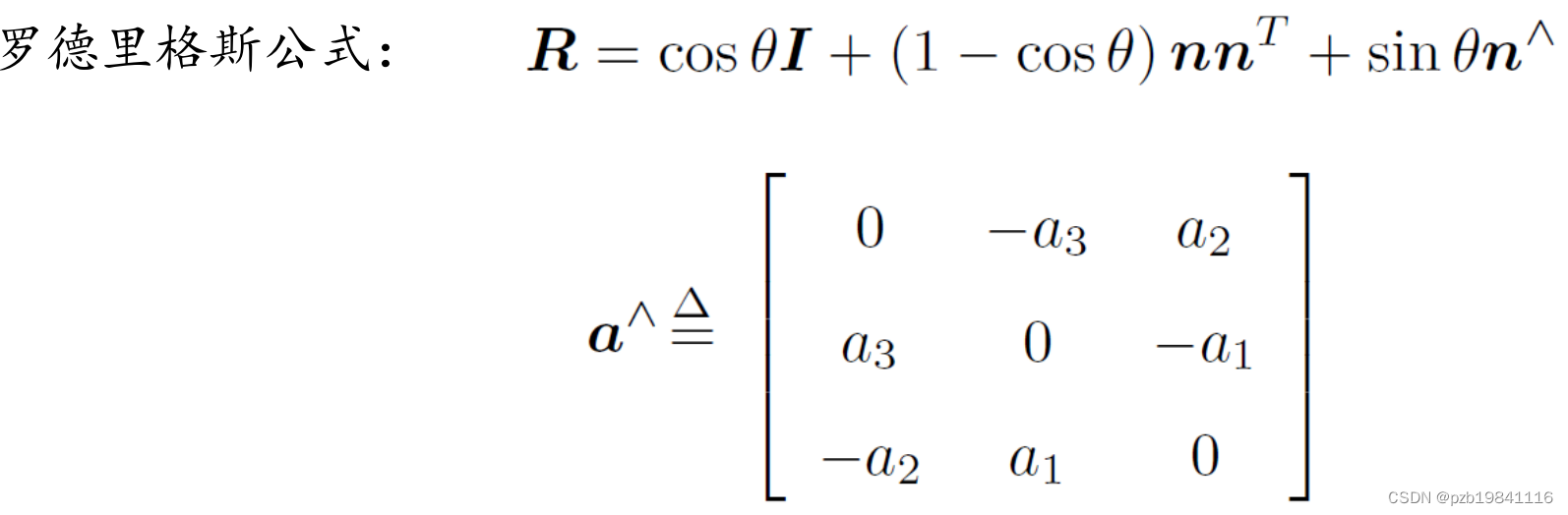
从一个旋转矩阵到旋转向量的转换。对于转角θ:

欧拉角:
用三个角度描述一个刚体在三维空间中的姿态,偏航-俯仰-滚转: yaw-roll-pitch → z-x-y。

欧拉角的缺点:万向锁。
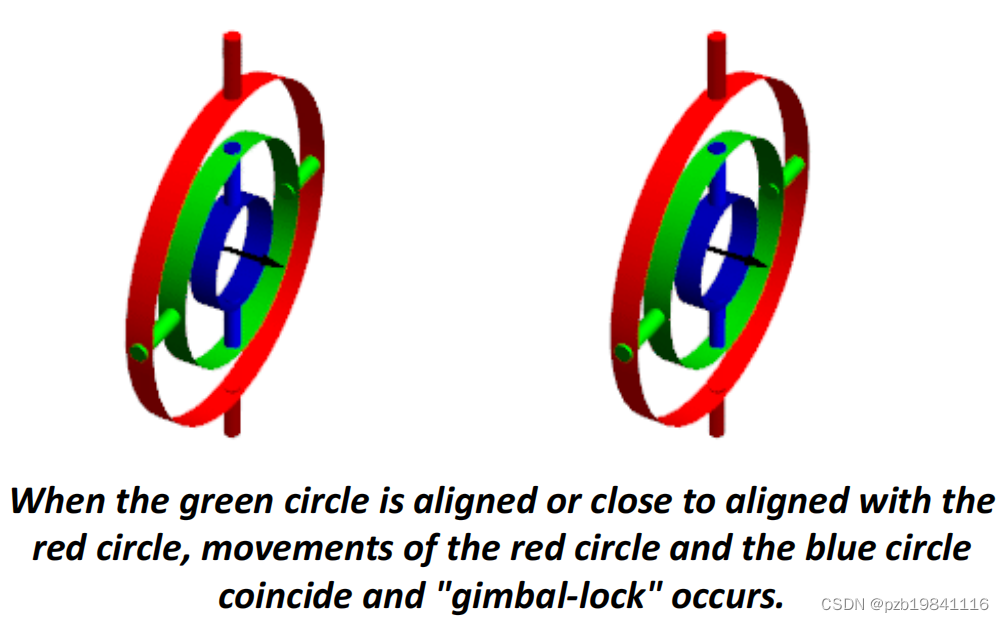
当某一个轴旋转90°,有两个轴的对应平面重合,则此情况下两个旋转的效果是一样的,这种情况叫做万向锁。
为了避免万向锁对旋转计算的影响,SLAM中一般使用四元数来提起欧拉角描述旋转,当然本质是一样的。
一个四元数q 拥有一个实部和三个虚部:
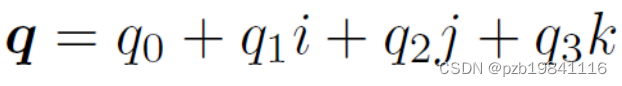
三个虚部之间的运算关系:
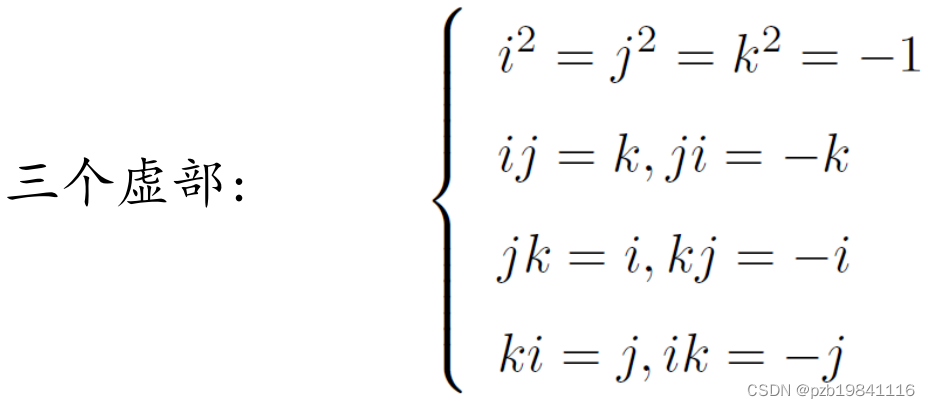
也可以用一个标量和一个向量来表达四元数:
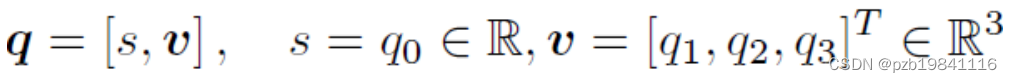
四元数的四则运算:
设𝒒𝒂 = [𝑠𝑎, 𝑣𝑎] , 𝒒𝒃 = [𝑠𝑏, 𝑣𝑏],则
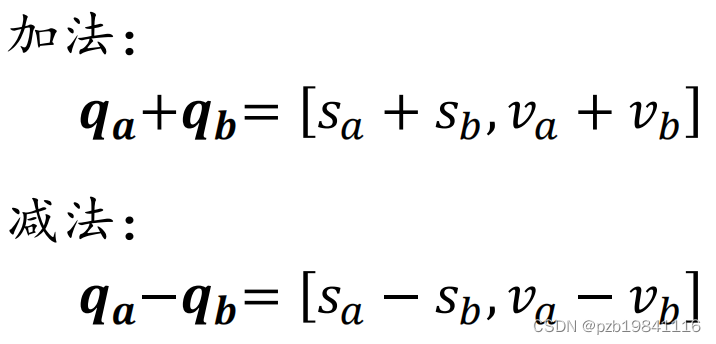

四元数的共轭,
设𝒒𝒂 = [𝑠𝑎, 𝑣𝑎] 𝑞𝑎 = 𝑠𝑎 + 𝑥𝑎𝑖 + 𝑦𝑎𝑗 + 𝑧𝑎k,则
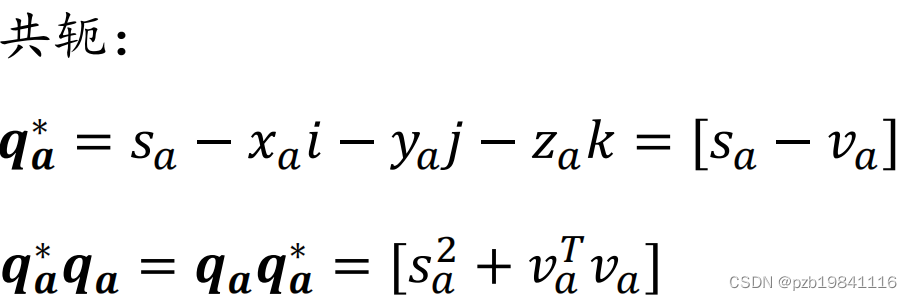
四元数的模长
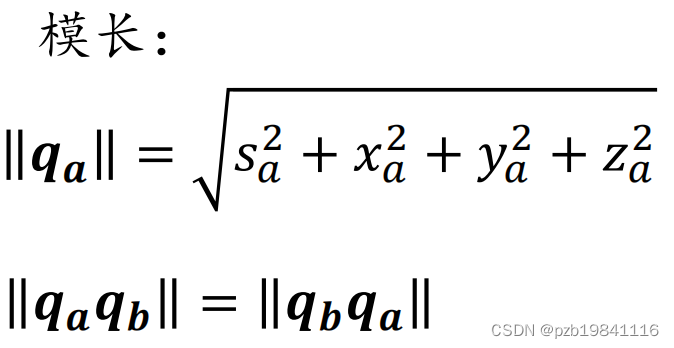
四元数的逆

四元数与旋转之间的计算关系:
三维空间的单位向量𝒏 = [𝑛𝑥, 𝑛𝑦, 𝑛𝑧]',某个旋转是绕单位向量𝒏进行了角度为𝜃的旋转,该旋转的四元数形式为:
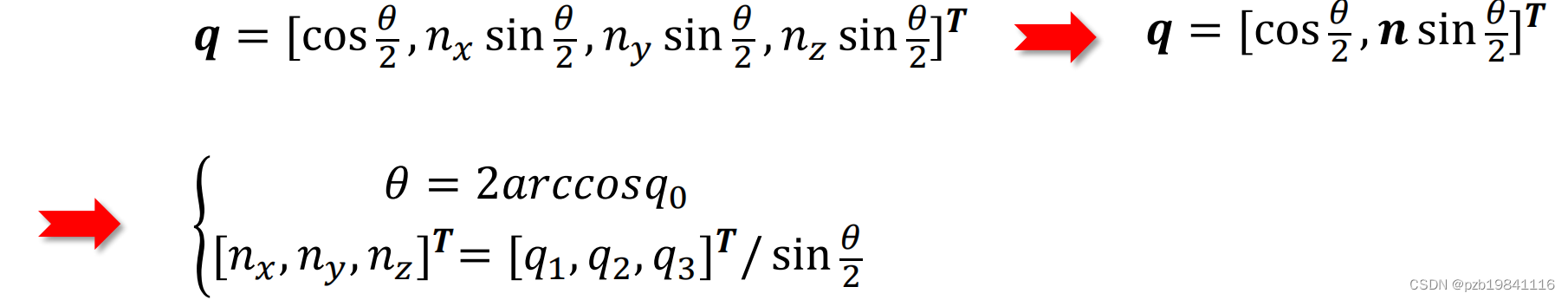
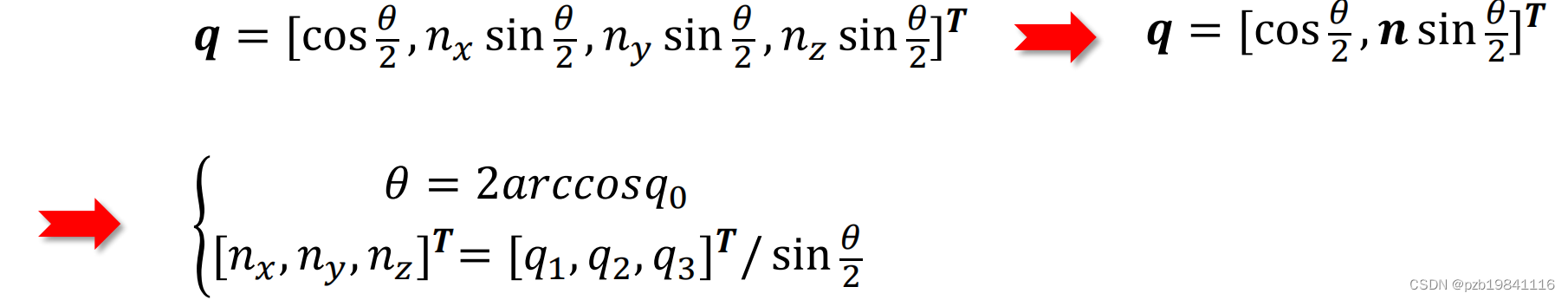
四元素如何用于计算旋转