问题描述：

将面积从最底下一层层叠到最上面可以得到球体积的正确公式

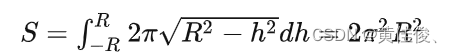
但是将周长从最底下一层层叠到最上面会得到错误结果，错误结果的几何意义是什么？以及是在什么地方积错了？

解答一：

首先， ∫−RR2πR2−h2dh=∫−π2π22πR2cos2θdθ=π2R2 ，不是 2π2R2

其次，在计算表面积的过程中，球上各点处的切平面并不全部与XoY平面垂直，球面的微分的形状是相当于一个圆台侧面，而不是圆柱侧面，故表面积的微分 dS=2πrdl≠2πrdh 。

∫−RR2πR2−h2dlh=Rsinθ,dh=cosθdl=∫−π2π22πR2cosθdθ=4πR2

球的截面图

你这个算法的几何意义跟下图的算法相似，相当于在计算一无限密离散圆柱组成台阶状结构的侧表面积：

但还是有一个不解的地方：

为什么小圆台上下半径可以近似一样而dl与dh不能？

在计算体积时，体积微元取圆台或者圆柱时，圆台和圆柱的体积之差相比于圆柱体积为高价无穷小，在算球体积的积分和时，该差值会趋于0，也就是使用圆台或者圆柱计算结果都会趋于同一个值。
而在计算表面积时，面积微元取圆台或圆柱，二者面积之差相比于圆柱是一个有限量（secθ-1），在计算球面积时，该差值不趋于0，也就是使用圆台或者圆柱计算结果不会趋于同一个值。二者会存在差值。

这在二维平面也是一样的，定积分算面积的时候面积元素可以是梯形也可以是矩形。而算弧长的定积分是∫ds，而不是∫dy。

解答二：

上个图

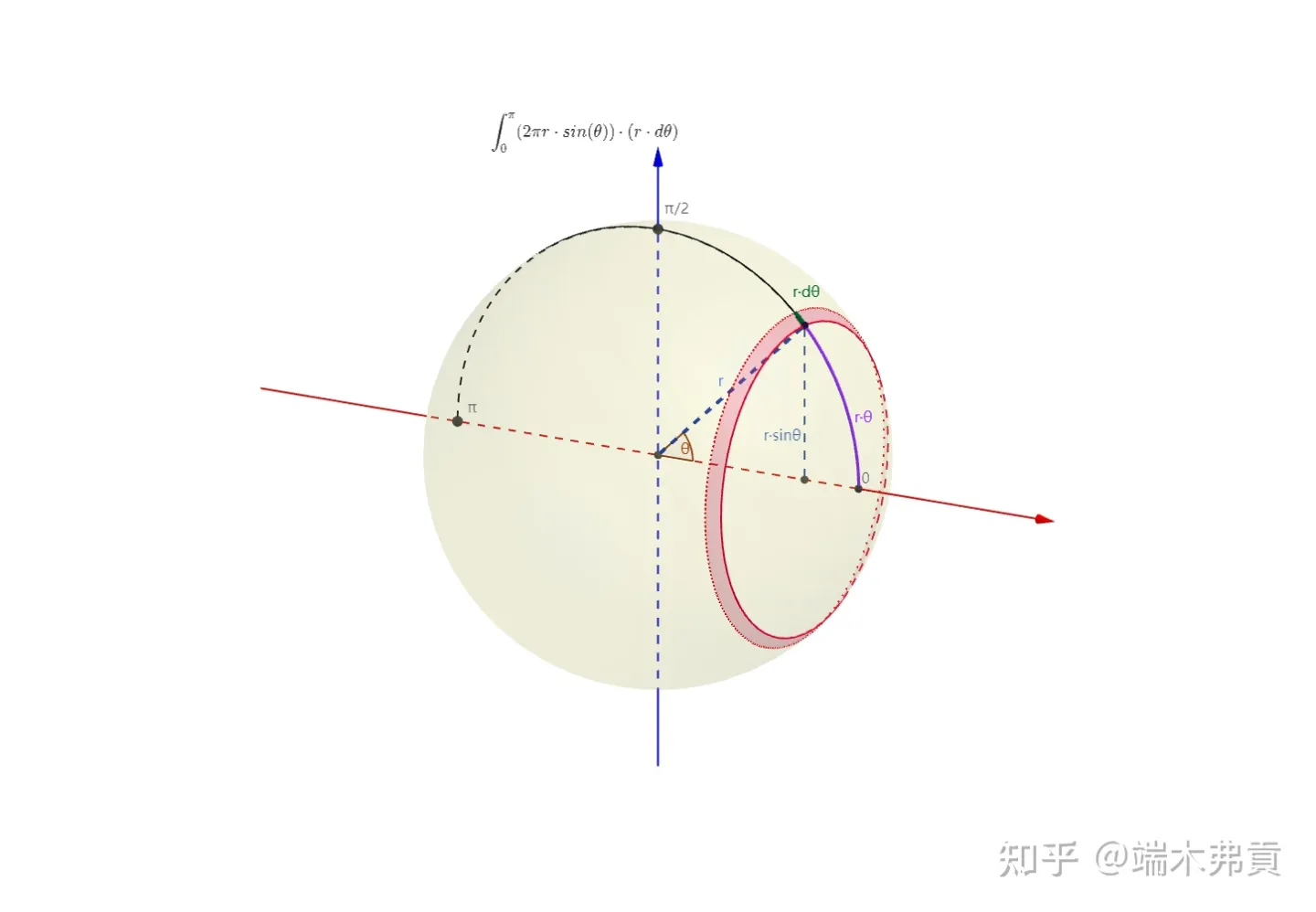
求球体表面积应该是对图中的小红圈做积分。小红圈的上缘周长是 2π⋅r⋅sin(θ) ，圈的侧线的弧长是 r⋅dθ 。整个球体的表面积就是从0到π球面上无数个小圈的面积之和。

∫0π2πr2sinθ⋅dθ=2πr2⋅−(cosπ−cos0)=4πr2

~ ~ ~

体积用面积的积分的说法不正确。体积的就是体积的积分。你题目中的公式里 (πR2−πh2)⋅dh=s(h)⋅dh ，圆片面积×dh 不是体积又是什么？

求球的体积是对极薄的圆饼的体积做积分。同理，求球的表面积就得对圆环或者它外壳上别的一小片什么东西的面积来做积分。dh并不在球的外壳上，也不在我给出的图的圆圈上。所以这个量对求面积而言根本不适用。

解答三：

你这样算出的是柱体的面积，实际上存在一个斜率，比如一个45度角度的椎体z=（x^2+y^2）^1/2，周长乘dz。算出来的是柱体的面积元素，要乘根号2才是面积元素，因此需要使用第一类曲面积分来做，对于斜率不变的圆锥，乘上的系数刚好就是根号2. 

参考：

(2 条消息) 为什么球的表面积不能用周长积分而体积可以用面积积分？ - 知乎 (zhihu.com)