目录
1 概述
2 主要模块说明
2.1 简化电网
2.2 转换器 1
2.3 直流电路
2.4 控制器
2.5 示波器和测量
3 讲解
3.1 参数设置
3.2 SPS 比较
3.3 结果比较
3.4 参考文献
4 Matlab代码实现

1 概述
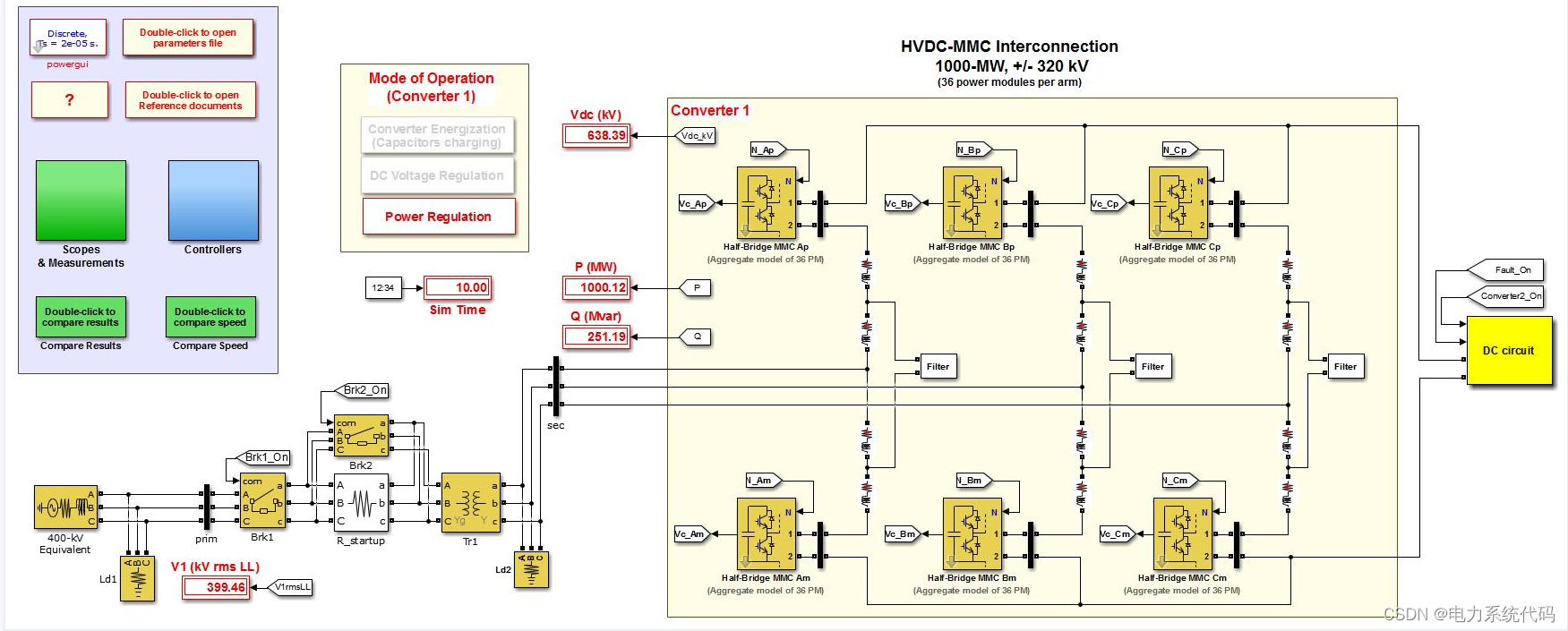
1000 MW HVDC-MMC 互连的 SPS 模型。本文基于模块化多电平转换器 (MMC) 技术的电压源转换器 (VSC) 的高压直流 (HVDC) 互连的 SimPowerSystems (SPS) 模型。 SPS 仿真通过使用聚合 MMC 模型进行了优化。
直流输电线路正成为国家间电力交换和可再生能源(水力发电厂、海上风力发电厂和太阳能发电厂)向电网输送电力的首选方式。其中一些系统目前正在运行,例如Dolwin1项目(海上风电HVDC链路),或计划用于未来的项目,如Northern Pass(加拿大-美国1090-MW直流链路)。
本文案例将说明目前使用的一种典型VSC拓扑:模块化多电平转换器(MMC)技术。在该示例中,MMC转换器使用聚合模型来实现,以模拟每臂 36 个电源模块。通过该聚合模型,可以很好地描述控制系统动力学、变流器谐波和循环电流现象。然而,只有一个虚拟电容器来代表手臂的 36 个电容器,该模型假设所有电源模块的电容器电压是均衡的。聚合模型的运行速度比详细模型要快得多,模型将详细为每个单独的电源模块使用两个开关设备和一个电容器。这种聚合模型也非常适合实时仿真。
模拟本文SPS模型10秒钟,可以观察启动(电容器充电)、电压调节和功率调节期间的互连操作。还提供了该聚合模型与SPS详细模型之间的比较。
2 主要模块说明
2.1 简化电网
电网使用 400 kV、50 Hz 等效电压和两个断路器为转换器 1 供电.
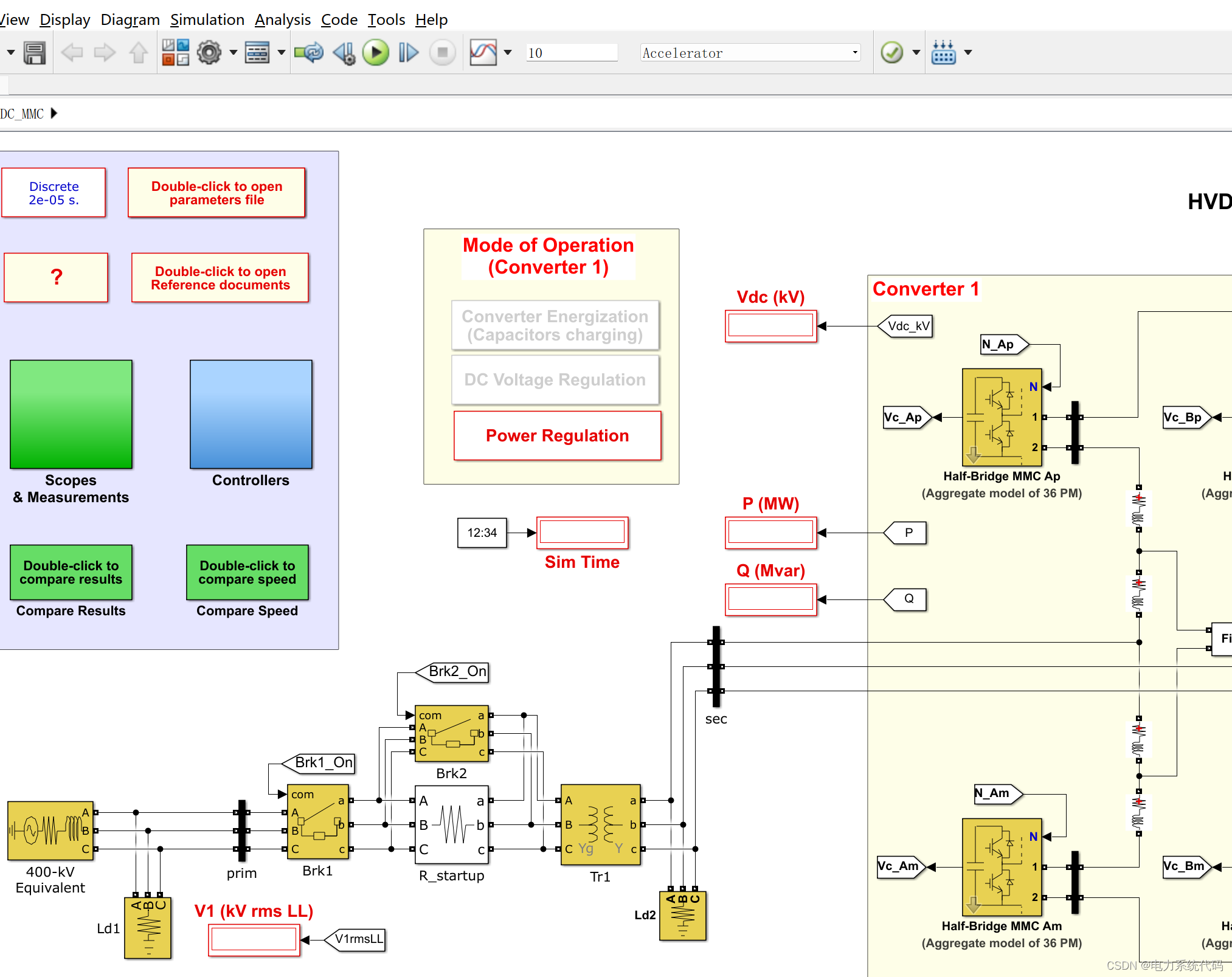
2.2 转换器 1
转换器 1 使用 6 个半桥 MMC 模块实现,每个模块代表 36 个电源模块。此自定义 SPS 模块使用开关功能模型,其中仅使用一个等效模块来表示所有电源模块。控制信号是一个二元向量 [Nin, Nbl],其中 Nin 表示插入模块的数量,Nbl 表示处于阻塞状态的模块数量。输出 Vc(电容器电压)只有一个元素,并给出电容器模块的平均值。
2.3 直流电路
在直流电路子系统中,将会发现电缆的简化模型,以及使用直流电源和理想开关建模的第二个转换器。您还将找到一个开关,用于在电缆上应用故障。
2.4 控制器
控制器子系统包含操作互连所需的各种控制系统。它包括以下子系统:有功和无功功率调节器-直流电压调节器-带前馈的dq电流调节器-PLL和测量子系统-用于控制转换器1(Converter1 )半桥MMC的PWM发电机。在文件夹中还可以找到对转换器1的各种操作模式进行编程的排序器区域。
2.5 示波器和测量
该子系统包含用于在仿真期间观察多个信号的所有示波器。功率和基波电压计算也在子系统中进行。
3 讲解
3.1 参数设置
模拟SPS 模型 10 秒,可以观察启动(电容器充电)、电压调节和功率调节期间的互连操作。运行模型所需的所有参数都可以在:HVDC_MMC_param.m这一子函数中看到。当示例打开时,该文件会在 MATLAB 工作区中自动执行。运行模型并观察到:
%HVDC_MMC_param.m:
% 此模块为SPS模型参数文件: HVDC_MMC.slx
load sound % 操作面板使用的sound.mat
Fnom= 50; % 系统频率 (Hz)
Pnom= 1000e6; %转换器三相额定功率(MVA)
Vnom_prim= 400e3; % 标称初级电压 (V)
Vnom_sec= 333e3; % 标称二次电压 (V)
Nb_PM=36; % 每臂电源模块数
Vnom_dc= 640e3; % 直流标称电压 (V)
C_PM= 1.758e-3; % 电源模块电容器 (F)
%% 能量输入 kJ/MVA
W_kJ_MVA= 0.5 * C_PM * (Vnom_dc/Nb_PM)^2 * Nb_PM * 6 / (Pnom/1e6)/1e3;
Vc0_PM=0; % 电容初始电压 (V)
%% 序列器时序:
Tbrk1_On=0.1; % 断路器1合闸时间(换流器充电量)
Tbrk2_On=1.0; % 断路器 2 的闭合时间(s)(跨启动电阻)
%===========================================================%
Tdeblock=1.5; %转换器解除阻塞时间 (s)
Ton_VDCreg=1.5; % VDC 稳压器开启时间 (s) - VDC 稳压
Tramping_Vdc_ref=2; % 开始时间 Vdc_ref 上升到标称值 (s)
Slope_Vdc_ref=Vnom_dc/5; % 爬坡 (V/s)
%==========================================================%
Ton_PQreg=4; % Preg & Qreg 稳压器开启时间 (s) - PQ 调节
Tramping_Pref=Ton_PQreg+0.2; % 预爬坡开始时间(s)
Slope_Pref=0.5; % 爬坡(V/s)
Tramping_Qref=Ton_PQreg+3.5; % 预爬坡开始时间(s)
Slope_Qref=0.5; % 爬坡(V/s)
%==========================================================%
Ton_Converter2=4; % 转换器 2 等效开启时间 (s)
%%
Tfault= 9999; %直流故障时序( s )
Rfault=1; %直流故障电阻(欧姆)
%% PWM 输出脉冲选择器
pp=0;
for p=1:2:72
pp=pp+1;
SelectPulses1(p)=pp;
SelectPulses1(p+1)=pp+36;
end
%====================================================%
Ts_Power= 20e-6; % SPS仿真时间步长( s )
Ts_Control=40e-6; % 控制系统时间步长(s)
Ts=Ts_Control;
%% 变压器阻抗
Lxfo= 0.12; % 总漏感 (pu)
Rxfo= 0.003; % 总绕组电阻( pu )
Zbase= Vnom_sec^2/Pnom;
Larm_pu=0.15;
Rarm_pu=Larm_pu/100;
Zbase= Vnom_sec^2/Pnom;
Larm=Larm_pu*(Zbase/(2*pi*Fnom));
Rarm=Rarm_pu*Zbase;
w=2*pi*Fnom;
wc2=(2*w)^2;
Cfilter=1/(Larm*wc2); % 2次谐波滤波器的电容值( F )
Rfilter=1/(Cfilter*w)*30; % 2次谐波滤波器的阻值(欧姆)
Topen_Filter=1e6; % 二谐波滤波器的分断器开启时间( s )
%% 控制参数
%======(1)调制器参数======
Fc=Fnom*3.37; %载波频率( Hz )
%======(2)dq 和 Vdc 测量滤波器截止频率:==
Fn_filter=1000;
Zeta_filter=1;
%======(3)有功功率调节器=======
Kp_Preg= 0.5/3; % 比例增益
Ki_Preg= 1.0; % 积分增益
Limits_Preg = [ 1.2, 0.8 ] ; %输出上限/下限 (pu)
%======(4)无功功率调节器======
Kp_Qreg= 0.5/3; % 比例增益
Ki_Qreg= 1.0; % 积分增益
Limits_Qreg = [ 0.25, -0.25 ]; % 输出上限/下限 (pu)
%=====(5)直流稳压器==========
Kp_VDCreg=4; %比例增益
Ki_VDCreg=100; %积分增益
Limits_VDCreg= [ 2.0 -2.0]; % 输出上限/下限 (pu)
%======(6)电流调节器========
Kp_Ireg= 0.6; % 比例增益
Ki_Ireg= 6; % 积分增益
Limits_Ireg= [ 2.0 -2.0]; % 输出上限/下限 (pu)
%=====(7)前馈系数==========
Lff=Larm_pu/2;
Rff= Rarm_pu/2;
%% 电力系统参数
Psc= Pnom*20; % 短路功率 (MVA)
X_R= 7; % X/R ratio
P_Ld1= Psc/30; % 负载(主母线)(MW)
R_startup= 400; % 启动阻力(欧姆)
%=====电缆数据======
R_cable = 0.5; %欧姆
L_cable= 15e-3; % (H)
% 接地( RC)
Rg= 100; % 欧姆
Cg= 50e-9; % (F)
在 0.1 秒时,断路器 1 闭合,转换器 1 通过电阻器通电以降低充电电流。电容器正在充电,并且在 1 秒时,启动电阻器通过闭合断路器 2 短路。
在 1.5 秒时,转换器 1 被解除阻塞并且电压调节器被启用。
在 2 秒时,电压调节器设定点斜升至互连的标称直流工作电压:640 kV (+/-320 kV)。
在 4 秒时,PQ 稳压器启用,转换器 2 开关闭合。
在 4.2 秒时,有功功率调节器设定点斜升至 1pu (1000 MW)。
在 7.5 秒时,无功功率调节器设定点斜升至 0.25pu (250 Mvar)。
如果在工作区中将参数“Tfault”的值设置为 7(实际默认值 =9999)并重新开始仿真,则在 7s 时将在电缆中间施加直流故障。半桥 MMC 将被阻塞,互连将在两个周期后关闭(Brk1 将打开)。
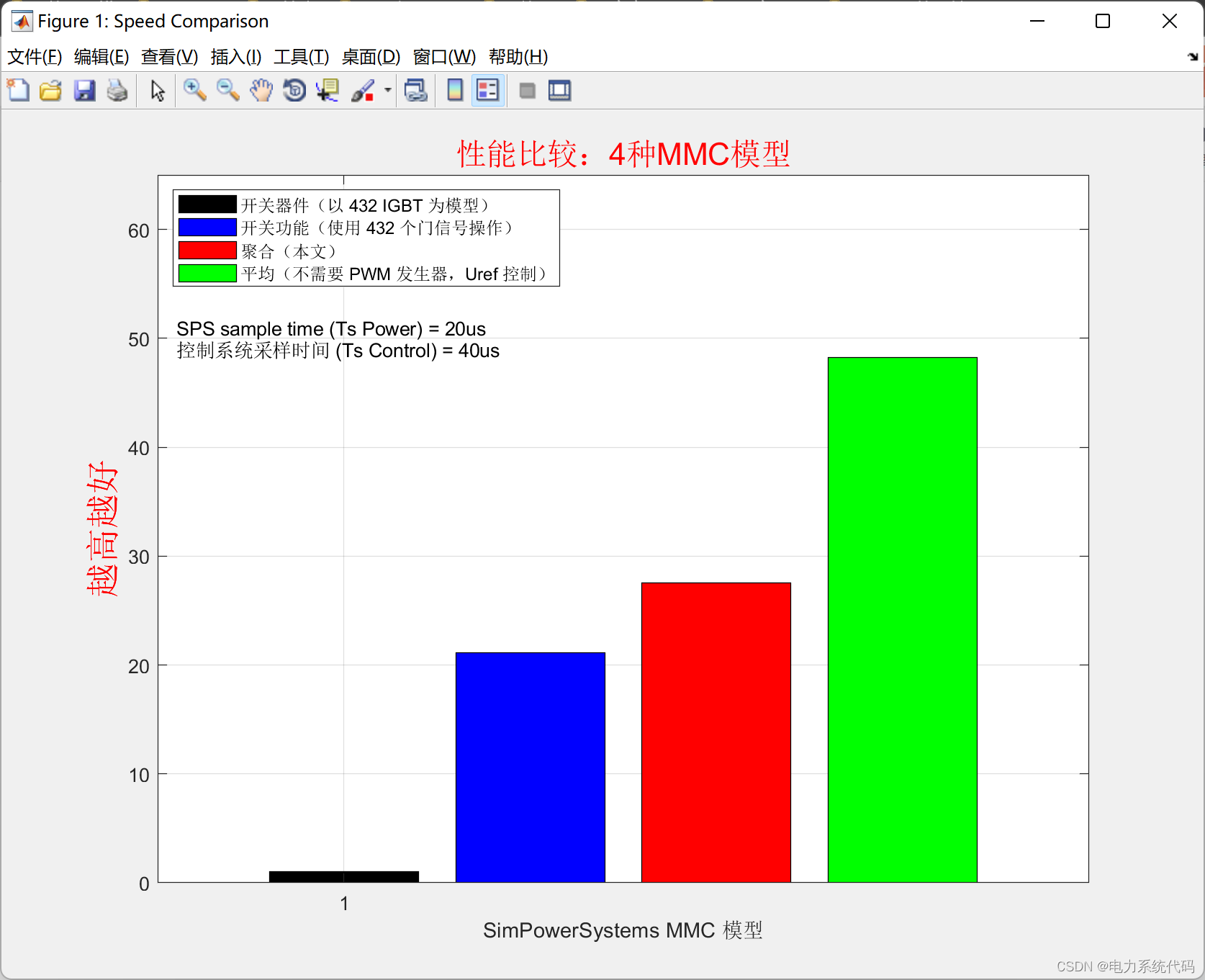
3.2 SPS 比较
要将此模型的结果与包含 432 (2*36*6) 个 IGBT 的详细 SPS 模型进行比较,只需双击比较结果子系统。要将此模型与其他 SPS MMC 模型的仿真速度进行比较,只需双击 Compare Speed 子系统。
close all
%
% Ts_Power=20us & Ts_Control=40us
%
ExecTime(1)=1351; % SwD (s)
ExecTime(2)=64; % SwF (s)
ExecTime(3)=49; % Agg (s)
ExecTime(4)=28; % Avg (s)
%
h1=figure;
set(h1,'Name','Speed Comparison');
ScreenS=get(0,'Screensize');
set(h1,'Position',[ScreenS(3)*0.2 ScreenS(4)*0.16 ScreenS(3)*0.58 ScreenS(4)*0.67])
bar(1,1./(ExecTime(1)/max(ExecTime)),'k')
hold on
bar(2,1./(ExecTime(2)/max(ExecTime)),'b')
bar(3,1./(ExecTime(3)/max(ExecTime)),'r')
bar(4,1./(ExecTime(4)/max(ExecTime)),'g')
ylabel('越高越好','Fontsize',18,'Color','r')
title('性能比较:4种MMC模型','Fontsize',16,'Color','r')
legend('开关器件(以 432 IGBT 为模型)','开关功能(使用 432 个门信号操作)','聚合(本文)', '平均(不需要 PWM 发生器,Uref 控制)','Location','NorthWest')
grid
axis([0 5 0 65])
xlabel('SimPowerSystems MMC 模型')
text(0.1,51,'SPS sample time (Ts Power) = 20us')
text(0.1,49,'控制系统采样时间 (Ts Control) = 40us')
3.3 结果比较

%.......
h1=figure;
set(h1,'Name','DC');
ScreenS=get(0,'Screensize');
set(h1,'Position',[ScreenS(3)*0.01 ScreenS(4)*0.52 ScreenS(3)*0.32 ScreenS(4)*0.37])
subplot(2,1,1)
plot(results.time3,results.signals(1).values*1e-3,'b', ...
results.time3,results.signals(11).values*1e-3,'r')
ylabel('(kV)')
grid
title('Vdc Conv1')
axis([0 10 0 700])
legend('SwD','Agg')
subplot(2,1,2)
plot(results.time3,results.signals(2).values,'b', ...
results.time3,results.signals(12).values,'r')
ylabel('(A)')
xlabel('(s)')
grid
title('Idc Conv1')
legend('SwD','Agg')
axis([0 10 -2000 1000])
%
h1=figure;
set(h1,'Name','PQ');
ScreenS=get(0,'Screensize');
set(h1,'Position',[ScreenS(3)*0.34 ScreenS(4)*0.52 ScreenS(3)*0.32 ScreenS(4)*0.37])
subplot(2,1,1)
plot(results.time2,results.signals(3).values,'b', ...
results.time2,results.signals(13).values,'r')
ylabel('(MW)')
grid
title('有功功率')
axis([0 10 -500 1500])
legend('SwD','Agg','Location','southeast')
subplot(2,1,2)
plot(results.time2,results.signals(4).values,'b', ...
results.time2,results.signals(14).values,'r')
ylabel('(Mvar)')
xlabel('(s)')
grid
title('无功功率')
axis([0 10 -300 300])
legend('SwD','Agg','Location','southeast')
%
%
h1=figure;
set(h1,'Name','Iprim');
ScreenS=get(0,'Screensize');
set(h1,'Position',[ScreenS(3)*0.67 ScreenS(4)*0.52 ScreenS(3)*0.32 ScreenS(4)*0.37])
plot(results.time1(1:25000),results.signals(5).values(1:25000),'b')
hold on
plot(results.time1(1:25000),results.signals(15).values(1:25000),'r')
ylabel('(A)')
xlabel('(s)')
grid
title('一次电流, A相')
axis([0.35 0.45 -250 250])
text(0.38,225,'(during capacitors energization)')
legend('SwD','Agg','Location','southeast')
%
h1=figure;
set(h1,'Name','Vcap');
ScreenS=get(0,'Screensize');
set(h1,'Position',[ScreenS(3)*0.01 ScreenS(4)*0.06 ScreenS(3)*0.32 ScreenS(4)*0.37])
subplot(2,2,1)
plot(results.time1(225000:250000),results.signals(6).values)
ylabel('(V)')
axis([9.9 9.98 16000 20000])
grid
title('Vcap 4 模块; SwD')
subplot(2,2,2)
plot(results.time1(225000:250000),results.signals(16).values,'r')
axis([9.9 9.98 16000 20000])
ylabel('(V)')
grid
title('Vcap 平均值: Agg')
subplot(2,2,[3:4])
plot(results.time1(225000:250000),results.signals(7).values,'b', ...
results.time1(225000:250000),results.signals(17).values,'r')
ylabel('(V)')
axis([9.9 9.98 16000 20000])
xlabel('(s)')
grid
title('电容器平均电压,上臂 phA')
legend('SwD','Agg','Location','northeast')
%
h1=figure;
set(h1,'Name','Iarm');
ScreenS=get(0,'Screensize');
set(h1,'Position',[ScreenS(3)*0.34 ScreenS(4)*0.06 ScreenS(3)*0.32 ScreenS(4)*0.37])
plot(results.time1(225000:250000),results.signals(8).values,'b', ...
results.time1(225000:250000),results.signals(18).values,'r')
ylabel('(A)')
xlabel('(s)')
grid
title('臂, 上臂, A相')
axis([9.9 10.0 -2000 2000])
legend('SwD','Agg','Location','southeast')
%
h1=figure;
set(h1,'Name','Iprim');
ScreenS=get(0,'Screensize');
set(h1,'Position',[ScreenS(3)*0.67 ScreenS(4)*0.06 ScreenS(3)*0.32 ScreenS(4)*0.37])
plot(results.time1(225000:250000),results.signals(5).values(225000:250000),'b', ...
results.time1(225000:250000),results.signals(15).values(225000:250000),'r')
ylabel('(A)')
xlabel('(s)')
grid
title('A相一次电流')
axis([9.9 10.0 -2500 2500])
text(9.935,2300,'(in steady-state)')
legend('SwD','Agg','Location','southeast')
% 需要准备:
Simulink
SimPowerSystems
Simscape
3.4 参考文献
[1]VSC-HVDC Transmission with Cascaded Two-Level Converters
Bjorn Jacobson, Patrik Karlsson, Gunnar Asplund, Lennart Harnefors, Tomas Jonsson
ABB,Sweden
CIGRE 2010 B4-110
[2]Setup and Performance of the Real-Time Simulator used for Hardware-in-Loop-Tests of a
VSC-Based HVDC scheme for Offshore Applications.
O. Venjakob, S. Kubera, R. Hibberts-Caswell, P.A. Forsyth, T.L. Maguire
Siemens, Germany & RTDS Technologies, Canada
Paper submitted to the International Conference on Power Systems Transients (IPST2013) in
Vancouver, Canada July 18-20, 2013.
4 Matlab完整代码实现
回复:基于转换器 (MMC) 技术和电压源转换器 (VSC) 的高压直流 (HVDC) 模型