Problem - D - Codeforces

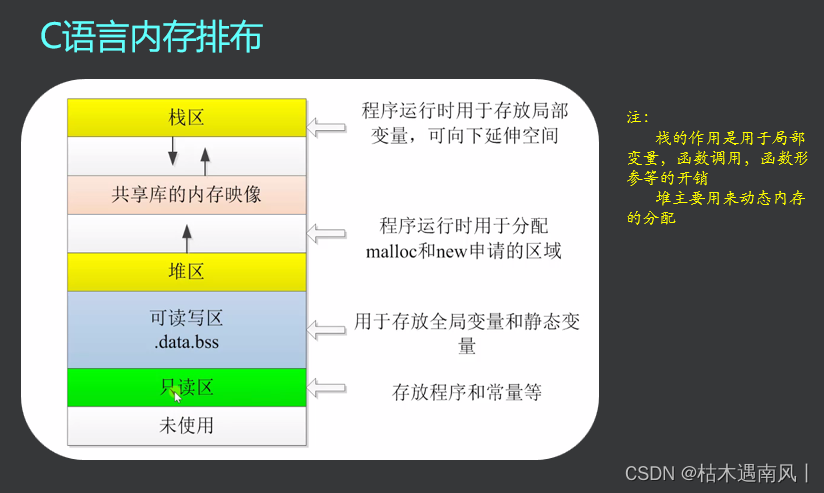
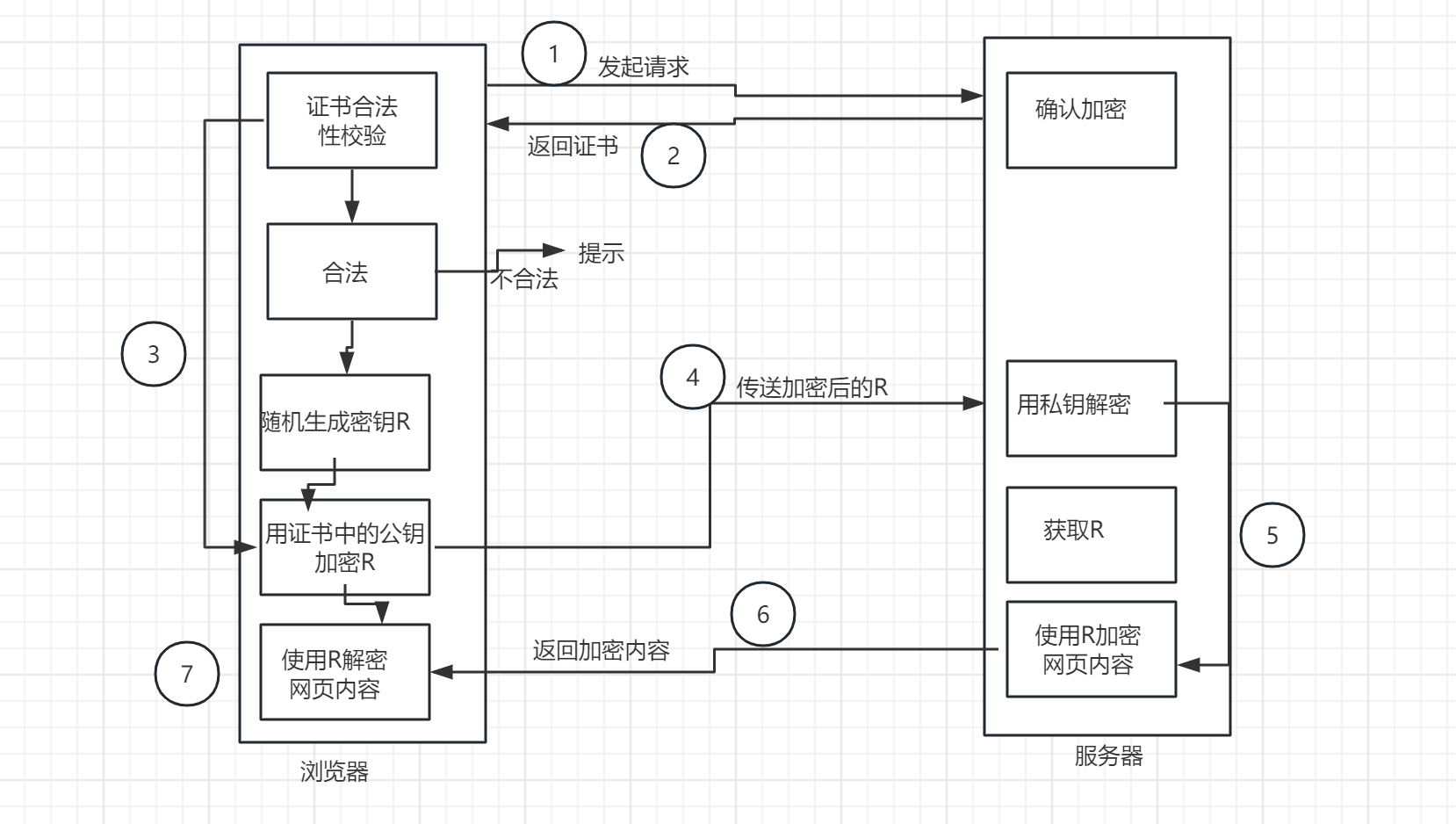
题目大意：有一个隐藏的排列，给出其长度n，每次可以询问一个[l,r]区间内有多少逆序对，费用为，要求在总费用不超过的情况下输出最大值的下标

2<=n<=2000

思路：首先可以发现如果我们想要知道两个数a[i],a[j]的大小关系，只要知道[i,j]的逆序对数量和[i,j-1]的逆序对数量，如果两者相等，说明a[j]没有提供逆序对也就是a[j]>a[i]，反之a[i]>a[j]。

显然这是唯一可以确定大小关系的策略，考虑如何用最少的费用得到答案，首先我们每相邻两个元素询问一下，有1个就说明左边的比右边大，于是记录其中更大的数，这样就得到了每两个数中最大的数，下一轮在每相邻两个数询问一下，这样就得到了每4个数中最大的数，用滚动数组维护每轮循环，直到数组中只剩下唯一的数是，该数即为n个数中的最大数，总费用不会算，但可以确定是花费最小的策略

//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
int n;
void solve()
{
	cin >> n;
	vector<int>temp;
	for (int i = 1; i <= n; i++)
	{//先将所有数存入数组中
		temp.push_back(i);
	}
	while (1)
	{
		if (temp.size() == 1)
		{//最后剩下的一个数就是答案
			cout << "! " << temp[0] << endl;
			cout.flush();
			return;
		}
		vector<int>temp2;//滚动数组
		for (int i = 0; i < temp.size() - 1; i += 2)
		{//每两个数询问一下
			int ret1, ret2;
			if (temp[i] + 1 == temp[i + 1])
			{//如果两个数相邻，只需要问一次就能确定大小关系
				cout << "? " << temp[i] << " " << temp[i + 1] << endl;
				cout.flush();
				cin >> ret1;
				if (ret1)
				{
					temp2.push_back(temp[i]);
				}
				else
				{
					temp2.push_back(temp[i + 1]);
				}
				continue;
			}
			cout << "? " << temp[i] << " " << temp[i + 1] << endl;
			cout.flush();
			cin >> ret1;
			cout << "? " << temp[i] << " " << temp[i + 1] - 1 << endl;
			cout.flush();
			cin >> ret2;
			if (ret1 == ret2)
			{//[l,r]=[l,r-1]，说明a[l]<a[r]，存更大的数
				temp2.push_back(temp[i + 1]);
			}
			else
			{
				temp2.push_back(temp[i]);
			}
		}
		if (temp.size() & 1)
		{//最后一个数没人和他配对，直接存进去
			temp2.push_back(temp.back());
		}
		temp.clear();
		for (int i = 0; i < temp2.size(); i++)
		{//滚一下数组
			temp.push_back(temp2[i]);
		}
	}
	return;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin >> t;
	while (t--)
	{
		solve();
	}
}