凸包模板题：

在平面上能包含所有给定点的最小凸多边形叫做凸包。

实际上可以理解为用一个橡皮筋包含住所有给定点的形态。

凸包用最小的周长围住了给定的所有点。如果一个凹多边形围住了所有的点，它的周长一定不是最小，如下图。根据三角不等式，凸多边形在周长上一定是最优的

 图来自oiwiki

过程

首先把所有点以横坐标为第一关键字，纵坐标为第二关键字排序。

显然排序后最小的元素和最大的元素一定在凸包上。而且因为是凸多边形，我们如果从一个点出发逆时针走，轨迹总是「左拐」的，一旦出现右拐，就说明这一段不在凸包上。因此我们可以用一个单调栈来维护上下凸壳。

因为从左向右看，上下凸壳所旋转的方向不同，为了让单调栈起作用，我们首先 升序枚举 求出下凸壳，然后 降序 求出上凸壳。

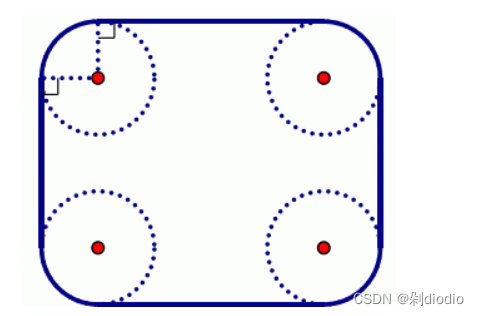
这道题很明显就是求一个凸包，但还有一个限制条件：就是距离要超过 m ，那我们加上一个圆的的距离就行 具体看下图：

#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;

typedef pair<double, double> PDD;

const int N = 100010;
const double eps = 1e-8 ,PI = acos(-1.0);

int n, m,stk[N], top;
bool st[N];
double t;
PDD q[N];

double get_dist(PDD a, PDD b)
{
    double dx = a.x - b.x;
    double dy = a.y - b.y;
    return sqrt(dx * dx + dy * dy);
}

int sign(double x)
{
    if (fabs(x) < eps) return 0;
    return x < 0 ? -1 : 1;
}

double cross(double x1, double y1, double x2, double y2)
{
    return x1 * y2 - x2 * y1;
}

double area(PDD a, PDD b, PDD c)
{
    return cross (b.x - a.x, b.y - a.y, c.x - a.x, c.y - a.y);
}

double andrew()
{
    sort(q, q + n);
    memset(st,0,sizeof st);
    memset(stk,0,sizeof stk);
    top = 0;
    t = 0;
    for (int i = 0; i < n ; i++)
    {
        while (top >= 2 && (t = sign(area(q[stk[top - 1]], q[stk[top]], q[i]))) >= 0)
        {
            // 处于凸包边界上的点不能再用
            if (t > 0) st[stk[top]] = false;
            -- top;
        }
        stk[++top] = i;
        st[i] = true;
    }
    st[0] = false;
    for (int i = n - 1; i >= 0; i--)
    {
        if (st[i]) continue;
        while (top >= 2 && sign(area(q[stk[top - 1]], q[stk[top]], q[i])) >= 0)
            -- top;
        stk[++top] = i;
    }

    double res =  PI * m * 2 ;
    for (int i = 2; i <= top; i++)
        res += get_dist(q[stk[i - 1]], q[stk[i]]);

    return res;
}

signed main() {

    while (cin >> n >> m) {
        for (int i = 0; i < n; i++) cin >> q[i].x >> q[i].y;
        if (n == 2) { //对于 2 个点的情况很明显构不成凸多边形，所以要特判！
            double res = m * 2 * PI + get_dist(q[0], q[1]) * 2;
            printf("%.0lf\n", res);
        } else {
            printf("%.0lf\n", andrew());
        }
    }
    return 0;
}