代码部分前有一千六百字了

P1941 [NOIP2014 提高组] 飞扬的小鸟 考察对背包 dp 算法过程理解的透彻性。过程透彻性也是解决所有问题的关键（建立在算法已学的基础上）。

$n,m$ 的范围足够我们 $O(nm)$ 的遍历整个地图。设 $f_{i,j}$ 表示到 $(i,j)$ 格子时的最小点击数，考虑转移，共两种情况，分别是由前一个格子下移（即不动）或上移 $x$ 次得到的。由于下移操作只有选或不选两种情况，我们可以把下移操作当作 01 背包来转移，即 $f_{i}j=\min (f_{i,j},f_{i-1,j+down[i-1]})$。

上移操作可以进行多次，如果对于每个格点上移操作分别进行 $0$ 至 $m/up[i]$ 次的转移显然会超时，观察发现，单独对 $f_{i,j}$ 进行上移操作的转移时，$f_{i,j}=\min (f_{i,j},f_{i-1,j-up[i-1]\times x})$ 与 $f_{i,j}=\min (f_{i,j},\min (f_{i-1,j-up[i-1]},f_{i,j-up[i-1]}))$ 的本质相同，而这正是完全背包算法过程的关键。

既然本质相同，那么转移方法便与完全背包保持一致性。注意到由于每个点不能同时选择上移和下移，而上移操作的转移用到了 $f_{i,j-up[i-1]}$ 即当前列某一位置的值，由上可知在对上移操作的转移中，使用到的 $f_{i,j-up[i-1]}$ 不能包含下移操作的更新，即使用到的 $f_{i,j-up[i-1]}$ 必须只包含上移操作的更新状态。

那么这里有两种方法，一种是将两次操作的转移分开，因为下移操作的转移需要用到的 $f_{i-1,j-1+down[i-1]}$ 为前一列的值，且两种操作的转移都不会干扰前一列的值，所以可以先更新上移操作，再更新下移操作。

另一种是新增一维状态，设 $f_{i,j,0/1}$ 表示 $(i,j)$ 由上一列下移 /上移得到。思维量很小，但显然没有第一种方法简便。（我用的就是这种（

注意上移时高度到了 $m$ 将无法再上升，但和 $0$ 处不同，冲到 $m$ 高度不会使游戏结束。
所以转移时高度超过 $m$ 的部分要参与 dp ，并转移至 $m$ 那。

最后考虑柱子和是否能通关的判断。对于柱子，首先记得排序，可以在转移完毕之后将柱子所在处的 $f$ 值再赋为 $\inf$，也可以干脆在转移过程前标记，转移时就特判掉并跳过，当然也不可以不这么麻烦（猜对了我就这么敲的，调半天不对（

通关判断就很简单了，转移完扫一遍当前列有没有解，到不了就退出，通过柱子数为当前柱子编号 $-1$，当前列过不了肯定说明有柱子（因为无论如何都可以一直按屏幕保持在 $m$ 高度），当前柱子过不了自然过了的柱子就是编号 $-1$ 了。

时间复杂度 $O(nm)$。
空间复杂度 $O(nm)$，可以滚掉一维，故为 $O(m)$。

#include<bits/stdc++.h>
using namespace std;
int n,m,k,up[10005],down[10005],f[2][2005][2];
struct qh{
	int p,l,h;
	bool operator < (const qh &T)const {return p<T.p;}
}a[10005];
inline int Rd(){
	int s=0,w=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if(ch=='-') w=-1;ch=getchar();}
	while (ch>='0'&&ch<='9') s=(s<<1)+(s<<3)+ch-'0',ch=getchar();
	return s*w;
}
int main(){
	n=Rd();m=Rd();k=Rd();
	for(int i=0;i<n;i++) up[i]=Rd(),down[i]=Rd();
	for(int i=1;i<=k;i++) a[i]=(qh){Rd(),Rd(),Rd()};
	sort(a+1,a+k+1);
//	for(int i=1;i<=k;i++) printf("%d %d %d\n",a[i].p,a[i].l,a[i].h);
	int z=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m*2;j++) f[i%2][j][0]=f[i%2][j][1]=1e9;
		for(int j=1;j<=m*2;j++){
			if(j+down[i-1]<=m) f[i%2][j][0]=min(f[(i-1)%2][j+down[i-1]][0],f[(i-1)%2][j+down[i-1]][1]);
			if(j-up[i-1]>0) f[i%2][j][1]=min(f[i%2][j-up[i-1]][1],min(f[(i-1)%2][j-up[i-1]][0],f[(i-1)%2][j-up[i-1]][1]))+1;
		}
		for(int j=m+1;j<=m*2;j++) f[i%2][m][1]=min(f[i%2][m][1],f[i%2][j][1]);
		if(a[z+1].p==i){
			z++;
			for(int j=1;j<=a[z].l;j++) f[i%2][j][0]=f[i%2][j][1]=1e9;
			for(int j=a[z].h;j<=m*2;j++) f[i%2][j][0]=f[i%2][j][1]=1e9;
//			printf("%d %d %d %d\n",z,a[z].p,a[z].l,a[z].h);
		}
		int mn=1e9;
		for(int j=1;j<=m;j++) mn=min(mn,min(f[i%2][j][0],f[i%2][j][1]));
//		for(int j=1;j<=m;j++) printf("%d %d ",f[i%2][j][0],f[i%2][j][1]);puts("");
		if(mn==1e9) return printf("0\n%d",z-1),0;
	}
	int ans=1e9;
	for(int i=1;i<=m;i++) ans=min(ans,min(f[n%2][i][0],f[n%2][i][1]));
	printf("1\n%d",ans);
	return 0;
}
/*
start coding:09:44 
finish debiuging:11:05
*/

---

附上题目：

[NOIP2014 提高组] 飞扬的小鸟

题目描述

Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度，让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话，便宣告失败。

为了简化问题，我们对游戏规则进行了简化和改编:

游戏界面是一个长为 $n$，高为 $m$ 的二维平面，其中有 $k$ 个管道（忽略管道的宽度）。

小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发，到达游戏界面最右边时，游戏完成。

小鸟每个单位时间沿横坐标方向右移的距离为 $1$，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度 $x$，每个单位时间可以点击多次，效果叠加；如果不点击屏幕，小鸟就会下降一定高度 $y$。小鸟位于横坐标方向不同位置时，上升的高度 $x$ 和下降的高度 $y$ 可能互不相同。

小鸟高度等于 $0$ 或者小鸟碰到管道时，游戏失败。小鸟高度为 $m$ 时，无法再上升。

现在,请你判断是否可以完成游戏。如果可以，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。

输入格式

第 $1$ 行有 $3$ 个整数 $n,m,k$，分别表示游戏界面的长度，高度和水管的数量，每两个整数之间用一个空格隔开；

接下来的 $n$ 行，每行 $2$ 个用一个空格隔开的整数 $x$ 和 $y$，依次表示在横坐标位置 $0\sim n-1$ 上玩家点击屏幕后，小鸟在下一位置上升的高度 $x$，以及在这个位置上玩家不点击屏幕时，小鸟在下一位置下降的高度 $y$。

接下来 $k$ 行，每行 $3$ 个整数 $p,l,h$，每两个整数之间用一个空格隔开。每行表示一个管道，其中 $p$ 表示管道的横坐标，$l$ 表示此管道缝隙的下边沿高度，$h$ 表示管道缝隙上边沿的高度（输入数据保证 $p$ 各不相同，但不保证按照大小顺序给出）。

输出格式

共两行。

第一行，包含一个整数，如果可以成功完成游戏，则输出 $1$，否则输出 $0$。

第二行，包含一个整数，如果第一行为 $1$，则输出成功完成游戏需要最少点击屏幕数，否则，输出小鸟最多可以通过多少个管道缝隙。

样例 #1

样例输入 #1

10 10 6 
3 9  
9 9  
1 2  
1 3  
1 2  
1 1  
2 1  
2 1  
1 6  
2 2  
1 2 7 
5 1 5 
6 3 5 
7 5 8 
8 7 9 
9 1 3

样例输出 #1

1
6

样例 #2

样例输入 #2

10 10 4 
1 2  
3 1  
2 2  
1 8  
1 8  
3 2  
2 1  
2 1  
2 2  
1 2  
1 0 2 
6 7 9 
9 1 4 
3 8 10

样例输出 #2

0
3

提示

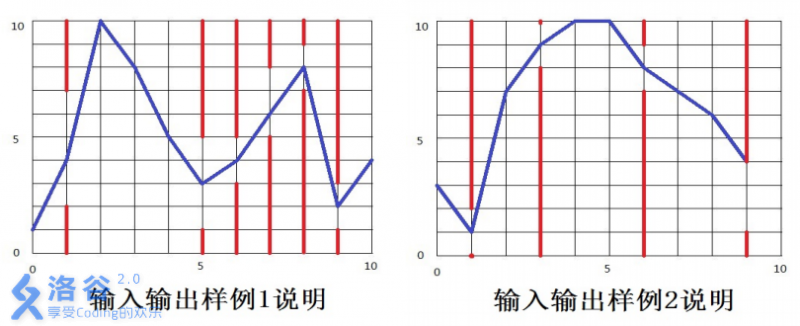
【输入输出样例说明】

如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

【数据范围】

对于 $30\%$ 的数据：$5\le n\le 10,5\le m\le 10,k=0$，保证存在一组最优解使得同一单位时间最多点击屏幕 $3$ 次；

对于 $50\%$ 的数据：$5\le n\le 20,5\le m\le 10$，保证存在一组最优解使得同一单位时间最多点击屏幕 $3$ 次；

对于 $70\%$ 的数据：$5\le n\le 1000,5\le m\le 100$；

对于 $100\%$ 的数据：$5\le n\le 10000$，$5\le m\le 1000$，$0\le k<n$，$0<x,y<m$，$0<p<n$，$0\le l<h\le m$， $l+1<h$。

---

start writing:19:00
finish the work:20:33