---

简介

树状数组是一种树形数据结构，支持在 $O(\log n)$ 的时间复杂度内进行 单点修改 和 查询前缀和 的操作。

• 优点：常数小，码量小，操作灵活简便。
• 缺点：只能用来维护具有 结合律 且 可差分 的信息。例如：区间和、积等，而不能维护区间最大（最小）值。

引入

现在想要让你实现两个操作：

1. 单点修改
2. 查询 $[1,x]$ 的和

在没有学过树状数组的时候你会怎么做？

1. 直接暴力

单点修改虽然方便，但前缀和是 $O(n)$ 复杂度。

2. 维护前缀和数组

这样做虽然查询是 $O(1)$ 了，但单点修改又是 $O(n)$。

总结

• 暴力
  • 修改：$O(1)$
  • 查询：$O(n)$
• 前缀和
  • 修改：$O(n)$
  • 查询：$O(1)$

那么我们不妨考虑一个折中的办法，两种操作都是 $O(\log n)$ 的复杂度。

---

定义

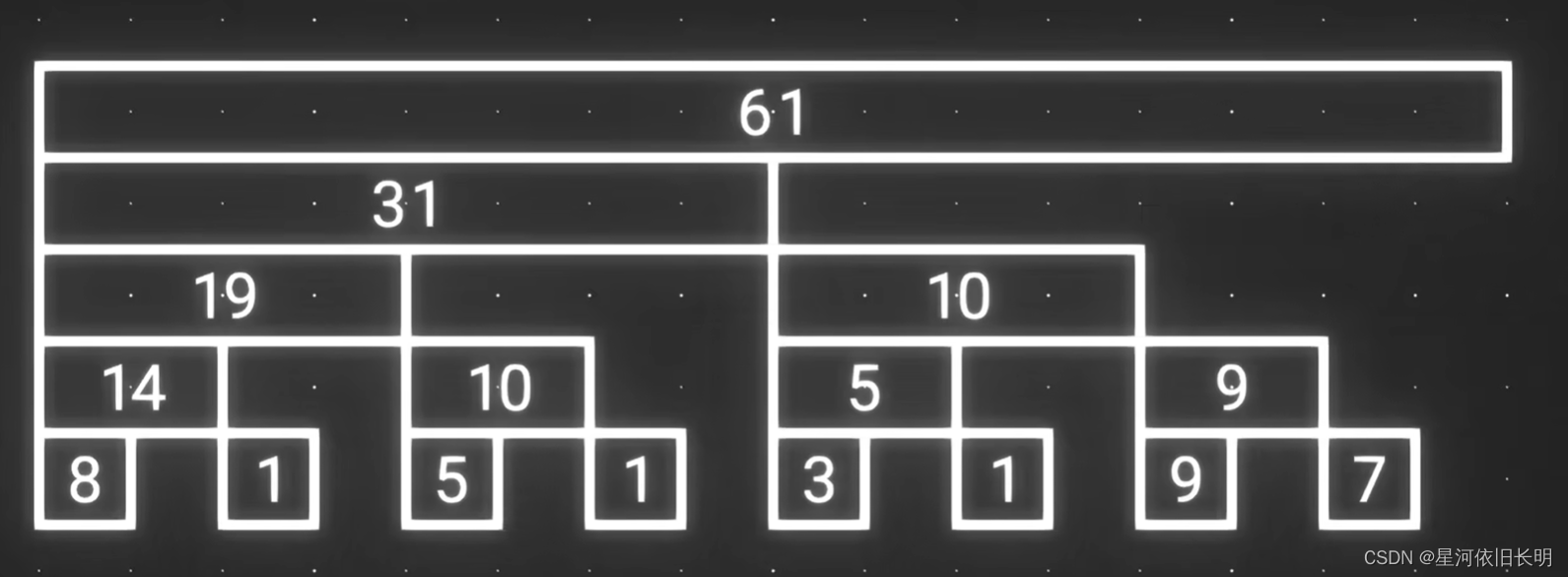
注：这里的数值表示的是该区间所有元素的和，也就是这个节点左下方的所有直接相关节点的总和。
例如：权值为 $31$ 的节点表示的是权值分别为 $19,10,1$ 的节点以及原数组中下表为 $8$ 的元素之和。

显然，我们能求出原数组为

$$[8,6,1,4,5,5,1,1,3,2,1,4,9,0,7,4]$$

这里插一句话：树状数组可以近似看成线段树去掉所有右儿子构成的树。

---

前置知识：$\mathrm{lowbit}$ 操作

一个二进制数的 $\mathrm{lowbit}$ 值就是这个数末尾第一个非零的位置的权值。

举个例子：$100010_{(2)}$

这个数的 $\mathrm{lowbit}$ 值是 $10_{(2)}$，即 $2_{(10)}$。

那么这个怎么用代码实现呢？

void lowbit(int x)
{
	return x & -x;
}

什么？你问为什么这么简单？？

$这都不知道，赶紧退役吧hh$

这里涉及到补码的概念。

一个二进制数的补码就是其二进制上的每一位都按位取反之后再 $+1$。

还是那个数：$100010_{(2)}$

先按位取反：$011101_{(2)}$

再加一：$11110_{(2)}$

我们惊奇地发现，它们的后两位竟然是一样的！！！

我们把它们进行按位与运算 &，得到的结果是 $10_{(2)}$，即 $2_{(10)}$，与我们刚才进行手动 $\mathrm{lowbit}$ 运算的结果相同。

在计算机的运算过程中，由于是按照补码储存的，所以我们需要的 ~x + 1 就可以写成 -x。

因此 $\mathrm{lowbit}$ 才能写成 x & -x。

---

区间的表示方法

对于每个标号为 $x$ 的节点，我们发现它父节点的标号为 $x+\text{lowbit}x$。

而每个区间的范围都是 $(x-\text{lowbit}(x),x]$。

---

操作

单点修改

对于每个被修改的点，我们需要找到它的所有祖先节点并都进行修改操作。

考虑到它们标号的关系，我们只要每次加一个 $\text{lowbit(x)}$ 就能找到所有祖先节点了。

代码：

void add(int x, int c) // 将第 x 个数加 c
{
	for (int i = x; i <= n; i += lowbit(i))
		tr[i] += c;
}

---

前缀和查询

实践是检验真理的唯一标准。

经过我们的实践，找到该节点前面的所有节点，只需要每次减 $\text{lowbit(x)}$ 即可。

代码：

void query(int x) // 查询 1~x 的和
{
	int res = 0;
	for (int i = x; i; i -= lowbit(i))
		res += tr[i];
	return res;
}

---

任意区间查询

我们都知道前缀和的性质。

$$\sum _{i=l}^r{w}_i=\sum _{i=1}^r{w}_i-\sum _{i=1}^{l-1}{w}_i$$

代码：

void Query(int l, int r) // 查询 [l,r] 的和
{
	return query(r) - query(l - 1);
}

---

例题1: 单点修改，区间查询

原题链接：P3374 【模板】树状数组 1

操作和上面的相同，直接上代码：

#include <iostream>

using namespace std;

const int N = 500010;

int n, m;
int a[N];
int tr[N];

int lowbit(int x)
{
	return x & -x;
}

void add(int x, int c)
{
	for (int i = x; i <= n; i += lowbit(i))
		tr[i] += c;
}

int sum(int x)
{
	int res = 0;
	for (int i = x; i; i -= lowbit(i))
		res += tr[i];
	return res;
}

int main()
{
	int op, x, y;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++ )
		scanf("%d", &a[i]), add(i, a[i]);
	
	while (m -- )
	{
		scanf("%d%d%d", &op, &x, &y);
		if (op == 1) add(x, y);
		else printf("%d\n", sum(y) - sum(x - 1));
	}
	
	return 0;
}

---

例题2: 区间修改，单点查询

原题链接：P3368 【模板】树状数组 2

同一道题，思路已经在昨天的 【笔记】线段树 里面讲了，无非是维护一个差分数组。

代码：

#include <iostream>

using namespace std;

const int N = 500010;

int n, m;
int a[N], b[N];
int tr[N];

int lb(int x)
{
	return x & -x;
}

void add(int x, int v)
{
	for (int i = x; i <= n; i += lb(i))
		tr[i] += v;
}

int q(int x)
{
	int res = 0;
	for (int i = x; i; i -= lb(i))
		res += tr[i];
	return res;
}

int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i ++ )
		cin >> a[i], b[i] = a[i] - a[i - 1], add(i, b[i]);
	
	while (m -- )
	{
		int op, x, y, k;
		cin >> op >> x;
		if (op == 1)
		{
			cin >> y >> k;
			add(x, k), add(y + 1, -k);
		}
		else cout << q(x) << endl;
	}
}

---

例题3: 区间修改，区间查询

原题链接：P3372 【模板】线段树 1

不要说我用线段树的题练习树状数组，我找不到树状数组的模板题才用的这个

考虑用树状数组 tr[] 维护差分数组

则求原数组的前缀和

$$\{\begin{array}{cccccccccc}{a}_1& =& d_1& & & & & & & \\ a_2& =& d_1& +& d_2& & & & & \\ a_3& =& d_1& +& d_2& +& d_3& & & \\ .& .& .& .& .& .& & & & \\ a_n& =& d_1& +& d_2& +& ...& +& d_n& \end{array}$$

$$s_i=\sum _{i=1}^n{a}_i=\{\begin{array}{cccccccccc}{d}_1& & & & & & & & & \\ d_1& +& d_2& & & & & & & \\ d_1& +& d_2& +& d_3& & & & & \\ .& .& .& .& .& .& & & & \\ d_1& +& d_2& +& ...& +& d_n& & & \end{array}$$

我们考虑把后面的矩阵补全：

则

$$s_i=(n+1)\times \sum _{i=1}^n{d}_i-\sum _{i=1}^n(i\times d_i)$$

所以我们需要两个树状数组，tr1[] 维护差分数组，tr2[] 维护 $i\times d_i$

代码：

#include <iostream>

using namespace std;

typedef long long LL;

const LL N = 1000010;

LL n, m;
LL a[N];
LL t1[N], t2[N];

inline LL lowbit(LL x)
{
    return x & -x;
}

inline void add(LL t[], LL x, LL c)
{
    for (LL i = x; i <= n; i += lowbit(i))
        t[i] += c;
}

inline LL sum(LL t[], LL x)
{
    LL res = 0;
    for (LL i = x; i; i -= lowbit(i))
        res += t[i];
    return res;
}

inline LL psum(LL x)
{
    return sum(t1, x) * (x + 1) - sum(t2, x);
}

int main()
{
    scanf("%lld%lld", &n, &m);
    for (LL i = 1; i <= n; i ++ ) scanf("%lld", &a[i]);
    for (LL i = 1; i <= n; i ++ )
    {
        LL b = a[i] - a[i - 1];
        add(t1, i, b);
        add(t2, i, b * i);
    }

    while (m -- )
    {
        char op[2];
        LL l, r, d;
        scanf("%s%lld%lld", op, &l, &r);
        if (op[0] == '2')
        {
            printf("%lld\n", psum(r) - psum(l - 1));
        }
        else
        {
            scanf("%lld", &d);
            add(t1, l, d), add(t2, l, l * d);
            add(t1, r + 1, -d), add(t2, r + 1, -d * (r + 1));
        }
    }

    return 0;
}

---

最后，如果觉得对您有帮助的话，点个赞再走吧！

（后附极限卡常代码，70ms，较优解）

#define qwq optimize
#pragma GCC qwq(1)
#pragma GCC qwq(2)
#pragma GCC qwq(3)
#pragma GCC qwq("Ofast")
#pragma GCC qwq("inline")
#pragma GCC qwq("-fgcse")
#pragma GCC qwq("-fgcse-lm")
#pragma GCC qwq("-fipa-sra")
#pragma GCC qwq("-ftree-pre")
#pragma GCC qwq("-ftree-vrp")
#pragma GCC qwq("-fpeephole2")
#pragma GCC qwq("-ffast-math")
#pragma GCC qwq("-fsched-spec")
#pragma GCC qwq("unroll-loops")
#pragma GCC qwq("-falign-jumps")
#pragma GCC qwq("-falign-loops")
#pragma GCC qwq("-falign-labels")
#pragma GCC qwq("-fdevirtualize")
#pragma GCC qwq("-fcaller-saves")
#pragma GCC qwq("-fcrossjumping")
#pragma GCC qwq("-fthread-jumps")
#pragma GCC qwq("-funroll-loops")
#pragma GCC qwq("-fwhole-program")
#pragma GCC qwq("-freorder-blocks")
#pragma GCC qwq("-fschedule-insns")
#pragma GCC qwq("inline-functions")
#pragma GCC qwq("-ftree-tail-merge")
#pragma GCC qwq("-fschedule-insns2")
#pragma GCC qwq("-fstrict-aliasing")
#pragma GCC qwq("-fstrict-overflow")
#pragma GCC qwq("-falign-functions")
#pragma GCC qwq("-fcse-skip-blocks")
#pragma GCC qwq("-fcse-follow-jumps")
#pragma GCC qwq("-fsched-interblock")
#pragma GCC qwq("-fpartial-inlining")
#pragma GCC qwq("no-stack-protector")
#pragma GCC qwq("-freorder-functions")
#pragma GCC qwq("-findirect-inlining")
#pragma GCC qwq("-fhoist-adjacent-loads")
#pragma GCC qwq("-frerun-cse-after-loop")
#pragma GCC qwq("inline-small-functions")
#pragma GCC qwq("-finline-small-functions")
#pragma GCC qwq("-ftree-switch-conversion")
#pragma GCC qwq("-fqwq-sibling-calls")
#pragma GCC qwq("-fexpensive-optimizations")
#pragma GCC qwq("-funsafe-loop-optimizations")
#pragma GCC qwq("inline-functions-called-once")
#pragma GCC qwq("-fdelete-null-pointer-checks")
#include <iostream>
#include <cstdio>

#define lb(x) (x & (-x))

using namespace std;

typedef long long LL;

const LL N = 100010;

LL n, m;
LL a[N];
LL t1[N], t2[N];

char *p1, *p2, buf[N];
#define nc() (p1 == p2 && (p2 = (p1 = buf) +\
fread(buf, 1, N, stdin), p1 == p2) ? EOF : *p1 ++ )
LL read()
{
    LL x = 0, f = 1;
    char ch = nc();
    while (ch < 48 || ch > 57)
    {
        if (ch == '-') f = -1;
        ch = nc();
    }
    while (ch >= 48 && ch <= 57)
        x = (x << 3) + (x << 1) + (ch ^ 48), ch = nc();
    return x * f;
}

char obuf[N], *p3 = obuf;
#define putchar(x) (p3 - obuf < N) ? (*p3 ++ = x) :\
(fwrite(obuf, p3 - obuf, 1, stdout), p3 = obuf, *p3 ++ = x)
inline void write(LL x)
{
    if (!x)
    {
        putchar('0');
        return;
    }
    LL len = 0, k1 = x, c[40];
    if (k1 < 0) k1 = -k1, putchar('-');
    while (k1) c[len ++ ] = k1 % 10 ^ 48, k1 /= 10;
    while (len -- ) putchar(c[len]);
}

inline void add(LL t[], LL x, LL c)
{
    for (LL i = x; i <= n; i += lb(i))
        t[i] += c;
}

inline LL sum(LL t[], LL x)
{
    LL res = 0;
    for (LL i = x; i; i -= lb(i))
        res += t[i];
    return res;
}

inline LL psum(LL x)
{
    return sum(t1, x) * (x + 1) - sum(t2, x);
}

int main()
{
    n = read(), m = read();
    for (LL i = 1; i <= n; i ++ ) a[i] = read();
    for (LL i = 1; i <= n; i ++ )
    {
        LL b = a[i] - a[i - 1];
        add(t1, i, b);
        add(t2, i, b * i);
    }

    LL op, l, r, d;
    while (m -- )
    {
        op = read(), l = read(), r = read();
        if (op == 2) write(psum(r) - psum(l - 1)), putchar(10);
        else
        {
            d = read();
            add(t1, l, d), add(t2, l, l * d);
            add(t1, r + 1, -d), add(t2, r + 1, -d * (r + 1));
        }
    }
	fwrite(obuf, p3 - obuf, 1, stdout);
    return 0;
}