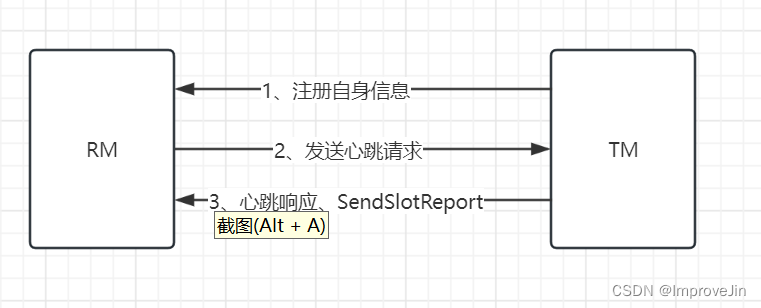
3.空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。
注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因
此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
实例1：

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

上面的冒泡排序我们在上篇文章说时间复杂度是O（N^2）,时间复杂度其实是O（1），这也和我们之前讲的大O渐进法差不多，我们看程序中创建变量都是常数项，所以就是O（1）.

空间复杂度一定要记住一个规则就是空间是不积累的，但是时间是累积的。

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
	if (n == 0)
		return NULL;
	long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n; ++i)
	{
		fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
	}
	return fibArray;
}

这是斐波那契的一个迭代，所以时间复杂度就是O（N），空间复杂度也是O（N），因为我们的malloc开辟了空间。

long long Fac(size_t N)
{
	if (N == 0)
		return 1;
	return Fac(N - 1) * N;
}

这个空间复杂度可能大家都会觉的是O（2^n）,但是其实是O（N），因为函数栈帧创建会销毁，有很多空间重复利用，这就是我们为什么说空间不是积累的，但是时间是积累的。
4. 常见复杂度对比
一般算法常见的复杂度如下：

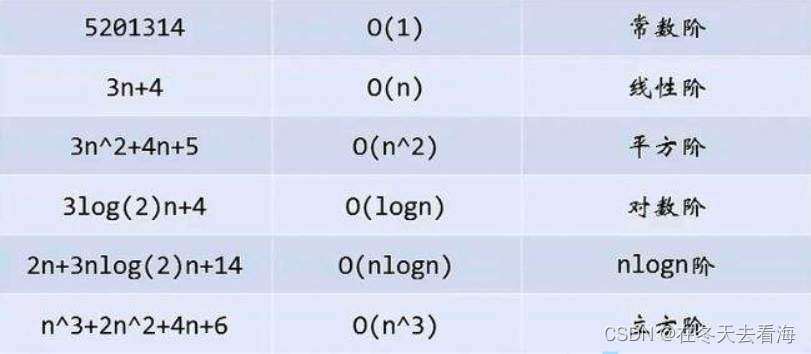
一般我们的算法后面几个不会用，太慢了。
下面给几个oj题，让大家做一做

题目一

思路1

我们可以用哈希的思想，就是先有一个数组，里面的内容都初始化-1，然后把数字是几就放到这个相应的数组当中，然后遍历一遍数组，如果是-1的话，那就是我们要找的值。

int missingNumber(int* nums, int numsSize){
        int*num=(int*)malloc(sizeof(int)*(numsSize+1));
        int i=0;
        for(i=0;i<=numsSize;i++)
        {
            num[i]=-1;
        }
        for(i=0;i<numsSize;i++)
        {
           num[nums[i]]=nums[i];
        }
        for(i=0;i<=numsSize;i++)
        {
            if(num[i]==-1)
            return i;
        }
        free(num);
        return NULL;
}

就是这样的一个思路

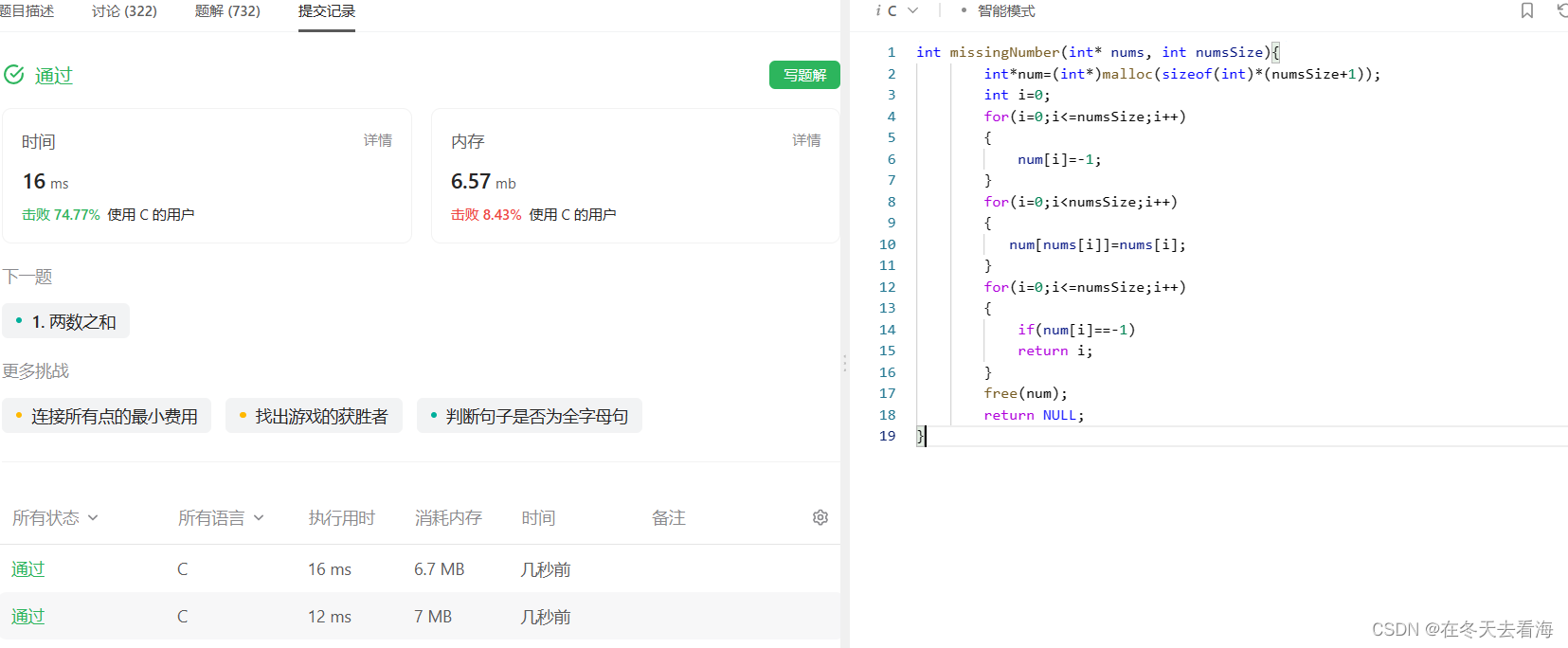
一开始写的时候一直在调那个编译错误，其实就是少了一个返回值，大家可以放到VS上调试，就像这样给一个主函数。

#include<stdio.h>
#include<stdlib.h>
int missingNumber(int* nums, int numsSize) {
    int* num = (int*)malloc(sizeof(int) * (numsSize + 1));
    int i = 0;
    for (i = 0; i <= numsSize; i++)
    {
        num[i] = -1;
    }
    for (i = 0; i < numsSize; i++)
    {
        num[nums[i]] = nums[i];
    }
    for (i = 0; i <= numsSize; i++)
    {
        if (num[i] == -1)
            return i;
    }
    free(num);
    return NULL;
}
int main()
{
	int arr[] = { 2,3,4,0 };
    int sz = sizeof(arr) / sizeof(arr[0]);
    int ret=missingNumber(arr, sz);
    printf("%d", ret);
	return 0;
}

思路2

按位异或，这是特别快的一个思路。因为我们0和任何数异或都是本身，然后我们只要给一个0就可以了，然后因为相同的数异或是0，接下来就看我们的代码。

int missingNumber(int* nums, int numsSize){
        int x=0;
        for(int i=0;i<numsSize;i++)
        {
            x^=nums[i];
        }
        for(int i=0;i<=numsSize;i++)
        {
            x^=i;
        }
        return x;
}

其实还有思路，但是我就不写了。给个思路吧
思路三，先排序，在找，按顺序一个一个遍历，但是空间复杂度肯定不是O（N），因为排序还要时间。
思路四，加0到N的数相加，然后减去这个数组，得到的就是消失的数。

旋转数

void revolve(int*left,int*right)
{
    while(left<right)
    {
        int tmp=*left;
        *left=*right;
        *right=tmp;
        left++;
        right--;
    }
}


void rotate(int* nums, int numsSize, int k){
        if(numsSize==1)
        return ;
        k=k%numsSize;
        revolve(nums,nums+numsSize-1);
        revolve(nums,nums+k-1);
        revolve(nums+k,nums+numsSize-1);
}

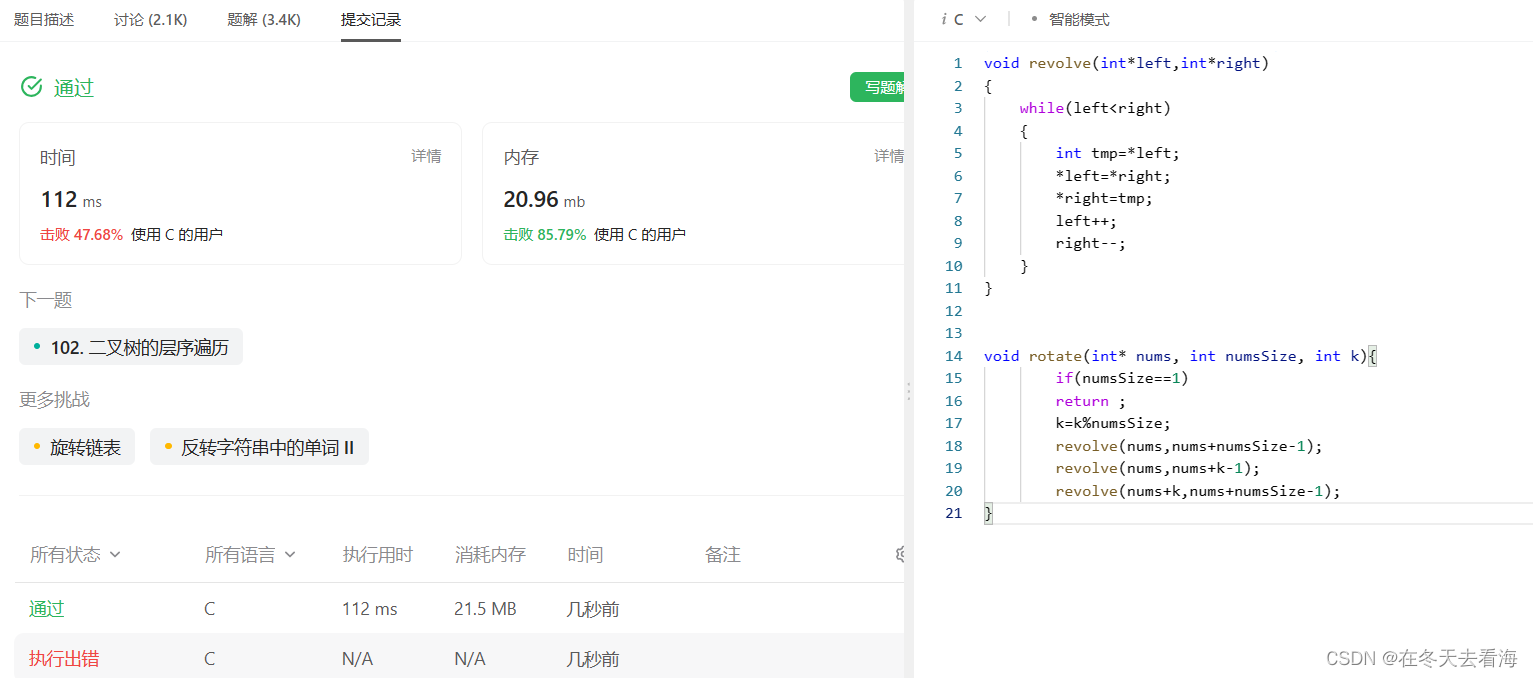
以上就是今天分享，我们下次再见