作者：Sachin Malhotra和Divya Godayal

        如果这些对你来说像希腊语，请阅读上一篇文章，复习马尔可夫链模型、隐马尔可夫模型和词性标记。

彼得的妈妈在离开前给你的状态图。

        在上一篇文章中，我们已经使用隐马尔可夫模型简要地模拟了词性标记的问题。

        彼得是否睡着的问题只是为了更好地理解这两篇文章中涉及的一些核心概念而提出的一个示例问题。这些文章的核心是使用隐马尔可夫模型解决词性标记问题。

        因此，在继续讨论维特比算法之前，让我们先看一下如何使用HMM对标记问题进行建模的更详细的解释。

三、生成模型和噪声通道模型

        自然语言处理中的许多问题都是使用监督学习方法解决的。

        机器学习中的监督问题定义如下。我们假设训练示例 ...，其中每个示例由一个与标签 y（i） 配对的输入 x（i） 组成。我们使用 X 来指代可能的输入集，使用 Y 来指代可能的标签集。我们的任务是学习一个函数 f ： X → Y，它将任何输入 x 映射到标签 f（x）。(x(1), y(1))(x(m) , y(m))

        在标记问题中，每个x（i）将是一个单词序列，每个y（i）将是一个标签序列（我们使用n（i）来指代第i个训练示例的长度）。X 将引用所有序列 x1 的集合。 . .xn，而 Y 将是所有标签序列 y1 的集合。 . .哎呀。我们的任务是学习一个函数f：X→Y，它将句子映射到标签序列。X1 X2 X3 …. Xn(i)Y1 Y2 Y3 … Yn(i)

        获得此问题估计值的直观方法是使用条件概率。 这是给定输入 x 的输出 y 的概率。将使用训练样本估计模型的参数。最后，给定一个未知的输入，我们希望找到p(y | x)x

f(x) = arg max(p(y | x)) ∀y ∊ Y

        这是在给定训练数据的情况下解决此通用问题的条件模型。机器学习和自然语言处理中主要采用的另一种方法是使用生成模型。

        在生成模型中，我们不是直接估计条件分布，而是模拟所有（x，y）对的联合概率。p(y|x)p(x, y)

我们可以使用贝叶斯规则将联合概率进一步分解为更简单的值：

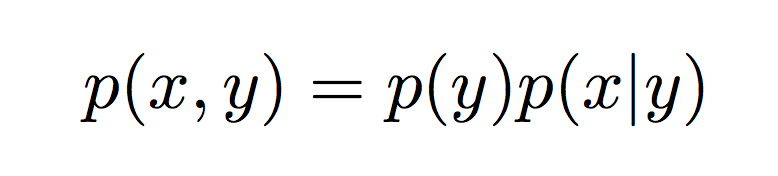
• p(y)是属于标签 y 的任何输入的先验概率。
• p(x | y)是给定标签 y 的输入 x 的条件概率。

我们可以使用此分解和贝叶斯规则来确定条件概率。

请记住，我们想要估计函数

f(x) = arg max( p(y|x) ) ∀y ∊ Y
f(x) = arg max( p(y) * p(x | y) )

        我们在这里跳过分母的原因是，无论考虑什么输出标签，概率都保持不变。因此，从计算的角度来看，它被视为规范化常数，通常被忽略。p(x)

        将联合概率分解为项的模型，通常称为噪声通道模型。直观地，当我们看到一个测试示例 x 时，我们假设它是分两步生成的：p(y)p(x|y)

1. 首先，选择了一个概率为 p（y） 的标签 y
2. 其次，示例 X 是从分布 p（x|y） 生成的。模型 p（x|y） 可以解释为一个“通道”，它将标签 y 作为其输入，并破坏它以产生 x 作为其输出。

四、词性标记模型的生成部分

        让我们假设一组有限的词 V 和一个有限的标签序列 K。然后集合 S 将是所有序列的集合，标记对使得 n > 0 和 。<x1, x2, x3 ... xn, y1, y2, y3, ..., yn>∀x ∊ V∀y ∊ K

        然后，生成标记模型是其中

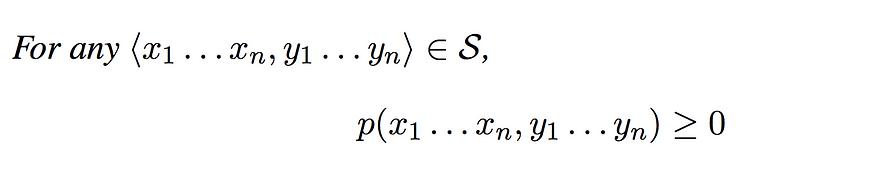
2.

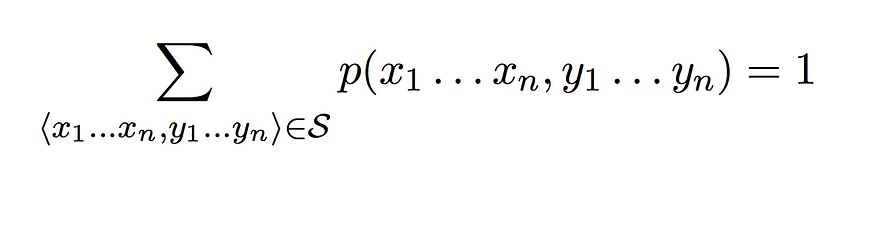
        给定一个生成标记模型，我们之前讨论的从输入到输出的函数变为

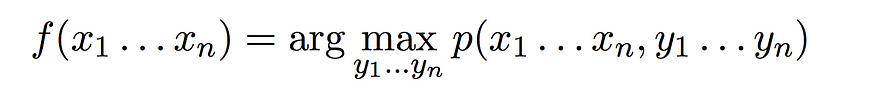
        因此，对于任何给定的单词输入序列，输出是模型中最高概率的标记序列。定义生成模型后，我们需要弄清楚三件不同的事情：

1. 我们如何准确定义生成模型概率p(<x1, x2, x3 ... xn, y1, y2, y3, ..., yn>)
2. 我们如何估计模型的参数，以及
3. 我们如何有效地计算

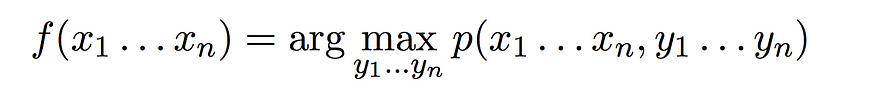
        让我们看看如何并排回答这三个问题，一次是针对我们的示例问题，然后是手头的实际问题：词性标记。

五、定义生成模型

        让我们首先看看如何使用HMM估计概率。p(x1 .. xn, y1 .. yn)

       我们可以拥有任何 N 元语法 HMM，它考虑大小为 N 的上一个窗口中的事件。

       下面提供的公式对应于三元组隐马尔可夫模型。

5.1 三元隐马尔可夫模型

        三元组隐马尔可夫模型可以使用

• 一组有限的状态。
• 一系列观测值。
• q（s|u， v）
  转移概率定义为在观测序列中观察“u”和“v”后立即出现状态“s”的概率。
• e（x|s）
  发射概率定义为在状态为 s 的情况下进行观测 x 的概率。

然后，生成模型概率估计为

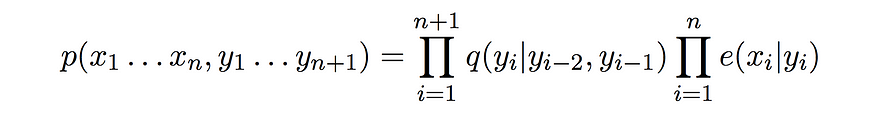
        至于我们正在考虑的婴儿睡眠问题，我们只有两种可能的状态：婴儿要么醒着，要么睡着了。随着时间的推移，看守人只能进行两次观察。房间要么有噪音进来，要么房间绝对安静。观测值和状态的顺序可以表示如下：

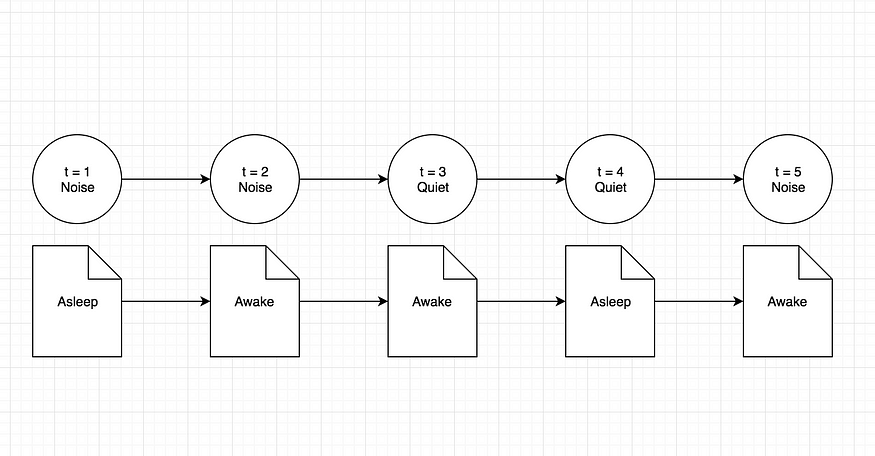
        随时间推移对婴儿睡眠问题的观察和状态

        进入词性标记问题，状态将由分配给单词的实际标签表示。这些话将是我们的观察。我们之所以说标签是我们的状态，是因为在隐马尔可夫模型中，状态总是隐藏的，我们所拥有的只是我们可见的一组观察。按照类似的思路，词性标记问题的状态和观察顺序将是

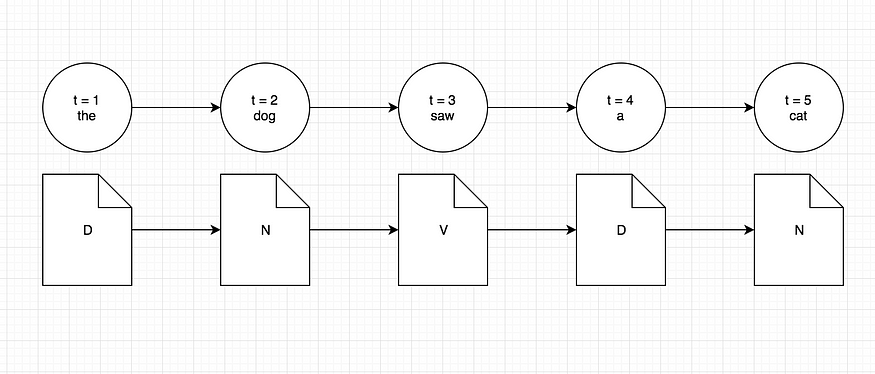
        POS 标记问题的观察结果和状态随时间推移

六、估计模型的参数

        我们假设我们可以访问一些训练数据。训练数据由一组示例组成，其中每个示例都是由观测值组成的序列，每个观测值都与状态相关联。鉴于这些数据，我们如何估计模型的参数？

        估计模型的参数是通过从我们拥有的训练语料库中读取各种计数来完成的，然后计算最大似然估计：

        三元组HMM的跃迁概率和发射概率

        我们已经知道，第一项表示转移概率，第二项表示排放概率。让我们看看上述术语中的四个不同计数的含义。

1. c（u， v， s） 表示状态 u、v 和 s 的三元组计数。这意味着它表示三种状态u，v和s在训练语料库中按该顺序一起出现的次数。
2. C（u， v） 遵循与三元组计数类似的思路，这是给定训练语料库的 U 和 V 状态的双元语法计数。
3. c（s → x） 是训练集中状态 s 和观测值 x 相互配对的次数。最后，
4. c（s） 是观测值被标记为状态 s 的先验概率。

        让我们先看一下玩具问题的样本训练集，看看使用它的跃迁和发射概率的计算。

        蓝色标记表示跃迁概率，红色表示发射概率计算。

        请注意，由于示例问题只有两个不同的状态和两个不同的观察值，并且给定训练集非常小，因此下面针对示例问题的计算使用的是双元 HMM 而不是三元组 HMM。

        彼得的母亲保留着观察和状态的记录。因此，她甚至为您提供了一个训练语料库，以帮助您获得过渡和发射概率。

6.1 转移概率示例：

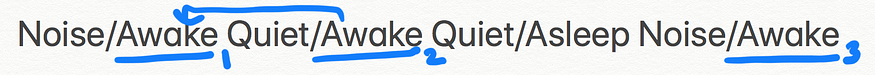
        训练语料库

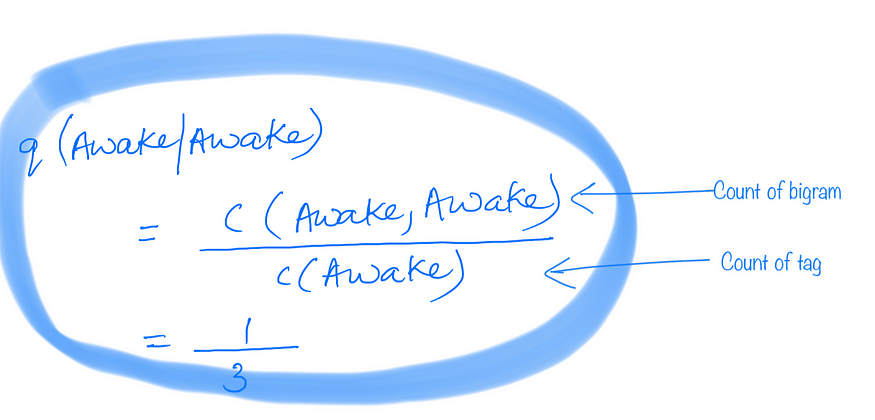
        清醒后出现的清醒计算

6.2 发射概率示例：

训练语料库

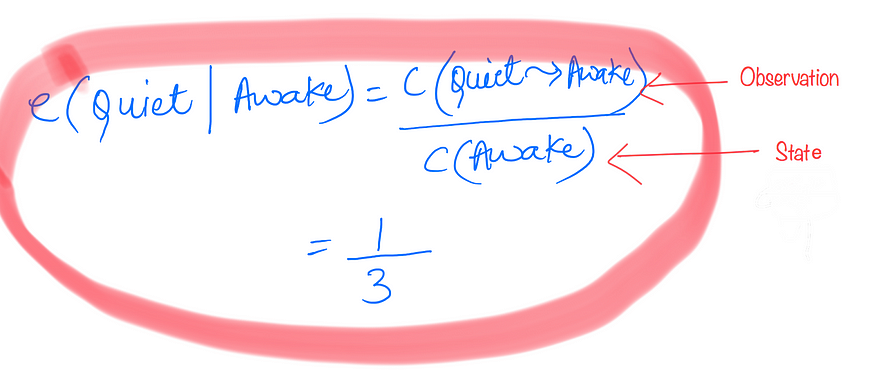
当状态为“清醒”时观察“安静”的计算

        这很简单，因为训练集非常小。让我们看一个示例训练集，用于解决词性标记的实际问题。在这里，我们可以考虑一个三元组 HMM，我们将相应地显示计算结果。

        我们将使用以下句子作为训练数据的语料库（符号单词/TAG 表示用特定词性标签标记的单词）。

        我们拥有的训练集是一个标记的句子语料库。每个句子都由标有相应词性标签的单词组成。例如：- eat/VB表示单词是“eat”，并且在此上下文中该句子中的词性标签是“ VB”，即动词短语。让我们看一个过渡概率和发射概率的示例计算，就像我们看到婴儿睡眠问题一样。

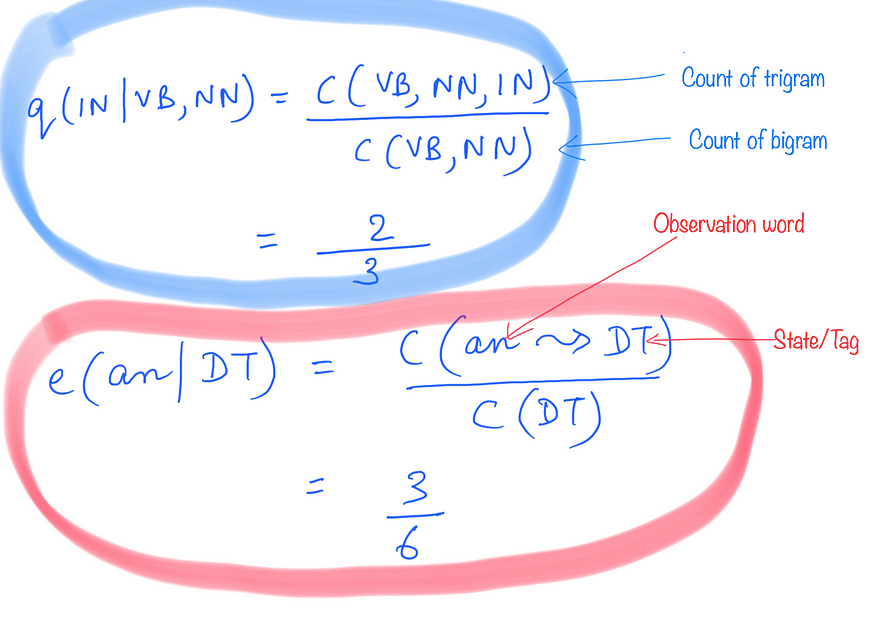
6.3 转移概率

        假设我们要计算转移概率 q（IN |VB，NN）。为此，我们可以看到我们以该特定顺序在训练语料库中看到三元组（VB，NN，IN）的次数。然后，我们将它除以我们在语料库中看到双字母（VB，NN）的总次数。

6.4 发射概率

        假设我们想找出发射概率e（an |DT）。为此，我们看到单词“an”在语料库中被标记为“DT”的次数，并将其除以我们在语料库中看到标签“DT”的总次数。

        因此，如果您查看这些计算，它表明计算模型的参数在计算上并不昂贵。也就是说，我们不必对训练数据进行多次传递来计算这些参数。我们所需要的只是一堆不同的计数，而单次遍历训练语料库应该为我们提供这一点。

        让我们继续看一下我们需要查看给定生成模型的最后一步。这一步是有效的计算

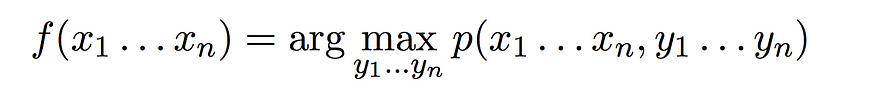
        我们将研究著名的维特比算法进行此计算。

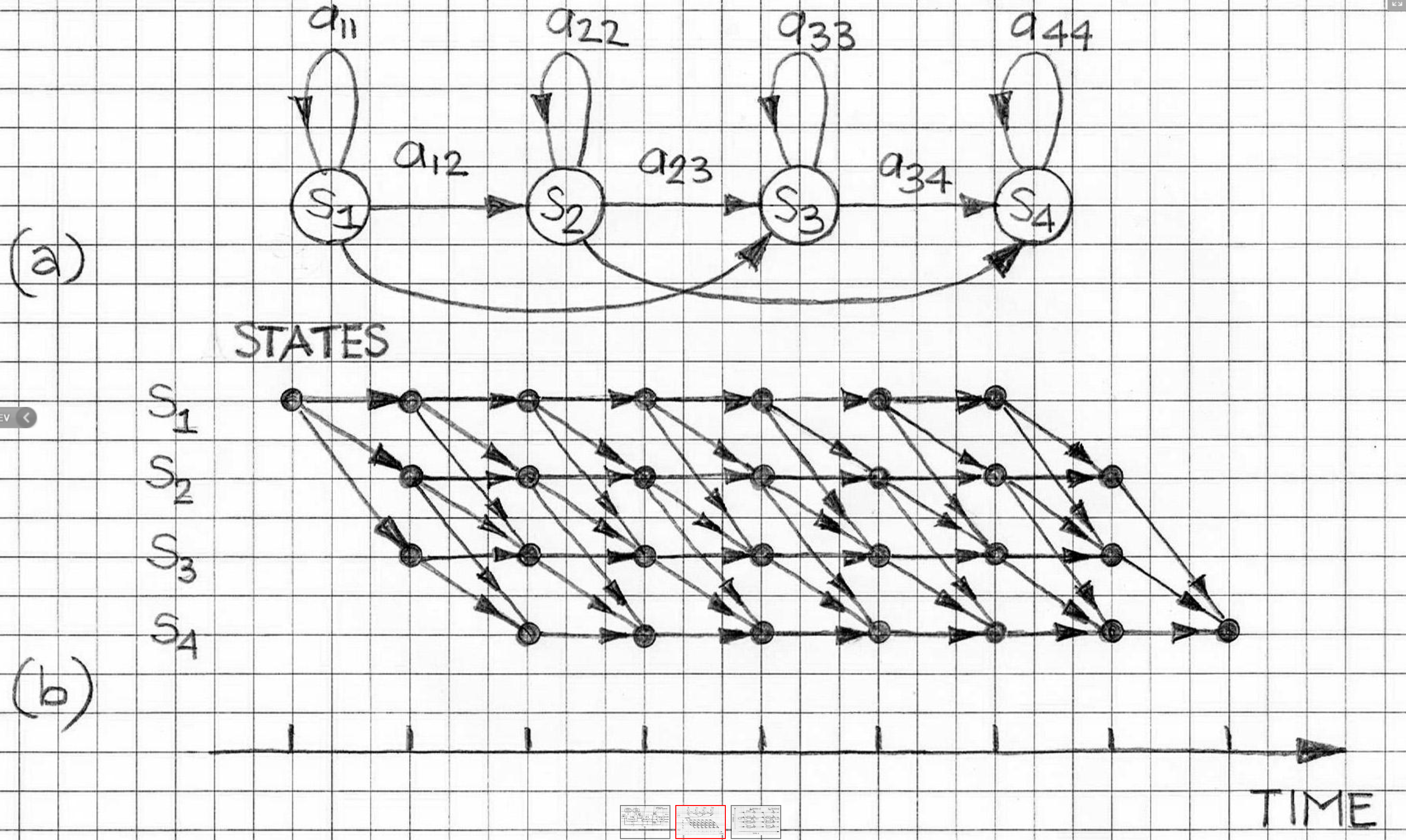
七、寻找最可能的序列 — 维特比算法

        最后，我们将解决在给定一组观察值 x1 的情况下找到最可能的标签序列的问题......xn.也就是说，我们要找出答案

        这里的概率用我们在本文上一节中学习如何计算的跃迁和发射概率来表示。只是为了提醒您，给定“n”个时间步长的观察序列的标签序列的概率公式为

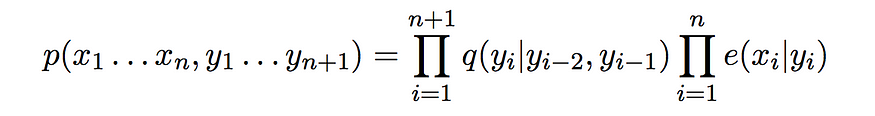
        在研究解决此问题的优化算法之前，让我们先看一下解决此问题的简单蛮力方法。基本上，我们需要从一组有限的可能标签序列中找出给定一组观察值的最可能的标签序列。让我们看一下示例问题和词性标记问题的一个小示例的可能序列总数。

        假设我们有以下一组针对示例问题的观察结果。

Noise     Quiet     Noise

我们有两个可能的标签{睡着和醒着}。上述观察结果的一些可能的标签序列是：

Awake      Awake     Awake
Awake      Awake     Asleep
Awake      Asleep    Awake
Awake      Asleep    Asleep

        总的来说，我们可以有 2³ = 8 个可能的序列。这可能看起来不是很多，但如果我们随着时间的推移增加观察的数量，序列的数量将呈指数级增长。当我们只有两个可能的标签时，就是这种情况。如果我们有更多呢？与词性标记的情况一样。

例如，考虑句子

the dog barks

        假设可能的标签集是{D，N，V}，让我们看看一些可能的标签序列：

D     D     D
D     D     N
D     D     V
D     N     D
D     N     N
D     N     V ... etc

        在这里，我们将有 3³ = 27 个可能的标签序列。正如你所看到的，这句话非常短，标签的数量也不是很多。在实践中，我们可以有比三个单词大得多的句子。然后，我们可以使用的唯一标签的数量也太高，无法遵循此枚举方法并以这种方式找到最佳标记序列。

        因此，序列数量的指数增长意味着对于任何合理长度的句子，蛮力方法都不会奏效，因为它需要太多时间来执行。

        我们将看到，我们可以使用称为维特比算法的动态规划算法有效地找到最高可能的标签序列，而不是这种蛮力方法。

        让我们首先定义一些对定义算法本身有用的术语。我们已经知道，给定一组观测值的标签序列的概率可以用转移概率和发射概率来定义。从数学上讲，它是

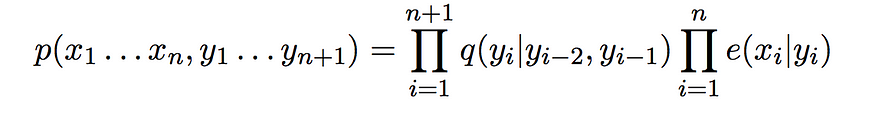
        让我们看一下这个的截断版本，它是

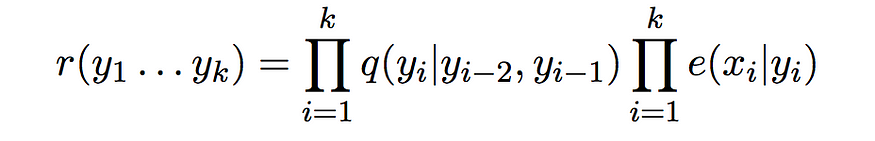
        让我们称之为长度为 k 的序列的成本。

        所以“r”的定义只是考虑概率定义的前k项，其中k ∊ {1..n}和任何标签序列y1...是的。

        接下来我们有集合 S（k， u， v），它基本上是长度为 k 的所有标签序列的集合，以双字母 （u， v） 结尾，即

        最后，我们定义术语 π（k， u， v），它基本上是具有最大成本的序列。

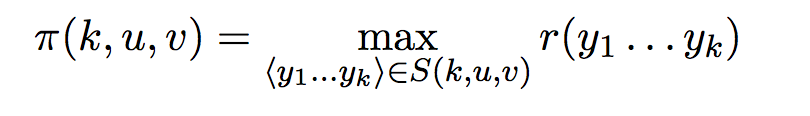
        维特比算法背后的主要思想是，我们可以以递归、记忆的方式有效地计算术语 π（k， u， v） 的值。为了递归定义算法，让我们看一下递归的基本情况。

π(0, *, *) = 1
π(0, u, v) = 0

        由于我们正在考虑一个三元组HMM，我们将考虑将所有三元组作为维特比算法执行的一部分。

        现在，我们可以从句子的前三个单词开始第一个三元组窗口，但随后模型将错过第一个单词或前两个单词独立出现的三元组。出于这个原因，我们认为两个特殊的开始符号是这样，所以我们的句子变成了*

*    *    x1   x2   x3   ......         xn

我们考虑的第一个三元组是（*，*，x1），第二个是（*，x1，x2）。

现在我们已经有了所有的术语，我们终于可以看看算法的递归定义，它基本上是算法的核心。

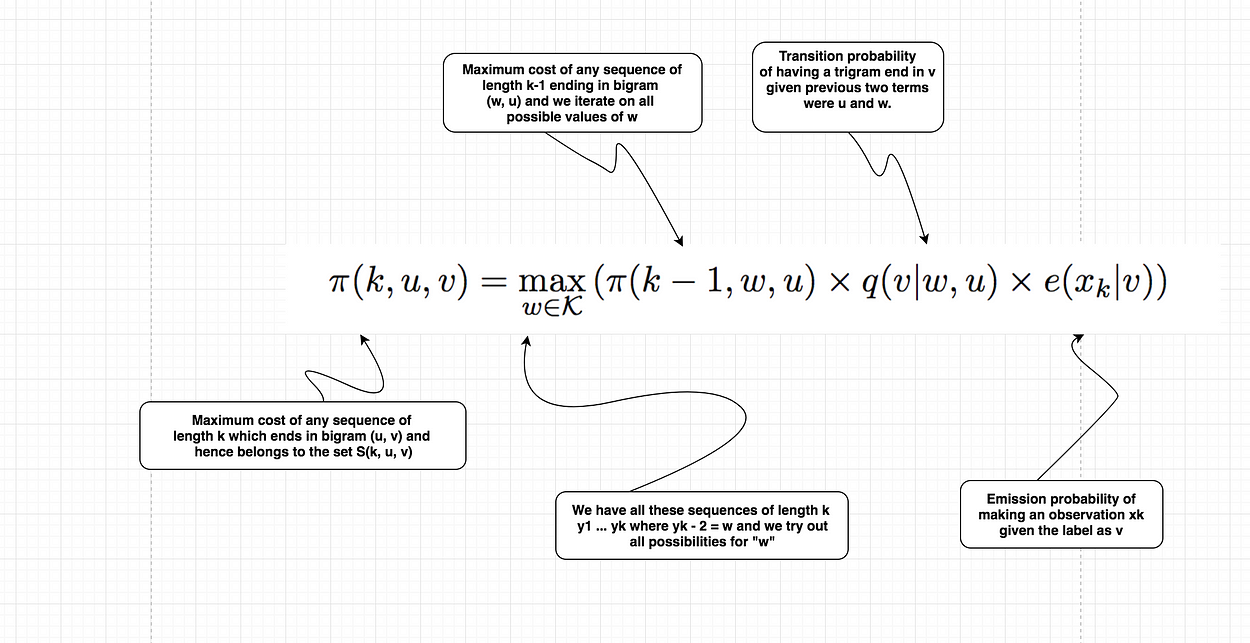
        这个定义显然是递归的，因为我们试图计算一个π项，而我们正在使用它的递归关系中使用另一个值较低的 k 项。

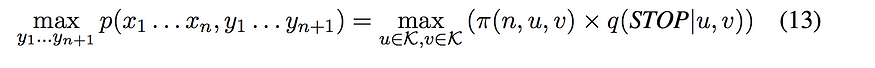
        每个序列都将以一个特殊的 STOP 符号结尾。对于三元组模型，我们还会在开头有两个特殊的开始符号“*”。

        看看整个算法的伪代码。

        该算法首先使用递归
        定义填充 π（k， u， v） 值。然后，它使用前面描述的恒等式来计算任何序列的最高概率。

        算法的运行时间为 O（n|K|³），因此它在序列的长度上是线性的，在标签的数量上是立方的。

        注意：我们将仅显示基于双字母HMM的婴儿睡眠问题和词性标记问题的计算。三元组的计算留给读者自己做。但是本文末尾附加的代码基于三元组 HMM。只是在考虑双元 HMM 而不是三元组 HMM 时，维特比算法的计算更容易解释和描绘。

        因此，在展示维特比算法的计算之前，让我们看一下基于双元词 HMM 的递归公式。

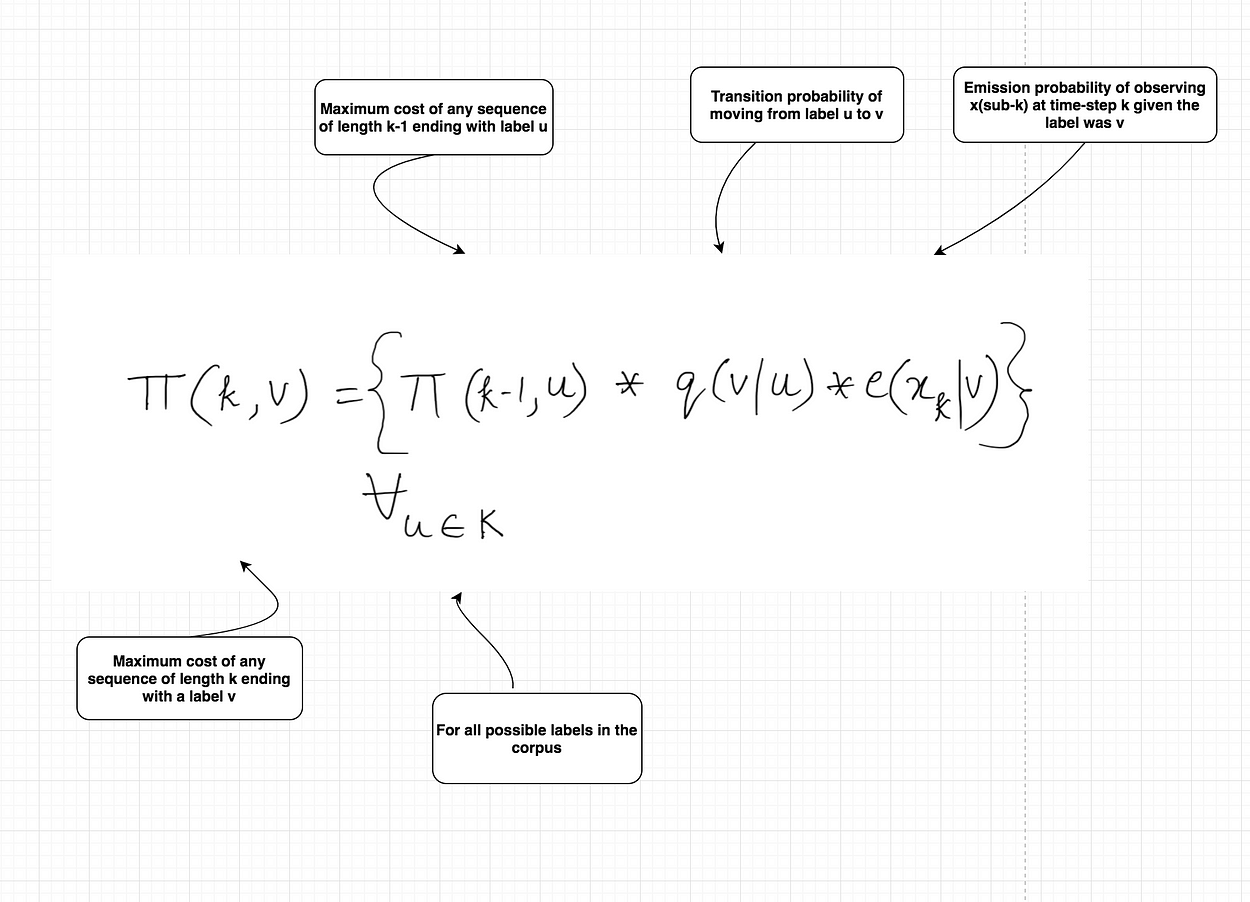
        这个与我们之前看到的三元组模型非常相似，只是现在我们只关注当前标签和之前的标签，而不是之前的两个标签。算法的复杂性现在变为 O（n|K|²）。

7.1 婴儿睡眠问题的计算

        现在我们已经为 Viterbi 算法准备好了递归公式，让我们先看看我们遇到的示例问题（即婴儿睡眠问题）的相同计算示例，然后是词性标记版本。

        请注意，当我们处于这一步时，即维特比算法的计算，以在一系列时间步长内给定一组观测值的情况下找到最可能的标签序列，我们假设已经从给定的语料库中计算了过渡和发射概率。让我们看一下婴儿睡眠问题的跃迁和发射概率样本，我们将用于计算算法。

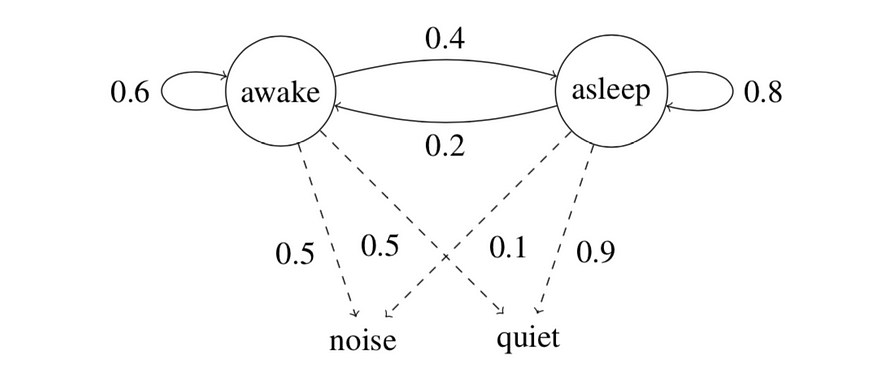
        婴儿从清醒开始，并在房间里停留三个时间点，t1 。t3（马尔可夫链的三次迭代）。观察结果是：安静，安静，噪音。请看下图，其中显示了最多两个时间步长的计算。之后将显示包含所有最终值集的完整图表。

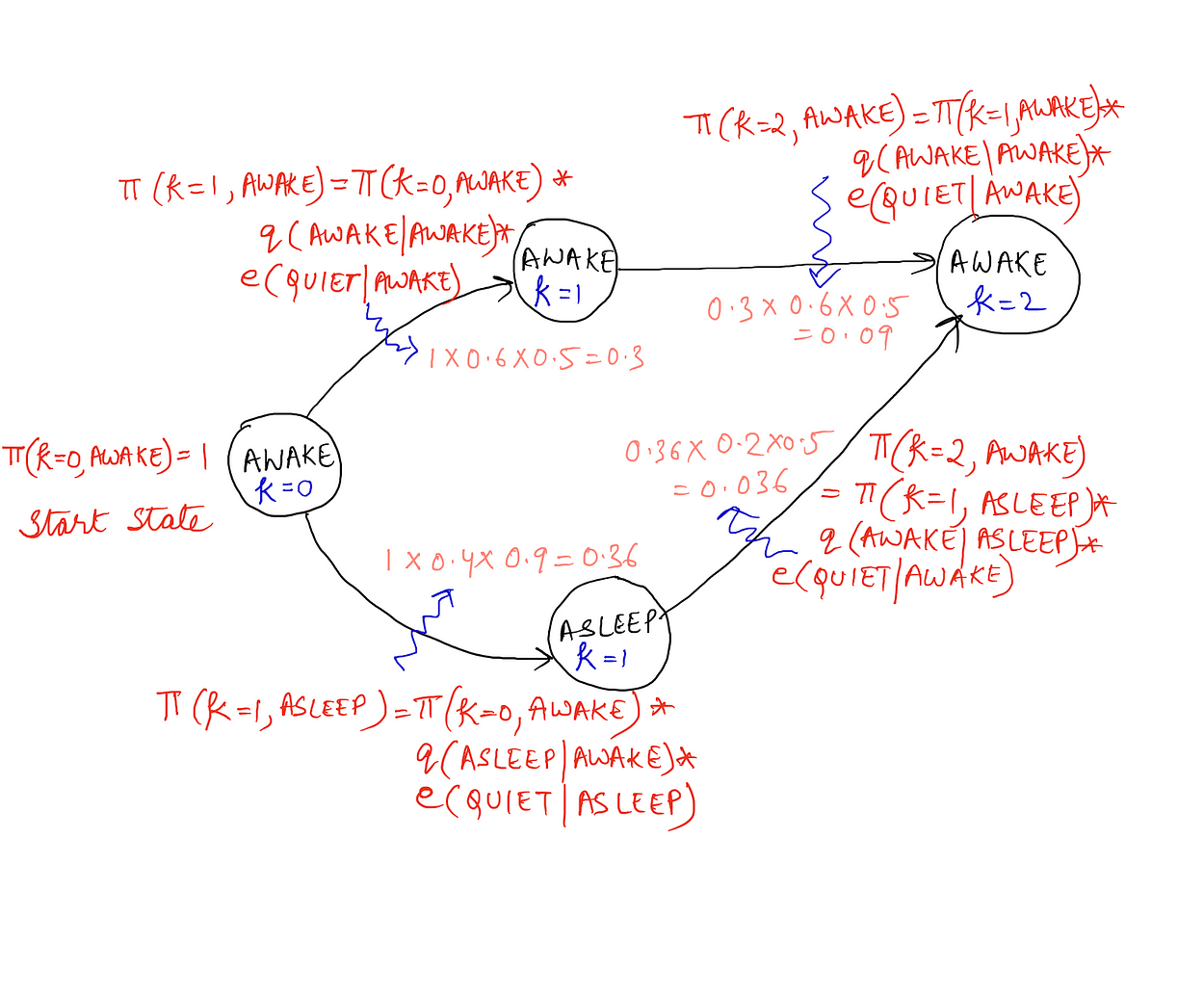
        为了简单起见，我们没有在上图中显示 k = 2 时“睡眠”状态的计算和 k = 3 的计算。

        现在我们已经完成了所有这些计算，我们想要计算婴儿在不同给定时间步长中可能处于的最可能的状态序列。因此，对于 k = 2 和唤醒状态，我们想知道在 k = 1 处转换到唤醒时最可能的状态 k = 2。（k = 2 表示从 3 开始的长度为 0 的状态序列，t = 2 表示时间步长 2 的状态。我们得到的状态是 t = 0，即唤醒）。

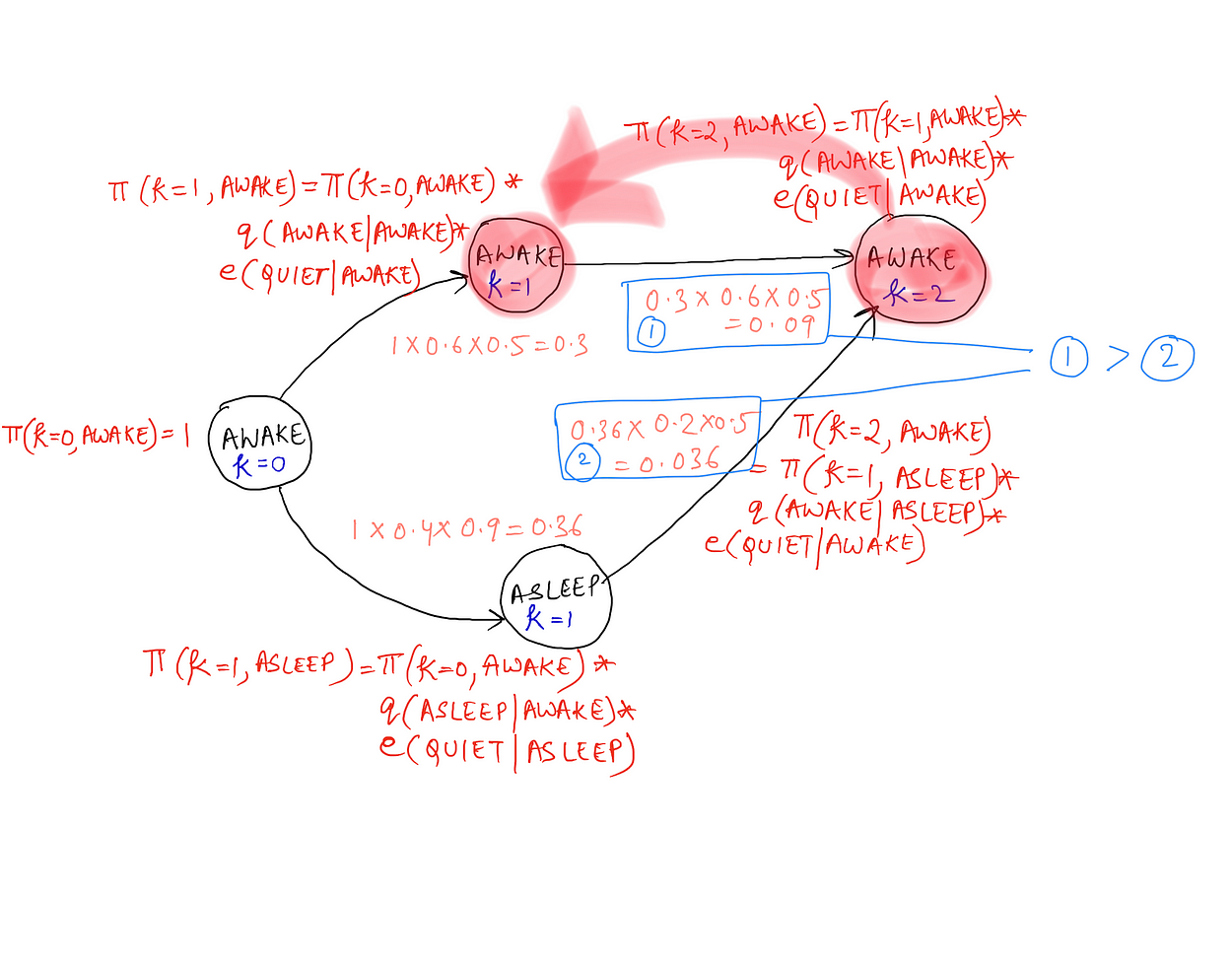
        显然，如果时间步长 2 的状态是 AWAKE，那么时间步长 1 的状态也会是 AWAKE，正如计算所指出的那样。因此，维特比算法不仅帮助我们找到π（k）值，即使用动态规划概念的所有序列的成本值，而且还帮助我们找到给定开始状态和观察序列的最可能的标签序列。下面给出了算法以及用于存储反向指针的伪代码。

7.2 词性标记问题的计算

        让我们看一下词性标记的稍大语料库和相应的维特比图，显示了维特比算法的计算和反向指针。

        以下是我们将考虑的语料库：

        现在看一下从这个语料库计算的转移概率。

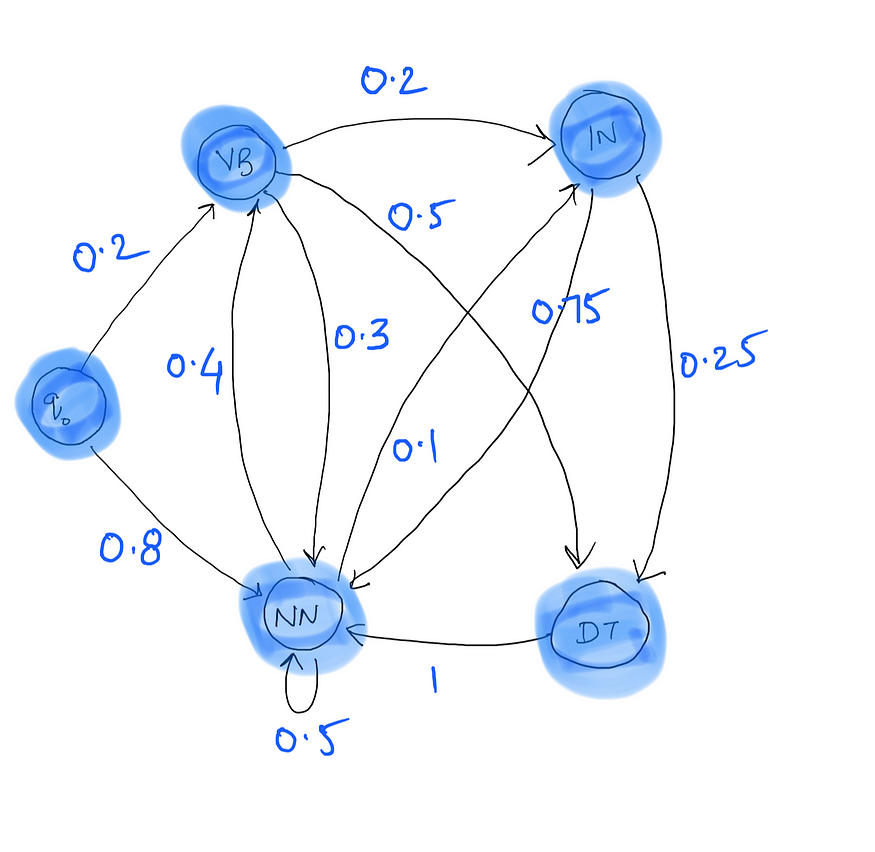
        在这里，q0 → VB 表示以标签 VB 开头的句子的概率，即句子的第一个单词被标记为 VB。同样，q0 → NN 表示以标签 NN 开头的句子的概率。 请注意，在语料库中的 10 个句子中，8 个以 NN 开头，2 个以 VB 开头，因此是相应的转换概率。

        至于发射概率，理想情况下，我们应该查看语料库中标签和单词的所有组合。由于这太多了，我们将只考虑维特比算法计算中使用的句子的发射概率。

Time flies like an arrow 

上述句子的发射概率为：

最后，我们准备好查看给定句子、转移概率、发射概率和给定语料库的计算。

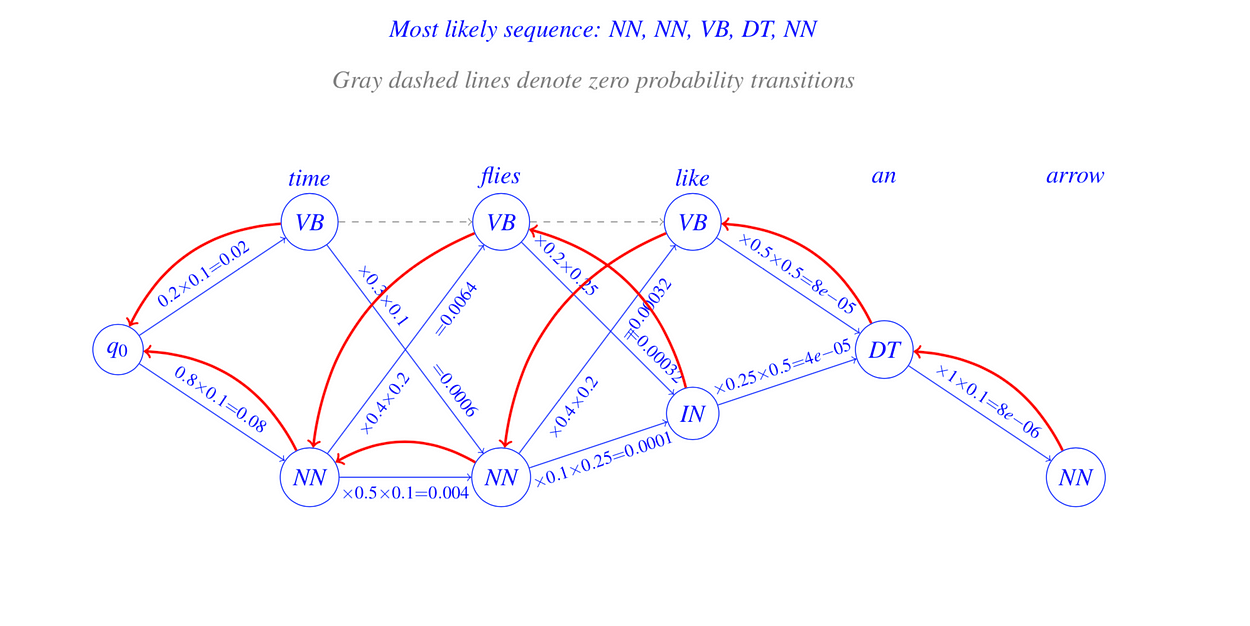
        那么，这就是维特比算法的全部内容吗？看看下面的例子。

        每个单词下面的存储桶填充了训练语料库中该单词旁边可能看到的标签。给定的句子可以具有标签组合，具体取决于我们采取的路径。但是有一个问题！你能猜出那是什么吗？

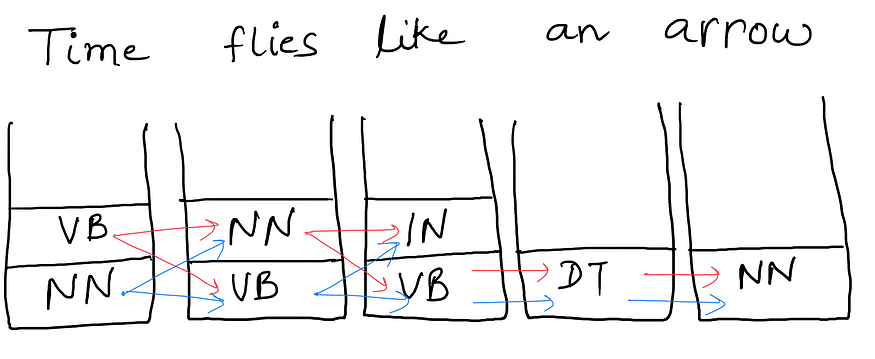
序列路径的所有组合

你能弄清楚吗？

不？？

让我告诉你它是什么。

计算图中可能存在一些我们没有转移概率的路径。因此，我们的算法可以丢弃该路径并采用另一条路径。

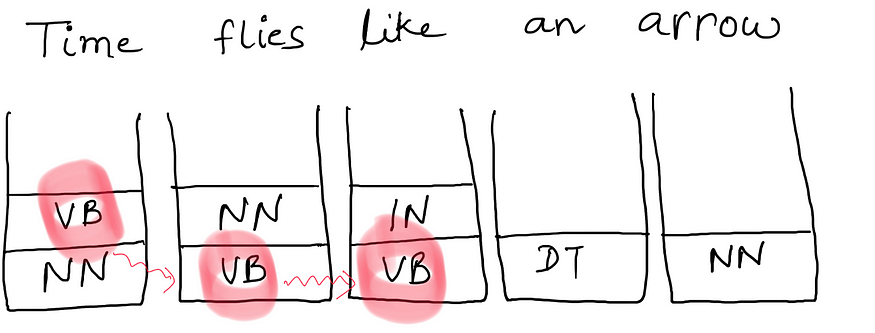
        在上图中，我们丢弃标记为红色的路径，因为我们没有 q（VB|VB）。训练语料库从来没有 VB 后跟 VB。因此，在维特比计算中，我们最终采用 q（VB|VB） = 0。如果你一直密切关注算法，你会发现计算中的单个0将使标签/标签序列的整个概率或最大成本为0。

        然而，这意味着我们忽略了训练语料库中没有看到的组合。

        这是处理现实世界示例的正确方法吗？

        考虑上面句子中的一个小调整。

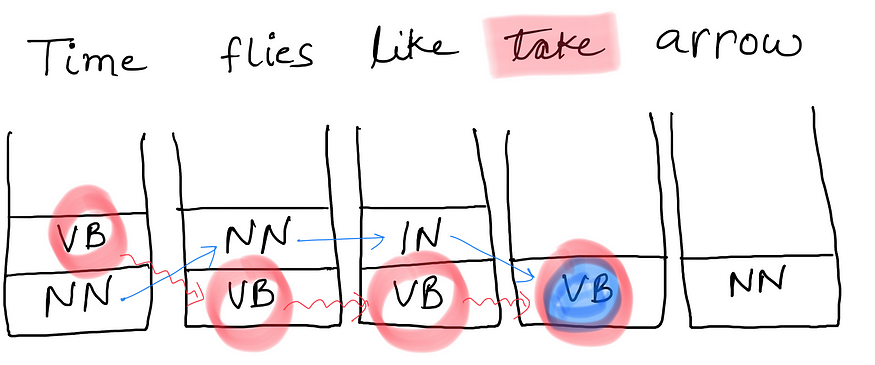
时间过得飞快，就像拿箭一样

        在这句话中，我们没有任何替代路径。即使我们有维特比概率，直到我们到达“喜欢”这个词，我们也无法继续前进。由于两个 q（VB|VB） = 0 和 q（VB|IN） = 0。我们现在该怎么办？

        我们在这里考虑的语料库非常小。考虑任何具有大量单词的合理大小的语料库，我们有一个主要的数据稀疏性问题。看看下面。

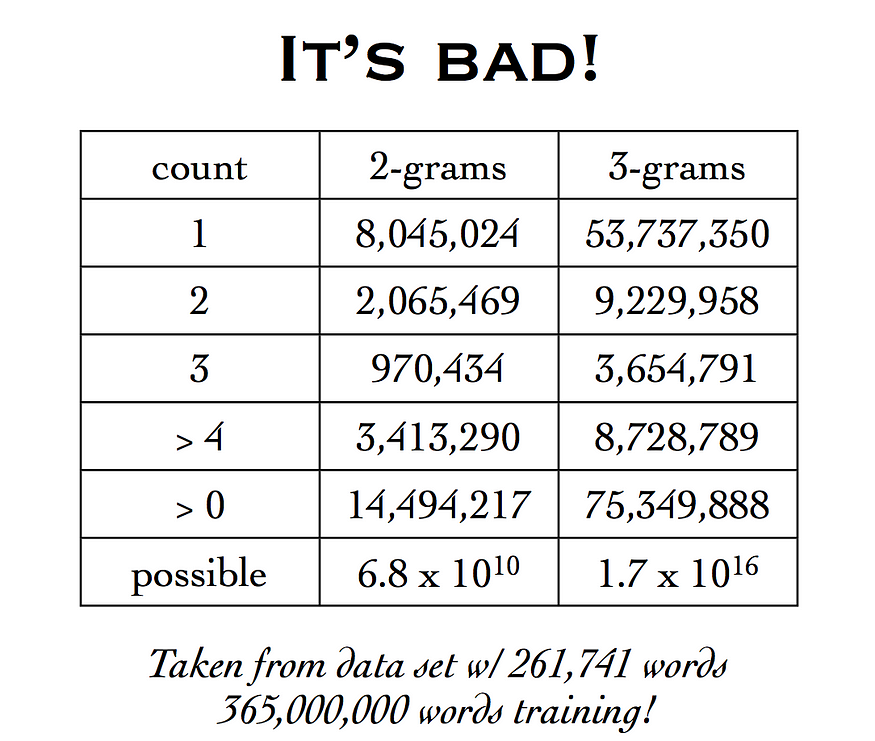
来源： http://www.cs.pomona.edu/~kim/CSC181S08/lectures/Lec6/Lec6.pdf

        这意味着我们可以有潜在的68亿双字母，但语料库中的单词数量不到十亿。这是大量的零转换概率需要填补。如果我们考虑三元组，数据的稀疏性问题甚至更加复杂。

        为了解决这个数据稀疏性问题，我们采用了一种称为平滑的解决方案。

八、平滑

        平滑背后的想法就是这样：

1. 折扣 ― 现有概率值有点和
2. 重新分配 — 此概率为零

        通过这种方式，我们重新分配非零概率值以补偿看不见的过渡组合。让我们考虑一种非常简单的平滑技术，称为拉普拉斯平滑。

        拉普拉斯平滑也称为单计数平滑。稍后您将确切地理解为什么它以这个名称命名。让我们修改一下如何在给定训练语料库的情况下计算三元组 HMM 模型的参数。

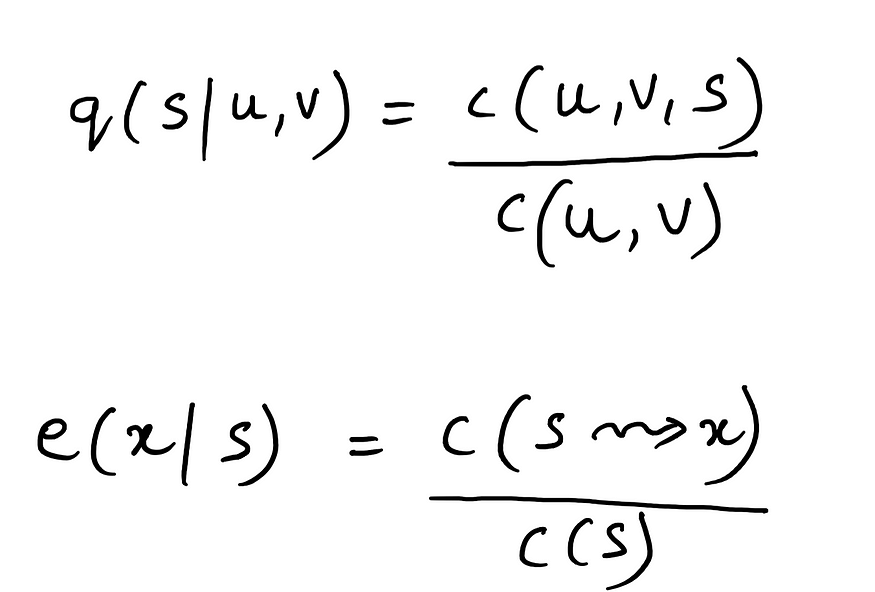
这里可能出错的值是

1. c(u, v, s)为 0
2. c(u, v)为 0
3. 我们在测试句中得到一个未知的单词，并且我们没有任何与之关联的训练标签。

所有这些都可以通过平滑来解决。因此，拉普拉斯平滑计数将变为

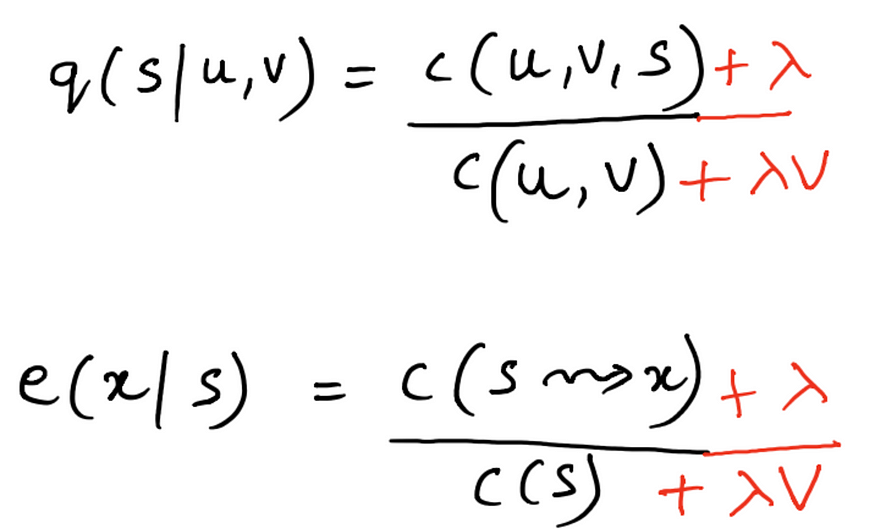
        这里 V 是我们语料库中标签的总数，λ 基本上是 0 到 1 之间的实际值。它就像一个折扣因素。λ = 1 值会给我们太多的概率值重新分布。 例如：

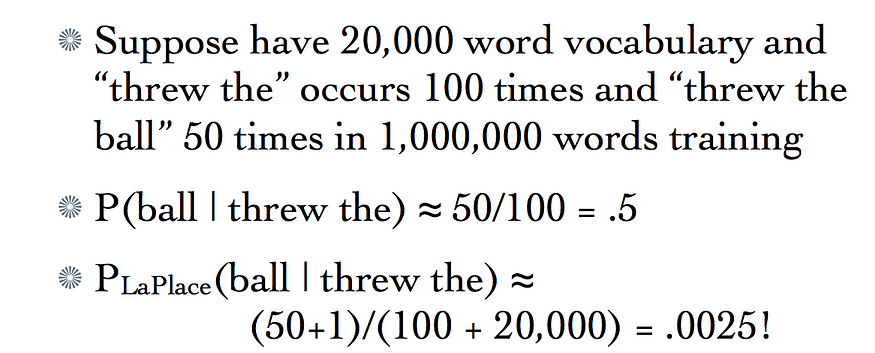
        对于 λ = 1，看不见的三元组被赋予了太多的权重，这就是为什么上述拉普拉斯平滑的修改版本被考虑用于所有实际应用的原因。贴现系数的值因应用而异。

        请注意，λ = 1 只有在词汇量太大时才会产生问题。对于较小的语料库，λ = 1 会给我们一个很好的开始性能。

        关于拉普拉斯平滑需要注意的一点是，它是一个均匀的再分布，也就是说，所有以前看不见的三元组都具有相等的概率。因此，假设我们得到一些数据，我们观察到

• 三元组的频率<给，那个，东西>为零
• 三元组的频率<给，认为>也是零
• 看不见的事件上的均匀分布意味着：
  P（thing|gve， the） = P（think|gve， the）

        这是否反映了我们对英语使用的了解？
        P（thing|gve， the） > P（think|gve， the） 理想情况下，但使用拉普拉斯平滑的均匀分布不会考虑这一点。

这意味着在我们的计算中考虑一个巨大的语料库中数百万个看不见的三元组时，它们的概率相等。这可能不是正确的做法。但是，最好考虑 0 概率，这会导致这些三元组并最终完全忽略维特比图中的某些路径。但这仍然需要努力和改进。

        然而，有许多不同类型的平滑技术可以改进基本的拉普拉斯平滑技术，并帮助克服概率均匀分布的问题。其中一些技术是：

• 好图灵估计
• 耶利内克-默瑟平滑（插值）
• 卡茨平滑（退避）
• 威滕-贝尔平滑
• 绝对折扣
• 克乃瑟-内伊平滑

        要更详细地阅读有关这些不同类型的平滑技术的更多信息，请参阅本教程。选择哪种平滑技术在很大程度上取决于手头的应用程序类型、正在考虑的数据类型以及数据集的大小。

        如果您一直在关注这篇冗长的文章，那么我必须说

来源： https://sebreg.deviantart.com/art/You-re-Kind-of-Awesome-289166787

        让我们继续看一下我们可以对 Viterbi 算法进行的轻微优化，它可以减少计算次数，并且对于那里的许多数据集也很有意义。

        但是，在此之前，请再次查看算法的伪代码。

如果我们仔细观察，我们可以看到，对于每个三元组单词，我们正在考虑所有可能的标签集。 也就是说，如果标签的数量是 V，那么我们正在考虑 |V|³ 测试句的每个三元组的组合数。

        暂时忽略三元组，只考虑一个单词。我们将考虑上述算法中给定单词的所有唯一标签。考虑一个语料库，其中我们有单词“kick”，它只与两个标签相关联，比如{NN，VB}，训练语料库中唯一标签的总数约为500（这是一个巨大的语料库）。

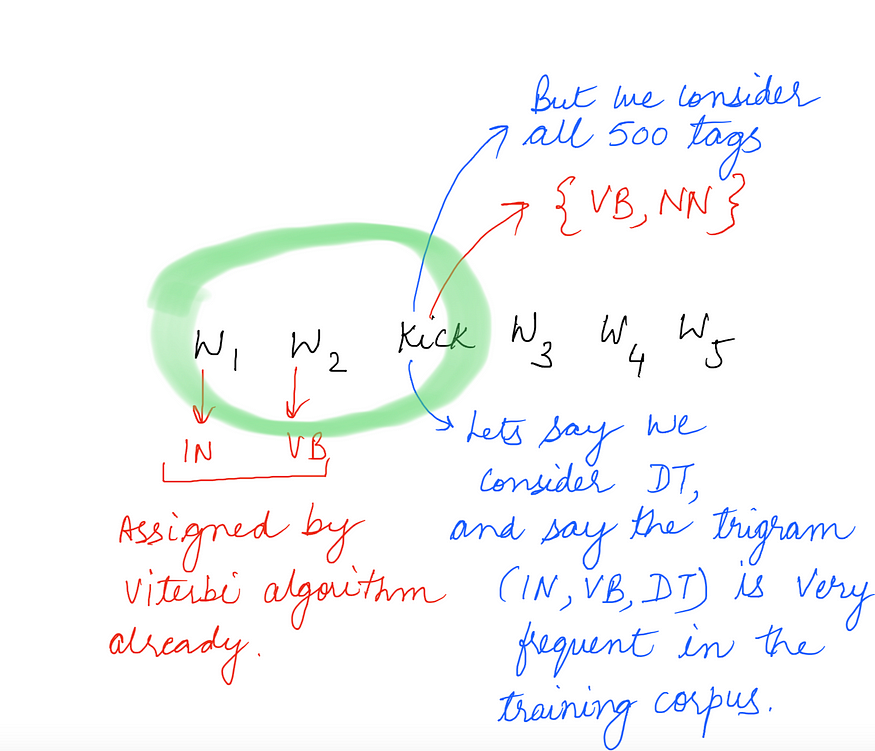
        现在这里的问题很明显了。我们最终可能会分配一个对所考虑的单词没有意义的标签，仅仅是因为以标签结尾的三元组的转换概率非常高，如上所示。此外，如果单词“kick”在整个语料库中仅出现两个唯一标签，那么考虑单词“kick”的所有 500 个标签在计算上效率低下。

        因此，我们所做的优化是，对于每个单词，我们只考虑语料库中出现的标签，而不是考虑语料库中的所有唯一标签。

        这将起作用，因为对于一个相当大的语料库，一个给定的单词理想情况下会出现在它可以出现的所有各种标签集（至少大多数）。那么简单地考虑维特比算法的那些标签是合理的。

        就维特比解码算法而言，复杂性仍然保持不变，因为我们总是关注最坏情况的复杂性。在最坏的情况下，每个单词都与语料库中的每个唯一标签一起出现，因此复杂性保持在 O（n|V|³） 表示三元组模型和 O（n|V|²） 表示双元模型。

        有关代码的递归实现，请参阅

        递归实现是与拉普拉斯平滑一起完成的。有关迭代实现，请参阅

        此实现是使用单计数平滑技术完成的，与拉普拉斯平滑相比，该技术具有更高的精度。

        两篇文章中公式和计算的很多快照都是从这里派生出来的。