leetCode刷题记录1

文章目录

- hot100题
- - 200. 岛屿数量
  - 206. 反转链表
  - 207. 课程表
  - 208. 实现 Trie (前缀树)
  - - ★ Student[] strArr= new Student[26];//真的只是创建了引用数组只是new了数组存放引用的内存并没有真的new对象内存
  - 215. 数组中的第K个最大元素
  - 221. 最大正方形
  - 226. 翻转二叉树
  - 234. 回文链表
  - 236. 二叉树的最近公共祖先
  - 238. 除自身以外数组的乘积
  - 240. 搜索二维矩阵 II
  - 279. 完全平方数
  - 283. 移动零
  - 287. 寻找重复数
  - 300. 最长递增子序列
  - 309. 最佳买卖股票时机含冷冻期
  - 322. 零钱兑换
  - 337. 打家劫舍 III
  - 338. 比特位计数
  - 347. 前 K 个高频元素
  - 394. 字符串解码
  - 406. 根据身高重建队列
  - 416. 分割等和子集
  - 437. 路径总和 III
  - 438. 找到字符串中所有字母异位词
  - 448. 找到所有数组中消失的数字
  - 461. 汉明距离
  - 494. 目标和
  - 538. 把二叉搜索树转换为累加树
  - 543. 二叉树的直径

hot100题

200. 岛屿数量

经典老题 D/BFS求连通分量个数
先用BFS写了一下，好多细节错误然后代码写得很糟糕

// 经典老题  D/BFS求连通分量个数
public int numIslands(char[][] grid) {
    N = grid.length;
    M = grid[0].length;
    this.grid = grid;
    visit = new boolean[N][M];
    int k = 0;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            if (!visit[i][j] && grid[i][j] == '1') {
                BFS(i, j);
                k++;
            }
        }
    }
    return k;
}

class Point {
    int x, y;
    Point() {}
    Point(int x, int y) {this.x = x;this.y = y;}
}

int M,N;
char[][] grid = null;
boolean[][] visit = null;

boolean judge(int x, int y) {
    if (x < 0 || y < 0 || x >= N || y >= M || visit[x][y] || grid[x][y] == '0') return false;//千万注意是字符'0'
    return true;
}

int[] dx = {1, -1, 0, 0};
int[] dy = {0, 0, 1, -1};

void BFS(int x, int y) {
    Queue<Point> q = new LinkedList<>();
    q.offer(new Point(x, y));
    visit[x][y] = true;

    while (!q.isEmpty()) {
        Point top = q.poll();
        //System.out.printf("(%d,%d) ",top.x+1,top.y+1);
        for (int i = 0; i < dx.length; i++) {
            int a = top.x + dx[i], b = top.y + dy[i];
            if (judge(a, b)) {
                q.offer(new Point(a, b));
                visit[a][b] = true;
            }
        }
    }
    //System.out.println();
}

看了题解，再去优化：
1、DFS代码要比BFS简单多了
2、遍历过的直接修改值为非1即可，不用专门准备visit数组了
3、DFS也不需要dx、dy数组，直接写四次dfs递归调用即可，看起来清爽多了

重写了一下，果然舒服多了，不要总想着c++那一套，太麻烦了：

// 经典老题  D/BFS求连通分量个数
public int numIslands(char[][] grid) {
    M = grid.length;
    N = grid[0].length;
    this.grid = grid;
    int res = 0;
    for (int i = 0; i < M; i++) {
        for (int j = 0; j < N; j++) {
            if (grid[i][j] == '1') {//千万注意是字符'1',不是数字1
                DFS(i, j);
                res++;
            }
        }
    }
    return res;
}

int M, N;
char[][] grid;

void DFS(int x, int y) {
    // 千万注意是字符'1',不是数字1
    if (x < 0 || x >= M || y < 0 || y >= N || grid[x][y] != '1') return;
    grid[x][y] = 2;//遍历过了 修改为2 (只要不是1就行了)
    //继续递归遍历连通的1
    DFS(x + 1, y);
    DFS(x - 1, y);
    DFS(x, y + 1);
    DFS(x, y - 1);
}

206. 反转链表

// 水题 拆下来 一个个头插 即可
public ListNode reverseList(ListNode head) {
    ListNode ans = new ListNode();//头结点
    while (head!=null){
        // 先摘下来
        ListNode t = head;
        head = head.next;
        // 再头插
        t.next = ans.next;
        ans.next = t;
    }
    return ans.next;
}

据说递归可以做这题

果然可以，类似后序遍历的写法，也很简单

ListNode ans = new ListNode();//头结点
ListNode pre = ans;
public ListNode reverseList(ListNode head) {
    if(head==null) return null;
    reverseList(head.next);
    pre.next = head;
    pre = head;
    pre.next = null;//防止最后一个没有尾巴
    return ans.next;
}

207. 课程表

// 经典拓扑排序
public boolean canFinish(int numCourses, int[][] prerequisites) {
    int[] indegree = new int[numCourses];
    int[][] matrix = new int[numCourses][numCourses];

    // 领接矩阵
    for (int i = 0; i < prerequisites.length; i++) {
        int a = prerequisites[i][0], b = prerequisites[i][1];
        matrix[b][a] = 1;//b->a   //邻接矩阵 同时也是hash表
        indegree[a]++; // 随便记录每个元素的入度
    }

    Stack<Integer> s = new Stack<>();
    for (int i = 0; i < numCourses; i++) {
        if (indegree[i] == 0) s.push(i);
    }

    int count = 0;
    while (!s.isEmpty()) {
        Integer top = s.pop();
        count++;
        // 所有后继入度-1
        for (int i = 0; i < numCourses; i++) {
            if (top!=i&&matrix[top][i] == 1) {
                indegree[i]--;
                if (indegree[i] == 0) {//入度减为0 没有前驱了  可以去学习啦
                    s.push(i);
                }
            }
        }
    }
    return count == numCourses;//都学过才行
}

好久没写了，效率好低啊。接下来，看题解优化一下：

改成邻接表试试，哇塞，快了5倍欸

时间空间都节省了：
在这里插入图片描述

// 经典拓扑排序
public boolean canFinish(int numCourses, int[][] prerequisites) {
    int[] indegree = new int[numCourses];
    ArrayList<ArrayList<Integer>> list = new ArrayList<>();//邻接表

    for (int i = 0; i < numCourses; i++) {
        list.add(new ArrayList<Integer>());
    }

    // 领接矩阵
    for (int i = 0; i < prerequisites.length; i++) {
        int a = prerequisites[i][0], b = prerequisites[i][1];
        list.get(b).add(a);//b->a   //邻接表 同时也是hash表
        indegree[a]++; // 随便记录每个元素的入度
    }

    Stack<Integer> s = new Stack<>();
    for (int i = 0; i < numCourses; i++) {
        if (indegree[i] == 0) s.push(i);
    }

    int count = 0;
    while (!s.isEmpty()) {
        Integer top = s.pop();
        count++;
        // 所有后继入度-1 //邻接表直接能找到
        for (Integer e : list.get(top)) {
            if(--indegree[e]==0){
                s.push(e);
            }
        }
    }
    return count == numCourses;//都学过才行
}

208. 实现 Trie (前缀树)

老规矩，先暴力通过

每次缓存所有前缀，牺牲维护的时间，以及全局的空间

class Trie {
    HashMap<String,Integer> hash;//1存在(也算一种前缀)  2前缀
    public Trie() {
        hash = new HashMap<String,Integer>();
    }
    public void insert(String word) {
        hash.put(word,1);
        for (int i = 1; i < word.length(); i++) {
            String prefix = word.substring(0, i);
            if(!search(prefix)&&!startsWith(prefix)) hash.put(prefix,2);//所有前缀设置为2  (已经为1的不能退化为2  已经是前缀的也不需要重复put了)
        }
    }
    public boolean search(String word) {
        Integer x = hash.get(word);
        return x!=null && (x==1);
    }
    public boolean startsWith(String prefix) {
        Integer x = hash.get(prefix);
        return x!=null && (x==1||x==2);//存在也算前缀
    }
}

class Trie2 {

    Set<String> set = new HashSet<>();
    public Trie2() {}

    public void insert(String word) {
        set.add(word);
    }

    public boolean search(String word) {
        return set.contains(word);
    }

    public boolean startsWith(String prefix) {
        if(set.contains(prefix)) return true;
        for (String s : set) {
            if(s.startsWith(prefix)) return true;
        }
        return false;
    }
}

其实你想想jdk1.7 ConcurrentHashMap，可不可以类似地直接一个用一个长度为26的大数组，首字母作为key, 每个大数组下面若干小数组，每个小数组又可以拉链，似乎真的可以

但本题当然没这么简单，本题是一个26叉树，每个结点都有26个成员，树构建好了，就简单了。

不要怕空间，每个结点26长的数组也不算大了，不就是26叉树吗，和二叉树没啥区别呀

核心思想：
前缀树：1、26叉树 2、结构如下

struct TrieNode {
    bool isEnd; //该结点是否是一个串的结束
    TrieNode* next[26]; //字母映射表
};

26叉树实现前缀树 tries

时间和空间上都快多了

在这里插入图片描述

class Trie {

    private Trie[] next; //下标即是对应字符  null表示没有  !null表示有
    private boolean isEnd; // 默认false


    public Trie() {// new Trie(); 才是调用构造方法创建对象
        next = new Trie[26];//真的只是创建了引用数组 只是new了数组存放引用的内存 并没有真的new对象内存
        isEnd = false;

    }
    public void insert(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            int x = word.charAt(i)-'a';
            if(node.next[x]==null){
                node.next[x] = new Trie();
            }
            node = node.next[x];
        }
        node.isEnd = true;
    }

    public boolean search(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            int x = word.charAt(i)-'a';
            if(node.next[x]==null){
                return false;
            }
            node = node.next[x];
        }
        return node.isEnd;

    }
    public boolean startsWith(String prefix) {
        Trie node = this;
        for (int i = 0; i < prefix.length(); i++) {
            int x = prefix.charAt(i)-'a';
            if(node.next[x]==null){
                return false;
            }
            node = node.next[x];
        }
        return true;

    }
}

上面两个方法有大量重复代码，其实可以抽取复用的

class Trie {

    private Trie[] next; //下标即是对应字符  null表示没有  !null表示有
    private boolean isEnd; // 默认false


    public Trie() {// new Trie(); 才是调用构造方法创建对象
        next = new Trie[26];//真的只是创建了引用数组 只是new了数组存放引用的内存 并没有真的new对象内存
        isEnd = false;

    }
    public void insert(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            int x = word.charAt(i)-'a';
            if(node.next[x]==null){
                node.next[x] = new Trie();//这是才是创建对象内存
            }
            node = node.next[x];
        }
        node.isEnd = true;
    }

    public boolean search(String word) {
        Trie trie = searchPrefix(word);
        return trie!=null && trie.isEnd;
    }
    public boolean startsWith(String prefix) {
        return searchPrefix(prefix) != null;
    }

    // 上面两个方法代码重复了 (复制粘贴固然方便 抽取通用方法 复用 才是最好的实现方式)
    public Trie searchPrefix(String prefix){
        Trie node = this;
        for (int i = 0; i < prefix.length(); i++) {
            int x = prefix.charAt(i)-'a';
            if(node.next[x]==null){
                return null;
            }
            node = node.next[x];
        }
        return node;
    }
}

★ Student[] strArr= new Student[26];//真的只是创建了引用数组只是new了数组存放引用的内存并没有真的new对象内存

215. 数组中的第K个最大元素

自己的思路，只有快速选择算法了，放缩法能证明<c*n c是常数 2或者3
是O(n)

类似快排写一个快速选择算法

// 类似快排 写一个快速选择算法
public int findKthLargest(int[] nums, int k) {
    return findKthLargest(nums,0,nums.length-1,k-1);
}

// 类似快排 写一个快速选择算法
public int findKthLargest(int[] nums, int l,int h,int k) {
    int povit = quickSelect(nums,l,h);
    if(povit==k) return nums[povit];
    else if(povit < k) return findKthLargest(nums,povit+1,h,k);
    else return findKthLargest(nums,l,povit-1,k);
}

public int quickSelect(int[] nums, int l,int h){
    int provit = nums[l];
    while (l<h){
        while (l < h&&nums[h]<=provit) h--;
        nums[l] = nums[h];
        while (l<h&&nums[l]>provit) l++;
        nums[h] = nums[l];
    }
    nums[l]=provit;
    return l;
}

还有一处可以优化, 就是划分基准，上面的写法总是默认第一个，其实每次随机选择一个，这里测试的速度显示，会快2~3倍
随机选择一个作为基准没那么复杂，就是每次随机在范围内挑选一个元素，然后和nums[l]进行交换即可，也就是把他交换到数组开头即可。

划分的基准每次随机选择

Random random = new Random();

// 类似快排 写一个快速选择算法
public int findKthLargest(int[] nums, int k) {
    return findKthLargest(nums,0,nums.length-1,k-1);
}

// 类似快排 写一个快速选择算法
public int findKthLargest(int[] nums, int l,int h,int k) {
    int povit = quickSelect(nums,l,h);
    if(povit==k) return nums[povit];
    else if(povit < k) return findKthLargest(nums,povit+1,h,k);
    else return findKthLargest(nums,l,povit-1,k);
}

public int quickSelect(int[] nums, int l,int h){
    int provit = random.nextInt(h - l + 1) + l;
    swap(nums,l,provit);//随机选择一个作为基准 换到l的位置 才能进行快排的划分呐
    int tmp = nums[l];
    while (l<h){
        while (l < h&&nums[h]<=tmp) h--;
        nums[l] = nums[h];
        while (l<h&&nums[l]>tmp) l++;
        nums[h] = nums[l];
    }
    nums[l]=tmp;
    return l;
}

void swap(int[] nums, int a,int b){
    int tmp = nums[a];
    nums[a] = nums[b];
    nums[b] = tmp;
}

堆排序时间复杂度O(nlogn)

221. 最大正方形

直接暴力，果然超时了 (差3组没过)

猜想因该是dp

然后在暴力的基础上进行了剪枝，竟然过了

public int maximalSquare(char[][] matrix) {
    int max = 0;
    for (int i = 0; i < matrix.length; i++) {
        if(matrix.length-i<max) break; //不必要了验证了
        for (int j = 0; j < matrix[i].length; j++) {
            int d = max; //不必要的验证就不用做了 直接找找看有没有更大的
            while (judge(matrix,i,j,d)) d++; //后面也不需要验证了
            max = Math.max(max,d);
        }
    }
    return max*max;
}

boolean judge(char[][] matrix, int x, int y, int d) {
    if(x+d>=matrix.length||y+d>=matrix[0].length) return false;
    for (int i = x; i <= x + d; i++) {
        for (int j = y; j <= y + d; j++) {
            if (matrix[i][j] == '0') return false;//千万注意是跟字符'0'做比较
        }
    }
    return true;
}

这种写法空间上非常优秀，但是时间上还是很慢

dp 状态转移方程可以找规律的

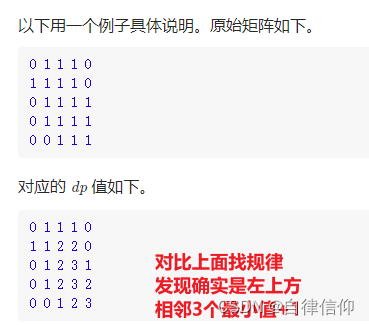
在这里插入图片描述

仔细想想确实这样，因为三个相邻点的值一定都>=他们3的最小值

改用dp，慢慢优化，最后如下：

public int maximalSquare(char[][] matrix) {
    if (matrix == null || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) return 0;
    int m = matrix.length, n = matrix[0].length;
    int[][] dp = new int[m][n];
    int max = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if(matrix[i][j] == '1'){//=='0'不需要处理 因为默认值就是0 节省一点
                if (i < 1 || j < 1) dp[i][j] = 1;
                else dp[i][j] = Math.min(dp[i-1][j], Math.min(dp[i][j-1], dp[i-1][j-1])) + 1;
            }
            max = Math.max(max, dp[i][j]);
        }
    }
    return max*max;
}

题解看到一种二进制做法，很巧妙，可惜时间反而更长了

输入数据1 <= m, n <= 300 所以每行最多300位，long long 也承受不了这么长的二进制，不能直接&，除非大数
自己循环写&,就慢了所以这种方式不是很好，python天然就是大数，所以不用考虑这个问题，但是python更慢

不考虑溢出的写法如下，不能完全通过。这个方法看起来很妙，其实没有那么可行

public int maximalSquare(char[][] matrix) {
    int max = 0;
    int[] nums = new int[matrix.length];
    for (int i = 0; i < matrix.length; i++) {
        int num = 0;
        for (int j = 0; j < matrix[i].length; j++) {
            num = (num<<1) + (matrix[i][j]-'0');
        }
        nums[i] = num;
    }

    for (int i = 0; i < nums.length; i++) {
        //System.out.print(nums[i]+" ");
        int sum = nums[i];
        for(int j =i;j<nums.length;j++){
            sum &= nums[j];//注意累加地& 各种组合都要遍历到
            if(getOne(sum)<j-i+1) break;;
            max = Math.max(max, j-i+1);
        }
    }
    return max*max;
}

int getOne(int num){
    int k = 0;
    while (num>0){
        num = (num<<1)&num;
        k++;
    }
    return k;//最多有几个连续的1
}

226. 翻转二叉树

确实有点水了

public TreeNode invertTree(TreeNode root) {
    if(root==null) return null;

    invertTree(root.left);
    invertTree(root.right);

    TreeNode tmp = root.left;
    root.left = root.right;
    root.right = tmp;

    return root;
}

更牛的写法

public TreeNode invertTree(TreeNode root) {
    if(root==null) return null;

    TreeNode left = invertTree(root.left);
    TreeNode right = invertTree(root.right);

    root.left = right;
    root.right = left;

    return root;
}

234. 回文链表

节省空间O(1), 且时间O(n)

头插法反转后半部分，然后和前半部分一一比较即可

public boolean isPalindrome(ListNode head) {
    ListNode root = new ListNode();

    int k = 0;
    ListNode node = head;
    while (node != null) {
        node = node.next;
        k++;
    }

    int T = k / 2;
    node = head;
    while (T-- > 0) node = node.next;

    if (k % 2 != 0) node = node.next; // 奇数要去掉一个

    // 逆置后半段
    while (node != null) {
        // 先摘下来
        ListNode t = node;
        node = node.next;

        // 再头插法逆置
        t.next = root.next;
        root.next = t;
    }

    // 再做比较
    ListNode l1 = root.next, l2 = head;
    while (l1 != null) {
        if (l1.val != l2.val) return false;
        l1 = l1.next;
        l2 = l2.next;
    }

    return true;
}

236. 二叉树的最近公共祖先

// 先直接BFS找路径吧
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    ArrayList<TreeNode> path1 = dfs(root,p,new ArrayList<TreeNode>());//拿到全路径
    ArrayList<TreeNode> path2 = dfs(root,q,new ArrayList<TreeNode>());
    // 末尾填充1个null 简化比较的逻辑
    path1.add(null);
    path2.add(null);
    for(int i=0;i<path1.size();i++){
        if(path1.get(i)!=path2.get(i)) return path1.get(i-1);
    }
    return null;
}

ArrayList<TreeNode> dfs(TreeNode root,TreeNode p ,ArrayList<TreeNode> list){
    if(root==null) return null;
    list.add(root);
    if(root==p) return new ArrayList<TreeNode>(list);//最后新复制一份返回 防止list退栈后又没了

    ArrayList<TreeNode> left = dfs(root.left,p,list);
    if(left!=null) return left;
    ArrayList<TreeNode> right = dfs(root.right,p,list);
    if(right!=null) return right;

    list.remove(root);//退栈时去掉
    return null;
}

题解有一个有趣的做法，后续遍历查找有无p,q 途中根据左右子树有无p,q就可以判断出结果了

p,q是两个独一无二的结点
左右都返回true，一定一个是有p，另一个有q

// 先直接BFS找路径吧
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    dfs(root, p, q);
    return ans;
}

TreeNode ans;
boolean dfs(TreeNode root,TreeNode p ,TreeNode q){
    if(root==null) return false;

    boolean lson = dfs(root.left,p,q);
    boolean rson = dfs(root.right,p,q);

    //System.out.println(root.val+" "+lson+" "+ rson);

    // 后续遍历 保证了最深 （不看这两个if 就是单纯判断有无p或者q的代码）
    if(lson&&rson) {
        ans = root;
        return true; // 左右各一个 我就是公共祖先
    }

    // 我是p或者q 我下面有另一个结点  那么我就是最近公共
    if((lson||rson)&&(root==p||root==q)) {
        ans = root;
        return true;
    }
    // lson||rson 很重要 左边有 或者右边右 上面就全部返回true  这里有点难
    return lson||rson||root==p||root==q; // 自己不是p或者q但是 左右子树 有p或者q 那么我就是有
}

238. 除自身以外数组的乘积

在这里插入图片描述

// 二刷还是 不会 关键是要想到计算前后缀呀 (画一个矩阵  每行就是输入数组 对角线全部置为1 然后计算前后缀就简单了)
public int[] productExceptSelf(int[] nums) {
    // 前缀
    int[] prefix = new int[nums.length];
    prefix[0] = 1;
    for (int i = 0; i < nums.length - 1; i++) {
        prefix[i + 1] = prefix[i] * nums[i];
    }

    // 后缀
    int[] suffix = new int[nums.length];
    suffix[nums.length - 1] = 1;
    for (int i = nums.length - 1; i > 0; i--) {
        suffix[i-1] = suffix[i] * nums[i];
    }


    int[] ans = new int[nums.length];
    for (int i = 0; i < ans.length; i++) {
        ans[i] = prefix[i] * suffix[i];
    }

    return ans;
}

节省空间很容易优化了：

// 二刷还是 不会 关键是要想到计算前后缀呀 (画一个矩阵  每行就是输入数组 对角线全部置为1 然后计算前后缀就简单了)
public int[] productExceptSelf(int[] nums) {
    // 前缀
    int[] prefix = new int[nums.length];
    prefix[0] = 1;
    for (int i = 0; i < nums.length - 1; i++) {
        prefix[i + 1] = prefix[i] * nums[i];
    }
    // 节省空间 直接乘到prefix上面即可
    int suffix= 1;
    for (int i = nums.length - 1; i > 0; i--) {
        suffix *= nums[i];
        prefix[i-1] *= suffix;
    }
    return prefix;
}

240. 搜索二维矩阵 II

剑指里面刷过，所以这里还记得，就很简单了，关键点在于，从左下角开始搜索

// 技巧 从左下角开始搜索
public boolean searchMatrix(int[][] matrix, int target) {
    int m = matrix.length,n=matrix[0].length;
    int i=m-1,j=0;
    while (matrix[i][j]!=target){
        if(matrix[i][j] > target) i--;
        else j++;
        if(i<0||j>=n) return false;
    }
    return true;
}

279. 完全平方数

dp 效率有点低啊

// dp的题目比较难 可能就不需要考虑效率
public int numSquares(int n) {
    int[] dp = new int[n+1];
    for(int i=1;i<=n;i++){
        int min = Integer.MAX_VALUE;
        for(int j=1;j<=Math.sqrt(i);j++){
            min = Math.min(dp[i-j*j],min);//每个可能的平方数都试一次 开始不要考略效率，可能最有效率就不是很好呢
        }//然后这里的最优子结构 用得非常好
        dp[i] = min+1;
    }
    return dp[n];
}

下面想办法提升一下效率

看题解发现，原来还有一个更牛的做法，纯数学定理解决此问题

在这里插入图片描述

四平方和定理

// 四平方和定理 更牛
public int numSquares(int n) {
    if(isOne(n)) return 1;
    if(isTwo(n)) return 2;
    if(isFour(n)) return 4;
    return 3;//3不好判断，但是只剩下他了
}

boolean isOne(int n){
    int k = (int) Math.sqrt(n);
    return k*k==n;
}

boolean isTwo(int n){
    for (int i = 1; i <= Math.sqrt(n); i++) {
        if(isOne(n-i*i)) return true;
    }
    return false;
}

boolean isFour(int n) {
    while (n%4==0) n/=4;
    return n%8==7;
}

这也太快了点吧
在这里插入图片描述

283. 移动零

方法1，先暴力（冒泡排序）

// 暴力冒泡排序
public void moveZeroes(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        boolean flag = false;
        for(int j=0;j<nums.length-i-1;j++){
            if(nums[j] == 0){
                int t=nums[j+1];
                nums[j+1]=nums[j];
                nums[j]=t;
                flag = true;
            }
        }
        if(!flag) break;
    }
}

方法2：个人觉得还不错，直接搜集非0，后面的全部填充0，没有交换，直接覆盖

// 直接重新收集非0 直接覆盖 O(n)
public void moveZeroes(int[] nums) {
    int k =0;
    for (int i = 0; i < nums.length; i++) {
        if(nums[i]!=0) nums[k++]=nums[i];
    }
    for(int i=k;i<nums.length;i++) nums[i]=0;
}

方法3：题解方法：双指针，也不错，真的在交换

// 直接重新收取非0 直接覆盖 O(n)
public void moveZeroes(int[] nums) {
    int k =0;
    for (int i = 0; i < nums.length; i++) {
        if(nums[i]!=0) nums[k++]=nums[i];
    }
    for(int i=k;i<nums.length;i++) nums[i]=0;
}

287. 寻找重复数

必须不修改数组 nums 且只用常量级 O(1) 的额外空间。

题解里好多大神:
个人觉得这两种写法比较好:
1: 转换为：找链表中环的起点问题
2: 范围1~n 可以将每个数字看成指针，对应位置取相反数
某个位置已经被修改为负数了就直接退出
然后再重复取一次相反数就还原了

两种解法相同的关键点：范围1~n 可以将每个数字看成指针

1. 找链表中环的起点问题

public int findDuplicate(int[] nums) {
    int fast=0,slow=0;
    do{
        slow = nums[slow];
        fast = nums[nums[fast]];
    }while (slow!=fast);//后验 用do while
    slow = 0;
    while (fast!=slow){
        slow = nums[slow];
        fast = nums[fast];
    }
    return slow;
}

1. 对应位置取相反数

public int findDuplicate(int[] nums) {
    int res=-1;
    for (int i = 0; i < nums.length; i++) {
        int k = Math.abs(nums[i]);//nums[i]一旦重复 必然给同一个位置 乘上至少2次-1
        if(nums[k]<0){
            res = k;
            break;
        }else {
            nums[k]*=-1;//对应位置乘上-1
        }
    }

    // 不能修改原数组 还原
    for (int i = 0; i < nums.length; i++) {
        int k = Math.abs(nums[i]);//nums[i]一旦重复 必然给同一个位置 乘上至少2次-1
        if(nums[k]>0){
            break;
        }else {
            nums[k]*=-1;//对应位置乘上-1
        }
    }

    //System.out.println(Arrays.toString(nums));//确定还原了

    return res;
}

300. 最长递增子序列

经典老题，先用dp试试

public int lengthOfLIS(int[] nums) {
    int[] dp = new int[nums.length];
    dp[0]=1;
    int max = 1;

    for (int i = 1; i < nums.length; i++) {
        int maxv = 0;
        for(int j=i-1;j>=0;j--){
            if(nums[j]<nums[i]) maxv = Math.max(maxv,dp[j]);
        }
        dp[i] = maxv+1;

        max = Math.max(max,dp[i]);
    }
    return max;
}

不考虑效率的dp O（n^2） O（1）

下面看题解，来优化效率了

动态规划 + 二分查找 O（nlogn）O(1)
优化效率，维护一个tail序列数组，新元素插入数组，插入也是有讲究的，除非比tail末尾元素要大，就新加入 , 否则二分查找就是替换对应位置的元素，不要怕替换后位置不对，因为，只要没有将tail数组长度边长，就不会影响答案正确性

678129346
6
67
678
178
128
1289 (没问题这时6789确实长度是4)
1239
1234
12346

public int lengthOfLIS(int[] nums) {
    int[] tail = new int[nums.length];
    int res=0;
    for (int i = 0; i < nums.length; i++) {
        int l=0,r=res;
        // 二分找插入位置(直接覆盖 不真的插入 除非是最后一个)   其实就是找到第一个大于nums[i]的元素 替换掉他即可
        while (l<r){
            int m=(l+r)/2;
            if(nums[i]>tail[m]) l=m+1; //r初始值是res本来就是最右边的空闲下标
            else r=m;//可以覆盖
        }
        if(r==res) res++;
        tail[r] = nums[i];
        //System.out.println(Arrays.toString(tail));
    }
    return res;
}

309. 最佳买卖股票时机含冷冻期

这题的dp有3个，超级难想啊亲，直接看题解吧：

官方题解看得云里雾里
再看看大佬题解，进一步解析了一番，清晰多了

/*
0.不持股且当天没卖出,定义其最大收益dp[i][0];
1.持股,定义其最大收益dp[i][1]；
2.不持股且当天卖出了，定义其最大收益dp[i][2]；
* */
public int maxProfit(int[] prices) {
    int n = prices.length;
    int[][] dp = new int[n][3];

    //dp[0][0] = 0;//默认是0
    dp[0][1] = -prices[0];
    //dp[0][2] = 0; // 买入又卖出 当天为0  //默认是0

    for (int i = 1; i < n; i++) {
        dp[i][0] = Math.max(dp[i-1][0],dp[i-1][2]);//不持股且当天没卖出 =》  i-1天也不持股2种状态取大者
        dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);//持股: 昨天就持股  或者  昨天不持股,今天刚买入
        dp[i][2] = dp[i-1][1] + prices[i]; //昨天持股 今天卖出
    }

    return Math.max(dp[n-1][0],dp[n-1][2]);//持股的不用管 持股没用 没时间卖了都
}

322. 零钱兑换

先直接dfs，枚举，小恩小惠的剪枝也不行，仍然超时

只能类似之前dp那样，用一个数组记录下已经dfs过的状态，然后就可以大量减枝了，每个amount状态真的就只计算一次
也就是：记忆化搜索

// 不需要排序 意义不大
public int coinChange(int[] coins, int amount) {
    ans = new int[amount+1];//0下标不用
    int res = dfs(coins, amount);
    if(res==Integer.MAX_VALUE) return -1;
    else return res;
}
// 记忆化搜索
int[] ans; // ans[i]表示 总金额为i时最少硬币数
private int dfs(int[] coins, int amount) {
    if(amount<0) return Integer.MAX_VALUE;
    if(amount==0) return 0;//重要边界

    if(ans[amount]!=0) return ans[amount];//大量减枝  

    // 否则就慢慢算
    int min = Integer.MAX_VALUE;
    for (int i = 0; i < coins.length; i++) {
        int res = dfs(coins, amount - coins[i]);
        if(res<min) min=res+1;
    }
    ans[amount] = min;//记录下中间状态  记忆化搜索
    return ans[amount];
}

写完dfs再写dp就简单多了
dp速度也确实快一点

// 不需要排序 意义不大
public int coinChange(int[] coins, int amount) {
    int[] dp = new int[amount + 1];
    int MAX_VALUE = amount + 1;//最大只能是 amount，也即是 全部是1元的硬币    不需要用到Integer.MAX_VALUE
    Arrays.fill(dp, MAX_VALUE);
    dp[0] = 0;
    // 所有总金额 依次计算状态
    for (int i = 1; i <= amount; i++) {
        // 遍历所有硬币
        for (int j = 0; j < coins.length; j++) {
            if (coins[j] <= i) {
                dp[i] = Math.min(dp[i - coins[j]] + 1, dp[i]);
            }
        }
    }
    return dp[amount] >= MAX_VALUE ? -1 : dp[amount];
}

337. 打家劫舍 III

第一思路: 简单来看孩子被偷了父亲就不能再被偷了所以后序遍历试试

想到了后续遍历，但是没有想到需要同时维护两个值
想象成树型dp就好多了。难一点的dp本来就要多种状态同时转移

这个题解非常好

先看一个差一点的题解

// 记忆 或者说 缓存  (不缓存会超时)
HashMap<TreeNode, Integer> memo = new HashMap<>();

// 4 个孙子偷的钱 + 爷爷的钱 VS 两个儿子偷的钱 哪个组合钱多
public int rob(TreeNode root) {
    if (root == null) return 0;

    if(memo.get(root) != null) return memo.get(root);

    int money = root.val;//爷孙
    if (root.left != null) {
        money += rob(root.left.left) + rob(root.left.right);
    }
    if (root.right != null) {
        money += rob(root.right.left) + rob(root.right.right);
    }
    int dad = rob(root.left) + rob(root.right);//父  (也要递归获取)

    // 记忆
    int max = Math.max(money, dad);
    memo.put(root, max);

    return max;
}

树型dp

public int rob(TreeNode root) {
    int[] ans = rob2(root);
    return Math.max(ans[0],ans[1]);
}

public int[] rob2(TreeNode root) {
    if(root==null) return new int[]{0,0};

    int[] left = rob2(root.left);
    int[] right = rob2(root.right);//一次后续遍历  不会重复遍历节点  (相当于一次遍历同时维护两个dp数组)

    int[] ans = new int[2];
    ans[1] = root.val + left[0] + right[0];//本节点偷了  两个孩子都不能偷了
    ans[0] = Math.max(left[0], left[1]) + Math.max(right[0],right[1]);// 本结点不偷 孩子偷不偷都无妨 取最大

    return ans;
}

惊人:0ms

树的动态规划，得有这个意识了！！！！

最最后批判一下我自己的垃圾写法

直接用先序遍历，需要缓存
先序遍历每个节点有两种状态，缓存也得缓存2份
实在是太拉了

// 简单来看 孩子被偷了 父亲就不能再被偷了  所以后序遍历试试
// 不行，还是先序遍历吧 因为父亲可以选择偷还是不偷  然后 可以选择偷不偷孩子
public int rob(TreeNode root) {
    return Math.max(rob(root, true), rob(root, false));
}

// 超时了 加一个缓存吧
HashMap<TreeNode, Integer> memo1 = new HashMap<>();
HashMap<TreeNode, Integer> memo2 = new HashMap<>();

// boolean canStolen 记录下当前结点是否可以偷
public int rob(TreeNode root, boolean canStolen) {
    if (root == null) return 0;

    if (canStolen && memo1.get(root) != null) return memo1.get(root);
    if (!canStolen && memo2.get(root) != null) return memo2.get(root);

    //System.out.println(canStolen+" "+root.val);

    int sum1 = 0, sum2 = 0;
    if (canStolen) {//可以偷本结点 (说明父亲没被偷)
        sum1 += root.val;
        sum1 += rob(root.left, false);//本结点偷了 子节点 就不可以偷了
        sum1 += rob(root.right, false);
    }
    //让然不管可不可以偷本结点 我都可以选择不偷
    sum2 += rob(root.left, true);//子结点就可以偷了
    sum2 += rob(root.right, true);

    int ans = Math.max(sum1, sum2);
    if (canStolen) memo1.put(root, ans);
    if (!canStolen) memo2.put(root, ans);
    // 每个结点有两种状态 (node,true) (node,false) 缓存一种状态也不行

    return ans;
}

338. 比特位计数

我的写法，比较烂

public int[] countBits(int n) {
    int[] ans = new int[n + 1];
    for (int i = 0; i <= n; i++) {
        int k = 0;
        int num = i;
        while (num != 0) {
            k += num % 2;
            num /= 2;
            if(ans[num]!=0){
                k += ans[num];
                break;
            }
        }
        ans[i] = k;
    }
    return ans;
}

没想到，java有现成的API

public int[] countBits(int n) {
    int[] ans = new int[n+1];
    for (int i = 0; i <= n; i++) {
        ans[i] = Integer.bitCount(i);
    }
    return ans;
}

看一下源码:

@IntrinsicCandidate
public static int bitCount(int i) {
    // HD, Figure 5-2
    i = i - ((i >>> 1) & 0x55555555);
    i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
    i = (i + (i >>> 4)) & 0x0f0f0f0f;
    i = i + (i >>> 8);
    i = i + (i >>> 16);
    return i & 0x3f;
}

看不懂

题解好多种dp，个人觉得最牛的dp还是这一版

public int[] countBits(int n) {
    int[] ans = new int[n+1];
    for (int i = 1; i <= n; i++) {
        if(i%2==0) ans[i] = ans[i/2];//左移一位 末尾添0  不增加1的个数
        else ans[i] = ans[i-1] + 1; //上一个奇数 末尾+1
    }//正儿八经的O(n)形式的dp
    return ans;
}

更进一步，奇偶都不需要要讨论了，直接右移，转换为已知，末尾是1就加上

public int[] countBits(int n) {
    int[] ans = new int[n+1];
    for (int i = 1; i <= n; i++) {
        ans[i] = ans[i>>1] + (i&1); //右移动+末位加上舍弃的数字
    }
    return ans;
}

347. 前 K 个高频元素

先用Hash+堆排序直接套一波。时间O(nlogn) 空间O(distinct(nums))

public int[] topKFrequent(int[] nums, int k) {
    HashMap<Integer, Integer> map = new HashMap<>();
    for (int num : nums) {
        Integer v = map.getOrDefault(num, 0);
        map.put(num,v+1);
    }

    // 根据value(也就是出现频率)  降序排序
    PriorityQueue<Map.Entry<Integer, Integer>> pq = new PriorityQueue<>((a,b)->b.getValue()-a.getValue());

    for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
        pq.offer(entry);//优先队列自动堆排序
    }

    int[] ans = new int[k];
    for (int i = 0; i < ans.length; i++) {
        ans[i] = pq.poll().getKey();
    }

    return ans;
}

但是题目要求的是由于O(nlogn), 这个时候想想，堆不正适合找最大(或者最小)的k个数么，选择性地将k个元素放入堆中即可
最大的k个数，也就是建立小顶堆，先直接入堆个，堆顶维护最小值，大于堆顶替换堆顶，小于直接舍弃

public int[] topKFrequent(int[] nums, int k) {
   HashMap<Integer, Integer> map = new HashMap<>();
   for (int num : nums) {
       Integer v = map.getOrDefault(num, 0);
       map.put(num,v+1);
   }

   // 小根堆 只要k个就行了
   PriorityQueue<Map.Entry<Integer, Integer>> pq = new PriorityQueue<>((a,b)->a.getValue()-b.getValue());

   for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
       if(pq.size()<k) pq.offer(entry);//优先队列自动堆排序  默认小根堆 堆顶最小
       else {
           if(entry.getValue()>pq.peek().getValue()){
               pq.poll();//舍弃堆顶
               pq.offer(entry);// 重新纳入堆顶
           }
       }
   }

   int[] ans = new int[k];
   for (int i = 0; i < ans.length; i++) {
       ans[i] = pq.poll().getKey();
   }

   return ans;
}

感觉测试用例有问题，效率并没有怎么提升。代码还复杂了不少

394. 字符串解码

括号匹配，还像极了表达式求值，那不如就，用栈吧

注意字符串最左边是下标0 入栈时别弄反了

用栈还真行

// 既然是括号匹配 那就先用栈吧
public String decodeString(String s) {
    Stack<Character> stack = new Stack<>();
    for (int i = 0; i < s.length(); i++) {
        char c = s.charAt(i);
        if(c!=']'){
            stack.push(c);
        }else {
            // 中括号内的字符串-》str
            char tc;
            String str = "";
            while ((tc=stack.pop())!='[') {//最后多pop的'[' 正好丢弃
                str = tc+str;//注意字符串最左边是下标0
            }

            // 中括号前前面的整数-> ts->k
            String ts = "";
            while (!stack.isEmpty()&&Character.isDigit(stack.peek())){//不能多pop了 改用peek
                ts = stack.pop() + ts;
            }
            int k = Integer.parseInt(ts);
            //System.out.println(str+" "+ k);//bc 2

            // 栈内 压入k个str
            while (k-->0){
                for (int j = 0; j < str.length(); j++) {
                    stack.push(str.charAt(j));
                }
            }
        }
    }
    String ans = "";
    while (!stack.isEmpty()){
        ans = stack.pop() + ans;
    }
    return ans;
}

语法层面整理一下，效率竟然升高了，很迷惑

// 既然是括号匹配 那就先用栈吧
public String decodeString(String s) {
    Stack<Character> stack = new Stack<>();
    for (int i = 0; i < s.length(); i++) {
        char c = s.charAt(i);
        if (c != ']') stack.push(c);
        else {
            String str = "";
            while ((stack.peek()) != '[') str = stack.pop() + str;
            stack.pop();//'['

            String ts = "";
            while (!stack.isEmpty() && Character.isDigit(stack.peek())) ts = stack.pop() + ts;
            int k = Integer.parseInt(ts);

            while (k-- > 0)
                for (int j = 0; j < str.length(); j++) stack.push(str.charAt(j));
        }
    }
    String ans = "";
    while (!stack.isEmpty()) ans = stack.pop() + ans;
    return ans;
}

题解大思路跟我差不多，细节上有所不同，题解用的不定长数组LinkedList模拟的栈，遍历时要快一点而已，综合要快2ms

406. 根据身高重建队列

官解太麻烦了，有个简单解法

在这里插入图片描述

public int[][] reconstructQueue(int[][] people) {
    LinkedList<int[]> list = new LinkedList<>();
    Arrays.sort(people, new Comparator<int[]>() {
        @Override
        public int compare(int[] o1, int[] o2) {
            if(o1[0]!=o2[0]) return o2[0]-o1[0];
            else return o1[1]-o2[1];
        }
    });
    for (int[] person : people) {
        list.add(person[1],person);
    }
    return list.toArray(new int[0][]);
}

416. 分割等和子集

全部样例都通过，然后还报超时，也是没谁了

// 总和是定的 是否加起来=1半就行了
public boolean canPartition(int[] nums) {
    int target = Arrays.stream(nums).sum();
    if(target%2==0) target /=2;
    else return false;
    dfs(nums,0,target);//接下来就是看数组种是否有某个子集的和为target了 转化成了之前的dfs问题
    return flag;
}

boolean flag = false;
HashMap<String, Boolean> map = new HashMap<String, Boolean>();//减枝
boolean dfs(int[] nums,int n,int target){
    if(target<0||n>=nums.length) return false;
    if(target==0||flag) return true;

    if(map.containsKey(n+"-"+target)) return map.get(n+"-"+target);

    // 选或者不选2种情况
    boolean b = dfs(nums,n+1,target) || dfs(nums,n+1,target-nums[n]);
    map.put(n+"-"+target,b);
    if(b) flag = b;
    return b;
}

只能转换成非递归形式，也就是dp来做了

仔细想想，不就是0-1背包吗？这里没有权重限制，只要拿或者不拿，能偷到恰好target的物品即可。
先用二维数组写，再优化为一维滚动数组

注意滚动数组这里得倒过来遍历否则前面的会覆盖后面的

public boolean canPartition(int[] nums) {
    int target = Arrays.stream(nums).sum();
    if(target%2==0) target /=2;
    else return false;

    boolean[] dp = new boolean[target+1];
    dp[0] = true;
    if(nums[0]<=target) dp[nums[0]] = true;//也是边界  // 第0次的dp
    // 其他默认false

    for(int i = 1; i < nums.length; i++){
        for (int j = target; j >= 1; j--) {//注意滚动数组这里得倒过来遍历 否则前面的会覆盖后面的
            if(j>=nums[i]){//第i个不能拿
                dp[j] = dp[j]|dp[j-nums[i]];
            }
        }
    }
    return dp[target];
}

437. 路径总和 III

虽然之前在剑指里刷过，但是二刷还是不会，细节，还有反复多次，真的很重要。
时间不够时，就要特别注重方法

最简单的思路：两次先序遍历，第一次确定起点，第二次dfs找路径，就这么简单
每次定死一个起点，绝对不会有重复的起点到每个结点都只算了一次
if(targetSum-root.val==0) 先减了root.val才是访问了该结点，才是先序。否则if(targetSum==0) 并不是先序，根本就是错的

还有就是要注意一个坑爹的测试用例：[1000000000,1000000000,null,294967296,null,1000000000,null,1000000000,null,1000000000]
Integer溢出之后正好变成了0，所以dfs里的targetSum要改成Long类型

public int pathSum(TreeNode root, int targetSum) {
    if(root==null) return 0;
    dfs(root, (long) targetSum);//先序遍历确定起点
    pathSum(root.left,targetSum);
    pathSum(root.right,targetSum);
    return count;
}

int count=0;
public void dfs(TreeNode root, Long targetSum) {
    if (root == null) return;
    if(targetSum-root.val==0) count++;//-root.val才表示先序访问了这个结点
    //先序遍历 一定得先减     所以千万注意这里是targetSum-root.val==0而不是targetSum==0否则就不是先序遍历了
    dfs(root.left, targetSum-root.val);
    dfs(root.right, targetSum-root.val);
}

用map记录前缀和，飞快

在这里插入图片描述
前缀和，太牛了~

public int pathSum(TreeNode root, int targetSum) {
    HashMap<Long, Integer> prex = new HashMap<>();
    prex.put(0L,1);//很重要 否则起点正好是根root的路径就会被遗漏
    dfs(root, (long) targetSum,0l,prex);
    return count;
}

int count=0;
public void dfs(TreeNode root, Long targetSum, Long curr, HashMap<Long,Integer> prex) {
    if (root == null) return;

    curr += root.val;

    count += prex.getOrDefault(curr-targetSum,0);
    prex.put(curr,prex.getOrDefault(curr,0)+1);

    dfs(root.left, targetSum,curr,prex);
    dfs(root.right, targetSum,curr,prex);

    // 退栈时清除当前结点
    prex.put(curr,prex.getOrDefault(curr,0)-1);
}

438. 找到字符串中所有字母异位词

自己尝试滑动窗口，艰难地通过了
类似kmp，但是这里引出了距离的概念，2个串之间的距离，为 p-s.sub 的差集长度

public List<Integer> findAnagrams(String s, String p) {
    ArrayList<Integer> ans = new ArrayList<>();
    if(s.length()<p.length()) return ans;

    HashMap<Character, Integer> mapp = new HashMap<>();
    HashMap<Character, Integer> mapsub = new HashMap<>();
    int d = p.length();
    int l=0,r=d-1;

    // 死Hash
    for (int i = 0; i < d; i++) {
        mapp.put(p.charAt(i),mapp.getOrDefault(p.charAt(i),0)+1);
    }

    // 动态Hash
    for (int i = l; i <= r; i++) {
        mapsub.put(s.charAt(i),mapsub.getOrDefault(s.charAt(i),0)+1);
    }

    while (l<=r&&r<s.length()){
        int t = distance(mapp,mapsub);
        if(t==0) {
            ans.add(l);
            //System.out.println(s.substring(l,r+1));
            mapsub.put(s.charAt(l),mapsub.get(s.charAt(l))-1);
            l++;r++;
            if(r>=s.length()) break;
            mapsub.put(s.charAt(r),mapsub.getOrDefault(s.charAt(r),0)+1);
        }
        else {
            while (t-->0){
                mapsub.put(s.charAt(l),mapsub.get(s.charAt(l))-1);
                l++;
                r++;
                if(r>=s.length()) break;
                mapsub.put(s.charAt(r),mapsub.getOrDefault(s.charAt(r),0)+1);
            }
        }
    }
    return ans;
}

public int distance(HashMap<Character, Integer> map1,HashMap<Character, Integer> map2){
    int dis = 0;
    for (Character c : map1.keySet()) {
        int n1 = map1.get(c);
        int n2 = map2.getOrDefault(c,0);
        dis += n2>=n1?0:n1-n2;
    }
    return dis;
}

语法层面优化一下代码：

优化1：

public void put(HashMap<Character, Integer> map,String s){
    for (char c : s.toCharArray()) {
        put(map, c,1);
    }
}

public void put(HashMap<Character, Integer> map,char c,int v){//原来基础上+v
    map.put(c, map.getOrDefault(c,0)+v);
}

public List<Integer> findAnagrams(String s, String p) {
    ArrayList<Integer> ans = new ArrayList<>();
    if (s.length() < p.length()) return ans;

    HashMap<Character, Integer> mapp = new HashMap<>();
    HashMap<Character, Integer> mapsub = new HashMap<>();
    int l = 0, r = p.length() - 1;

    // 死Hash
    put(mapp,p);
    // 动态Hash
    put(mapsub,s.substring(l,r+1));

    while (l <= r && r < s.length()) {
        int t = distance(mapp, mapsub);
        if (t == 0) {
            ans.add(l);
            put(mapsub,s.charAt(l++),-1);
            if (++r>= s.length()) break;
            put(mapsub,s.charAt(r),1);
        } else {
            while (t-- > 0) {
                put(mapsub,s.charAt(l++),-1);
                if (++r >= s.length()) break;
                put(mapsub,s.charAt(r),1);
            }
        }
    }
    return ans;
}

public int distance(HashMap<Character, Integer> map1, HashMap<Character, Integer> map2) {
    int dis = 0;
    for (Character c : map1.keySet()) {
        int n1 = map1.get(c);
        int n2 = map2.getOrDefault(c, 0);
        dis += n2 >= n1 ? 0 : n1 - n2;
    }
    return dis;
}

优化2：只会出现小写字母，直接Hash = new int[26] 不就行了

public List<Integer> findAnagrams(String s, String p) {
    ArrayList<Integer> ans = new ArrayList<>();
    if (s.length() < p.length()) return ans;

    int[] hashP = new int[26];
    int[] hashS = new int[26];
    int l = 0, r = p.length();//左闭右开

    for (char c : p.toCharArray()) {
        hashP[c - 'a']++;
    }
    for (char c : s.substring(0, r).toCharArray()) {
        hashS[c - 'a']++;
    }

    while (l < r && r <= s.length()) {//[l,r) 左闭右开
        // 计算距离
        int dis = 0;
        for (int i = 0; i < 26; i++) {
            if (hashP[i] > hashS[i]) dis += hashP[i] - hashS[i];
        }
        if (dis == 0) {
            ans.add(l);
            hashS[s.charAt(l++)-'a']--;
            if (r >= s.length()) break;
            hashS[s.charAt(r++)-'a']++;
        } else {
            while (dis-- > 0) {
                hashS[s.charAt(l++)-'a']--;
                if (r >= s.length()) break;
                hashS[s.charAt(r++)-'a']++;
            }
        }
    }
    return ans;
}

快了不是一点点呀，简直了
在这里插入图片描述

思路完全正确，和题解几乎一样，但是其实还可以进一步优化的
看了题解进一步优化，直接维护一个differ数组即可（计算differ模块就从O(26)变O(1)，也还行)。先不写了

448. 找到所有数组中消失的数字

老规矩，先空间上暴力求解一下，时间上几乎无敌，空间就很拉

public List<Integer> findDisappearedNumbers(int[] nums) {
    ArrayList<Integer> ans = new ArrayList<>();
    int[] hash = new int[nums.length + 1];
    for (int num : nums)  hash[num]=1;
    for (int i = 1; i < hash.length; i++) if(hash[i] == 0) ans.add(i);
    return ans;
}

接下来再考虑如何优化空间

public List<Integer> findDisappearedNumbers(int[] nums) {
    ArrayList<Integer> ans = new ArrayList<>();
    int n = nums.length;
    // 修改原数组
    for (int i = 0; i < n; i++) {
        nums[nums[i]%n] += n;
    }
    for (int i = 0; i < n; i++) {
        if(nums[i]<=n) ans.add(i==0?n:i);//<=n也是不存在  严格>n才是存在  因为本来值的范围在[1,n]
    }
    return ans;
}

看起来节省了空间，但是实际执行，效果却并不明显

461. 汉明距离

异或之后的那个数中1的个数就是，于是转换为 338.比特位计数

java自带的API可以O(1)的复杂度求bitCount

public int hammingDistance(int x, int y) {
    return Integer.bitCount(x^y);//API O(1)的解法
}

494. 目标和

先dfs暴力搜索一下，能通过即可

public int findTargetSumWays(int[] nums, int target) {
    dfs(nums,0,target);
    return count;
}
int count = 0;
void dfs(int[] nums,int n,int target){
    if(target==0&&n==nums.length) count++;
    if(n>=nums.length) return;
    dfs(nums,n+1,target-nums[n]);//-号
    dfs(nums,n+1,target+nums[n]);//+号
}

可以简化一下:

public int findTargetSumWays(int[] nums, int target) {
    return dfs(nums,0,target);
}
int dfs(int[] nums,int n,int target){
    if(target==0&&n==nums.length) return 1;
    if(n>=nums.length) return 0;
    return dfs(nums,n+1,target-nums[n])+dfs(nums,n+1,target+nums[n]);
}

dfs优化，肯定得写dp了，感觉好麻烦啊
看题解吧

哎呀，原来就是背包问题啊，这么一想，也不难嘛

不过细节上还是很烦人的,主要是平移操作(下标不能为负数啊)

public int findTargetSumWays(int[] nums, int target) {
    // 注意 中间的target可以出现负数 但是下标不能是负数啊 只得平移一下了
    // 用sum平移: 0 <= nums[i] <= 1000 都是正的用sum平移正好
    // 本来  -sum<=j<=sum  ==现在==>  0<=j<=2*sum
    int sum = Arrays.stream(nums).sum();
    if (Math.abs(target) > sum) return 0;//绝对值超过sum绝对无解 不需要考虑

    //dp[i][j] nums[0~i]值为j的表达式的个数 (这样容纳了所有dfs的情况 还不用递归)
    int N = 2 * sum + 1; //下标 [0~2*sum]
    int[][] dp = new int[nums.length][N];

    // 初始化边界很重要 //下面有i-1 所以得从i=1开始优化  0就单独作为边界初始化一下吧
    // i==0 只有两种状态为1   dp[0][nums[0]]=1和dp[0][-nums[0]]=1
    //             平移后就是dp[0][sum+nums[0]]=1和dp[0][sum-nums[0]]=1
    dp[0][sum + nums[0]]++;
    dp[0][sum - nums[0]]++;//++是为了防止 nums[0]==0   确实+nums[0]和-nums[0] 两个表达式值都为j

    for (int i = 1; i < nums.length; i++) {
        for (int j = 0; j < N; j++) {
            // dp[0][0~2*sum]都以及初始化好了 下面直接状态转移就行了
            int a = j - nums[i] >= 0 ? j - nums[i] : 0;
            int b = j + nums[i] < N ? j + nums[i] : 0;
            dp[i][j] = dp[i - 1][a] + dp[i - 1][b];
        }
    }
    return dp[nums.length - 1][sum+target];//注意目标值平移target
}

这还没法优化成滚动数组，因为j+nums[i],j-nums[i]前后都要用就先这样吧

538. 把二叉搜索树转换为累加树

感觉有点简单啊

典型的"后序"遍历 BST中序是升序所以这里应该是逆中序也就是 LNR->RNL

int pre = 0;
public TreeNode convertBST(TreeNode root) {
    if(root==null) return null;
    convertBST(root.right);
    root.val += pre;
    pre = root.val;
    convertBST(root.left);
    return root;
}

据说： Morris 遍历可以不用递归实现树的中序遍历，也就节省了空间

非递归实现中序遍历，留待后期慢慢做工作吧

543. 二叉树的直径

个人见解: 每个结点的左右子树深度之和取最大值

int max = 0;
public int diameterOfBinaryTree(TreeNode root) {
    if(root==null) return 0;
    int path = height(root.left)+height(root.right);
    max = Math.max(max, path);
    diameterOfBinaryTree(root.left);
    diameterOfBinaryTree(root.right);
    return max;
}

HashMap<TreeNode, Integer> map = new HashMap<>();//大量剪枝
int height(TreeNode root) {
    if (root == null) return 0;
    if(map.containsKey(root)) return map.get(root);
    int high =  Math.max(height(root.left), height(root.right)) + 1;
    map.put(root,high);
    return high;
}

通过了，2ms,但是显然还有更优的解法

果然可以优化：求height的过程中就可以维护max了

public int diameterOfBinaryTree(TreeNode root) {
    height(root);
    return max;
}
int max = 0;
int height(TreeNode root) {
    if (root == null) return 0;
    int left = height(root.left);
    int right = height(root.right);
    max = Math.max(max, left + right);//求height的过程中就可以 维护max呀
    return Math.max(left, right) + 1;
}