题目

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：

输入：m = 2, n = 3, k = 1
输出：3

示例 2：

输入：m = 3, n = 1, k = 0
输出：1

提示：

1 <= n,m <= 100
0 <= k <= 20

解题思路

1.题目要求我们求出机器人能够到达多少个格子，对于这道题我们依旧采用深度优先搜索来解决。

2.首先定义一个m行n列的布尔类型的visited数组，用来记录每个格子是否被访问过。然后定义一个dfs方法，用来进行深度优先搜索。在搜索过程中，如果当前格子的行或列小于0，或者大于等于m或n，或者当前格子已经被访问过，或者当前格子的数字之和大于k，则返回0。否则，将当前格子标记为已访问，并返回1加上向右、向下、向左、向上四个方向的dfs调用结果之和。

3.再定义一个sum方法，用来计算一个数字的每一位之和。首先定义一个res变量，并将其初始化为0。然后判断x是否为0，如果不为0，则将res加上x的个位数，并将x除以10。最后返回res。

4.在movingCount方法中，首先初始化类成员变量m、n和k，并创建一个m行n列的visited数组。然后调用dfs方法，从矩阵的左上角开始搜索，并返回结果。

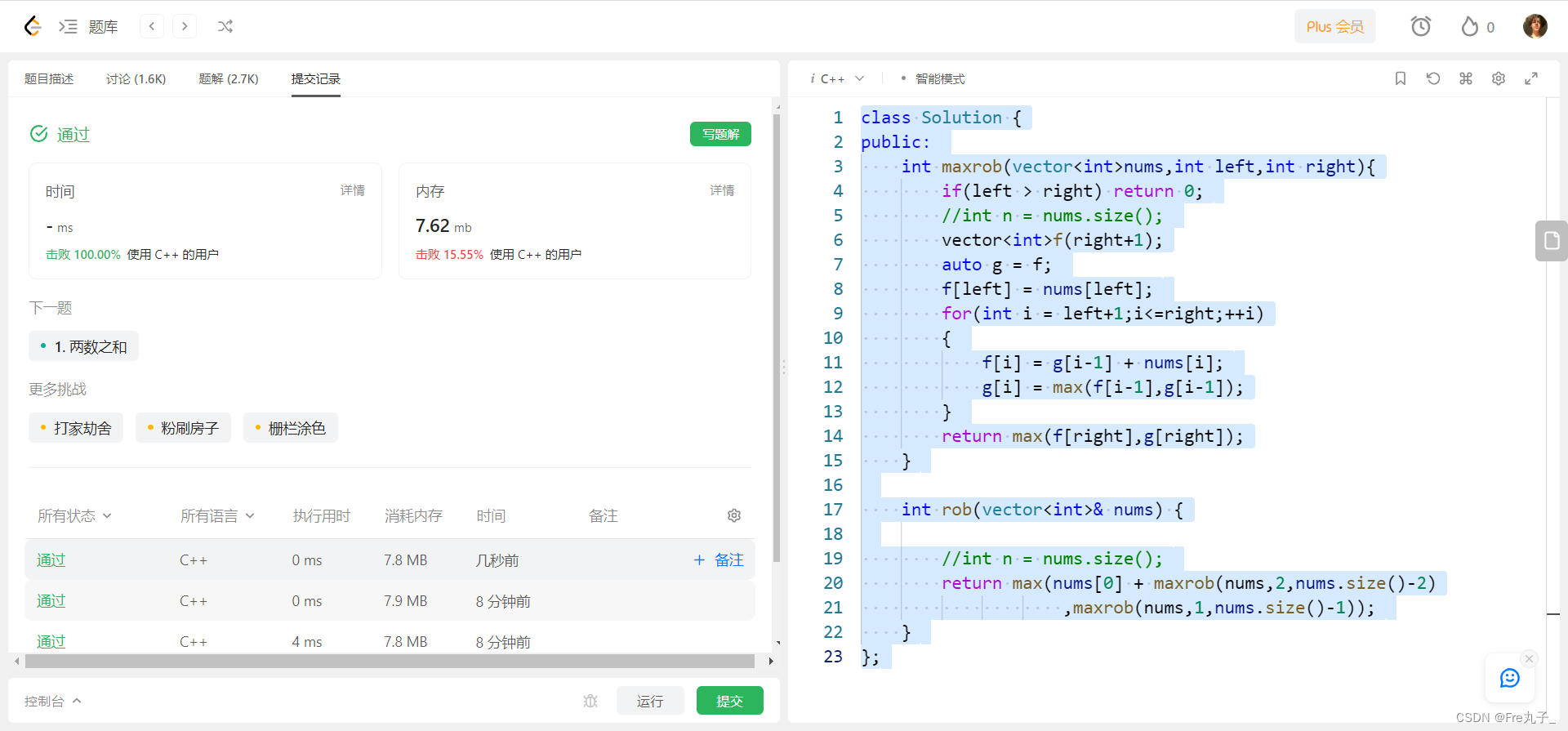
代码实现

class Solution {
    int m;
    int n;
    int k;
    boolean[][] visited;
    public int movingCount(int m, int n, int k) {
        this.m = m;
        this.n = n;
        this.k = k;
        visited = new boolean[m][n];
        return dfs(0,0);
    }
    public int dfs(int i, int j){
        if(i < 0 || j < 0 || i >= m || j >= n || visited[i][j] || k<sum(i)+sum (j)){
            return 0;
        }
        visited[i][j] = true;
        return 1 + dfs(i+1,j) + dfs(i,j+1) + dfs(i-1,j) + dfs(i,j-1);

    }
    int sum(int x){
        int res = 0;
        while(x != 0){
            res = res +(x % 10);
            x = x / 10;
        }
        return res;
    }
}