稳定性: 待排序的序列中若存在值相同的元素,经过排序之后,相等元素的先后顺序不发生改变,称为排序的稳定性。
思维导图:
(排序名称后面蓝色字体为时间复杂度和稳定性)

1.直接插入排序
核心思路
每次从无序区间中选择第一个元素,插入到有序区间的合适位置,直到整个数组有序。
排序步骤
- 定义下标 i 为当前无序区间的第一个元素, i-1 表示有序区间的最大值,下标 j 从后往前遍历有序区间。
- 有序区间:[0…i)
- 无序区间:[i…n)
- 若arr[i]>arr[i-1],直接将arr[i]纳入有序区间即可。
- 若arr[i]<arr[i-1],交换arr[i]和arr[i-1],i- -继续比较。

代码
public static void insert(int[]arr){
//有序区间:[0,i)
//无序区间:[i,n)
int n=arr.length;
//i指向当前无序区间的第一个元素
for (int i = 1; i < n; i++) {
for (int j = i; j >=1 && arr[j]<arr[j-1]; j--) {
int temp=arr[j];
arr[j]=arr[j-1];
arr[j-1]=temp;
}
}
}
优点
插入排序再近乎有序的集合上性能非常好!!!
只有当前一个元素大于后一个元素时,才需要交换,若前一个元素小于后一个元素,则不需要走第二层循环。
2.希尔排序
核心思路
希尔排序其实是对插入排序的一种优化。
先将待排序的数组分为若干个子数组。将子数组调整为有序状态,不断变大这个分组长度,当最终分组长度为1时,整个数组接近有序。最后来一次插入排序即可。
排序步骤

我们来举一个实例:
![]()
- 首先gap取5,此时相隔距离为5的元素分到了一组(一共五组,每组两个元素),然后对每一组分别进行插入排序

- gap折半为2,此时相隔距离为2的元素被分到了一组(一共两组,每组五个元素),然后对每一组分别进行插入排序

- gap再次折半为1,此时所有元素被分到了一组,对它进行插入排序,至此插入排序完成

本例中前两趟就是希尔排序的预排序,最后一趟就是希尔排序的插入排序。
代码
private static void insertionSortByGap(int[] arr, int gap) {
for (int i = gap; i < arr.length; i++) {
for (int j = i; j-gap>=0 && arr[j]<arr[j-gap]; j-=gap) {
int temp=arr[j];
arr[j]=arr[j-gap];
arr[j-gap]=temp;
}
}
}
3.直接选择排序
核心思路
直接选择排序:每次在无序区间中选择最小值与无序区间的第一个元素交换,直到整个数组有序。
排序步骤
- 定义下标 i 为当前无序区间的第一个元素,下标 min 为无序区间的最小值,下标 j 遍历无序区间。
- 有序区间:[0…i)
- 无序区间:[i…n)
- j 遍历无序数组,若 j 指向的元素小于min指向的元素,则min指向此元素。
- 遍历完之后,将min指向的元素与 i 指向的元素交换。

代码
public static void select(int[] arr){
//有序区间:[0,i)
//无序区间:[i,n)
int n=arr.length;
//当无序区间只剩下一个元素时,已经不用再排了
for (int i=0; i < n-1 ; i++) {
//min指向无序区间的最小值
int min=i;
for (int j = i+1 ; j < n ; j++) {
if(arr[j]<arr[min]){
min=j;
}
}
//此时min一定指向无序区间的最小值
int temp=arr[i];
arr[i]=arr[min];
arr[min]=temp;
}
}
缺点
无论数组是否接近有序,直接选择排序都会执行一遍内部的排序流程,对数据不敏感。
4.堆排序
🌙原地堆排序写在另一篇文章了~
⭐原地堆排序
5.冒泡排序
核心思路
重复扫描待排序序列,并比较每一对相邻的元素,当该对元素顺序不正确时进行交换。一直重复这个过程,直到没有任何两个相邻元素可以交换,就表明完成了排序。
排序步骤
- 比较相邻两个数据如果。第一个比第二个大,就交换两个数
- 对每一个相邻的数做同样1的工作,这样从开始一队到结尾一队在最后的数就是最大的数。
- 针对所有元素上面的操作,除了最后一个。
- 重复1~3步骤,直到顺序完成。

代码
public static void bubbleSort(int[]arr){
//外层循环表示要进行元素操作的趟数
for (int i = 0; i < arr.length-1; i++) {
boolean isSwaped=false;
for (int j = 0; j < arr.length-i-1; j++) {
if(arr[j]>arr[j+1]){
isSwaped=true;
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
if(!isSwaped){
break;
}
}
}
6.快速排序
🌙快速排序写在另一篇文章了~
⭐快速排序详解
7.归并排序
核心思路
1.归: 先不断的将原数组一分为二,直到拆分后的子数组只剩下一个元素。(当数组只有一个元素时,天然有序)
2.并: 不断的将两个连续的有序子数组合并为一个大的数组,直到整个数组合并完成。

排序步骤
并的核心步骤:给定一个临时数组 aux 存储即将归并的子数组的值。
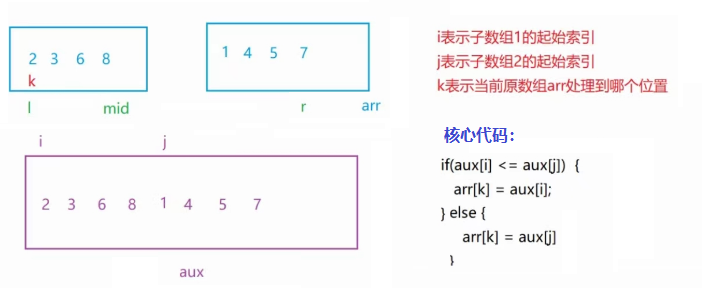
代码
public static void mergeSort(int[]arr){
mergeSortInternal(arr,0,arr.length-1);
}
private static void mergeSortInternal(int[] arr, int l, int r) {
if(l>=r){
return;
}
int mid=l+((r-l)>>2);
//先将原数组一分为二,在子数组上进行归并排序
mergeSortInternal(arr,l,mid);
mergeSortInternal(arr,mid+1,r);
//此时两个子数组已经有序,将两个子数组合并为原数组
merge(arr,l,mid,r);
}
private static void merge(int[] arr, int l, int mid, int r) {
//创建一个临时数组
int[] aux=new int[r-l+1];
//拷贝子数组的数据到临时数组上
System.arraycopy(arr,l,aux,0,r-l+1);
//两个子数组的开始索引
int i=l;
int j=mid+1;
//k表示当前原数组合并到哪个位置
for (int k = l; k <= r; k++) {
if(i>mid){
//此时子数组1全部拷贝完毕,将子数组2的内容全部写回
arr[k] = aux[j-l];
j++;
}else if(j>r){
//此时子数组2全部拷贝完毕,将子数组1的内容全部写回
arr[k] = aux[i-l];
i++;
}else if(aux[i-l]<=aux[j-l]){
arr[k]=aux[i-l];
i++;
}else{
arr[k]=aux[j-l];
j++;
}
}
}
补充:希尔排序的图片参考了这篇博文:希尔排序