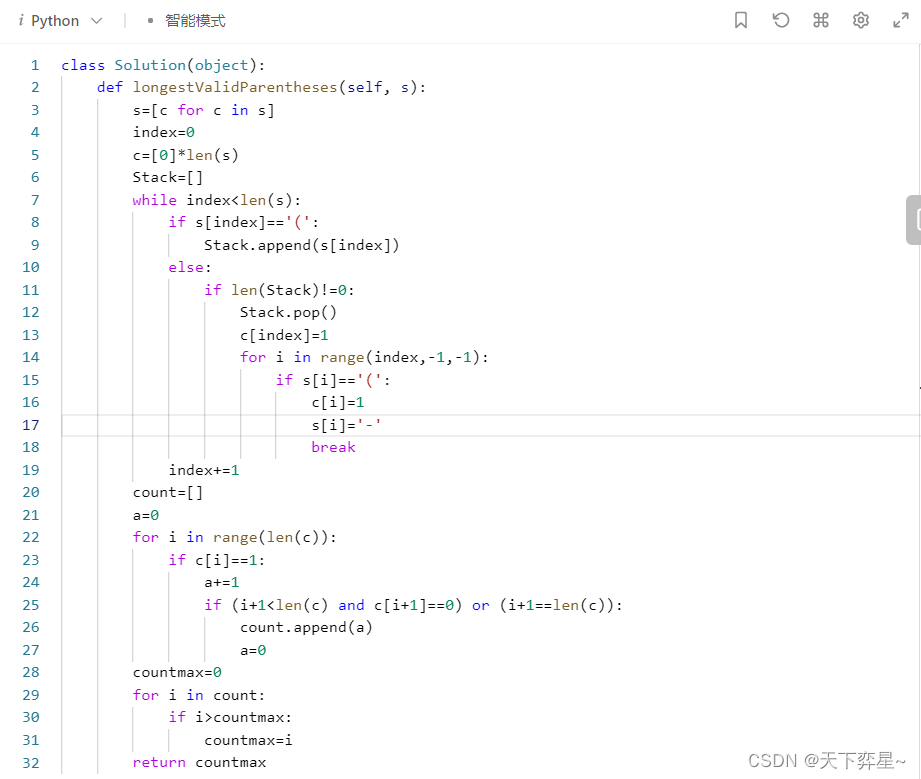
题目大意： 给出一个n个点的树，所有点权a[i]构成一个n的排列，点权可以任意分配给点，问最多有多少对u,v满足a[u]<lca(a[u],a[v])<a[v]

2<=n<=5000

思路：首先，如果两个点的lca是他俩其中之一，那么肯定不符合条件，所以符合条件的点对一定分别在一个点的两条子链上，我们先考察最小的子树，也就是像下图这样根的所有子链都没有分支：

可以发现，我们要让满足要求的数对最多，所以要么一条链上的点全部大于lca或全部小于lca，这样的话例如一条链长x全小于lca，一条长y，全大于lca，他们的贡献就是x*y如果有一对反过来，就会变成(x-1)*(y-1)+1*1，肯定更小。

那么问题就转变成了有x个数（x为子链数），怎样将这x个数分成两部分，使得一部分的和*另一部分的和最大，因为和最大是5000,所以我们可以用类似01背包的方法，求出所有能凑出来的和，即将所有所有链长存入数组q中，数组occ记录哪些和出现过，对于q[i]，我们从5000到0枚举j，如果occ[j]=1，那么occ[j+q[i]]也为1，之所以要倒推就是因为一个数只能取一次，不能重复取，然后从1到sum(子节点总数)遍历i，如果occ[i]=1，就维护i*(sum-i)的最大值

这样我们就求出了对于上面这样的最小子树的答案数量，之后对于每个有多个子节点的点，都按此法将他们的子树长度分成两份，求和求乘积最大即可

 

//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
const int N = 5e3 + 5;
typedef long long ll;
const int INF = 0x7fffffff;
int head[N], tot = 0;
struct Edge
{
	int v, next;
}e[N];
void addedge(int u, int v)
{
	e[++tot].v = v;
	e[tot].next = head[u];
	head[u] = tot;
}
int n;
ll cnt[N];
void init()
{//初始化
	for (int i = 1; i <= n; i++)
	{
		cnt[i] = 0;
		head[i] = -1;
	}
	tot = 0;
}
ll ans = 0;
bool occ[N];
void dfs(int u)
{
	vector<ll>q;
	ll sum = 0;
	for (int i = head[u]; ~i; i = e[i].next)
	{
		int v = e[i].v;
		dfs(v);
		q.push_back(cnt[v]);//记录每棵子树的大小
		cnt[u] += cnt[v];//求子树大小
	}
	cnt[u] += 1;
	if (q.size()<=1)
		return;//子树数量<2肯定没贡献
	ll ma = 0;
	for (int i = 1; i <= n; i++)
	{
		occ[i] = 0;
	}
	occ[0] = 1;
	for (int i = 0; i < q.size(); i++)
	{//枚举每一棵子树
		sum += q[i];
		for (int j = n; j >= 0;j--)
		{//总合不超过n
			if (occ[j])
			{//j取过，q[i]就能取
				occ[j + q[i]] = 1;
			}
		}
	}
	for (int i = 1; i < sum; i++)
	{
		if (occ[i])
		{//枚举所有出现过的和，维护最大值
			ma = max(ma, i * (sum - i));
		}
	}
	ans += ma;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> n;
	init();
	for (int i = 1; i < n; i++)
	{
		int u;
		cin >> u;
		addedge(u, i + 1);
	}
	dfs(1);
	cout << ans << endl;
	return 0;
}