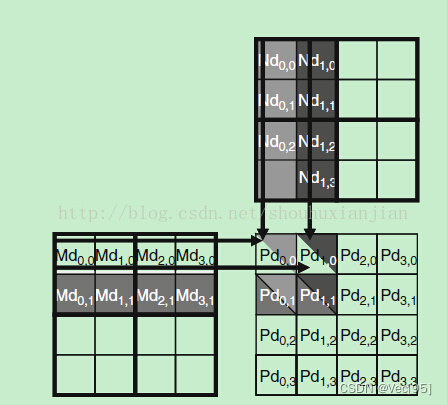
kenel的block中的每个线程用于计算共享内存中矩阵Pd中的一个元素Pd_(i，j)，每个线程都读取Md的一行和Nd的一列。Pd_(0，0)和Pd_(1,0)两个结果是由两个线程完成的。这里一开始只有Pd被加载进共享内存，Md和Nd还在全局内存中：

                                      

上图是一个4×4的矩阵与4×4的矩阵相乘的过程，其中将使用2×2的块block，即每个block中有四个线程，也就是共享内存中的Pd矩阵分成四个块，每个大小2x2来执行，使得block中每个线程计算Pd中一个元素。

上图显示的是（0，0）块的执行结果，按照矩阵乘法的过程可以看出，得到Pd_(0，0)和Pd_(1,0)两个结果是由两个线程完成的，但是它两都需要访问Md矩阵的第一行的四个值，这就说明Md矩阵的第一行需要被访问两次（这里的前提是分块的第一个块中，当然不同块之间还是会有重复访问的问题）；同样的也会访问Nd矩阵的每一行两次（每一列两次？），如果说能够采用某种方法使得线程（0，0）和线程（1，0）之间能够合作，那么Md中的元素只要从全局存储器中加载一次就行了，这样对于全局存储器的访问就减少了一半。这里可以发现矩阵乘法这个例子中全局存储器流量潜在的减少量与使用的块的维度成正比，对于N×N的块来说，全局存储器流量就可以减少N倍，也就是流量只有原来的1/N了。
 

这就是使用线程合作的方式将Md和Nd中的元素加载到共享存储器中，但是共享存储器容量相当小，所以还是得注意，不过可以将矩阵Md和Nd中的元素划分成更小的块，而且块的大小是可以选择的，从而放在共享存储器中。

最简单的就是将共享内存中Md和Nd中分成的块的维度等于kenel的块block的维度：把Md和Nd划分成2x2的块放进共享内存：

通过将Md和Nd两个矩阵也分成2×2的块，然后单独的将不同的块加载到共享存储器中，所以得到的Pd值也被分成几个不同的阶段：

第一阶段，

把Md(0,0)，Md(1,0)，Md(0,1)，Md(1,1)，送入Mds(0,0)，Mds(1,0)，Mds(0,1)，Mds(1,1).（行主序）。

把Nd(0,0)，Nd(1,0)，Nd(0,1)，Nd(1,1)，送入Nds(0,0)，Nds(1,0)，Nds(0,1)，Nds(1,1).（列主序）。

然后用于计算Pd(0,0),Pd(0,1),Pd(1,0),Pd(1,1)。注意计算过程中的行列主序。

第二阶段，

把Md(2,0)，Md(3,0)，Md(2,1)，Md(3,1)，送入Mds(0,0)，Mds(1,0)，Mds(0,1)，Mds(1,1).(行主序）。

把Nd(0,2)，Nd(1,2)，Nd(0,3)，Nd(1,3)，送入Nds(0,0)，Nds(1,0)，Nds(0,1)，Nds(1,1).（列主序）。

然后用于计算Pd(0,0),Pd(0,1),Pd(1,0),Pd(1,1)。注意计算过程中的行列主序。

在每个阶段中，一个块中所有的线程相互合作将Md和Nd中的块加载到共享存储器中：

上图就是具体的执行过程，时间从左往右，其中Mds和Nds表示在共享存储器中对应的位置，线程T_(0，0)负责在第一阶段中将Md_(0,0)和Nd_(0,0)加载到对应的共享寄存器中，以此类推，在阶段一中当加载了Md和Nd矩阵的对应的第（0，0）块的时候，计算一半的值；然后进行第二阶段加载Md和Nd矩阵的（0，1）的块然后接着计算后一半的值。

一般来说，如果一个输入矩阵的维度是N而且块大小为TILE_WIDTH（就是想要将这个矩阵分成的小块的维度，比如上面4×4的矩阵分成的小块的维度是2），那么点积运算分成N/TILE_WIDTH个阶段。这种将每个阶段中使用输入矩阵元素的一个很小的子集，这种集中访问的行为称为局部性。所以如果一个算法能够具有这种局部性，那么无论是在多核CPU还是GPU中，都可以提高性能。

下面就是实现上面步骤的例子代码：

注意这里要用kenel的线程号bx,tx,by,ty乘以共享内存中矩阵的边长TILE_WIDTH来得到矩阵元素的行、列序号。将kenel，block中的线程与共享内存中需要用线程处理的元素连接起来。

代码解释：第一行和第二行进行声明Mds和Nds为共享存储器变量；第三行和第四行将线程索引和块索引放入自动变量中，所以可以利用寄存器来快速的访问这些变量（在函数中自动的标量变量是会放入寄存器中的，作用域是单个线程，也就是每个线程会有tx,ty,bx,by的私有版本）；第五行和第六行创建对应的Pd矩阵的行索引和列索引：

上图就是用来解释第五行和第六行的代码的，如何来进行索引Pd矩阵；第八行中m指明点积执行过程中现在执行第几个阶段，每个阶段用到Md中的一个块元素和Nd中的一个块元素，表示已经执行完Md和Nd中m×TILE_WINDTH对元素了；

第九行和第十行就是通过一个块中的线程协作的方式将Md和Nd中一个块内的数据加载到共享存储器中，因为这里还是将2维矩阵以1维向量存储的方式，所以先跳过前面的Row*Width个，从第（Row+1）行开始计算；第十一行使用栅栏同步函数_syncthreads（），确保同一个块中所有的线程都加载好了Mds和Nds；第十二行和第十三行用来计算第m个阶段上的点积部分；第十四行再次调用栅栏同步函数，用于进入下一次的循环中加载Md和Nd的下一个块，保证当前块中所有的线程都已经使用完Mds和Nds的数据。

        虽然采用寄存器，共享存储器和常数存储器可以有效的减少对全局存储器的访问，但是它们自身也是有容量限制的，如果说每个线程要求的存储单元越多，那么每个SM中可以同时驻留的线程就越少，导致在整个存储器中驻留的线程数也越少。假设（G80中）一个SM中寄存器大小为8KB，而且最多能够容纳768个线程，那么每个线程可使用的寄存器个数为8KB/768 = 10.如果每个线程使用11个寄存器，那么线程数目势必要减少，而且是以块的形式来减少的，如果当前块中执行的有256个线程，那么算下来每个SM中可同时驻留的线程数就减少256个，只有512个，使得大大减少线程调度是可用的warp的数量（个人：这里的SM中可以最大驻留768个线程，而一个SM中的寄存器是放在一起的不是单独线程分开的，然后你在kernel函数中指定了块的维度，也就是一个块中有256个线程，那么方便调度就从768减去256，如果寄存器还是不够用那么接着在减少256个线程，这样就使得在kernel中分配的块能够放在一个SM中运行）；同样的共享存储器也是个问题，假设（G80）每个SM中共享存储器的大小为16KB，而这总的16Kb是以块划分而不是像上面的8KB的寄存器一样以线程划分，如果每个块使用5KB的共享存储器，那么每个SM最多只能分配3个块。在上面的代码例子中，假设对于16×16的块来说，每个块使用16×16×4 = 1KB的存储空间来存放Mds，同理需要1KB空间存放Nds，每个块需要使用2KB的共享存储空间，但是因为线程的硬件限制，每个SM最多容纳768个线程，使得最多只有3个块，那么只能使用共享存储器的6KB的空间，就浪费了10KB的空间了，不过硬件的限制是因显卡的更新换代而不同的，比如GT200中每个SM最大支持1024个线程。