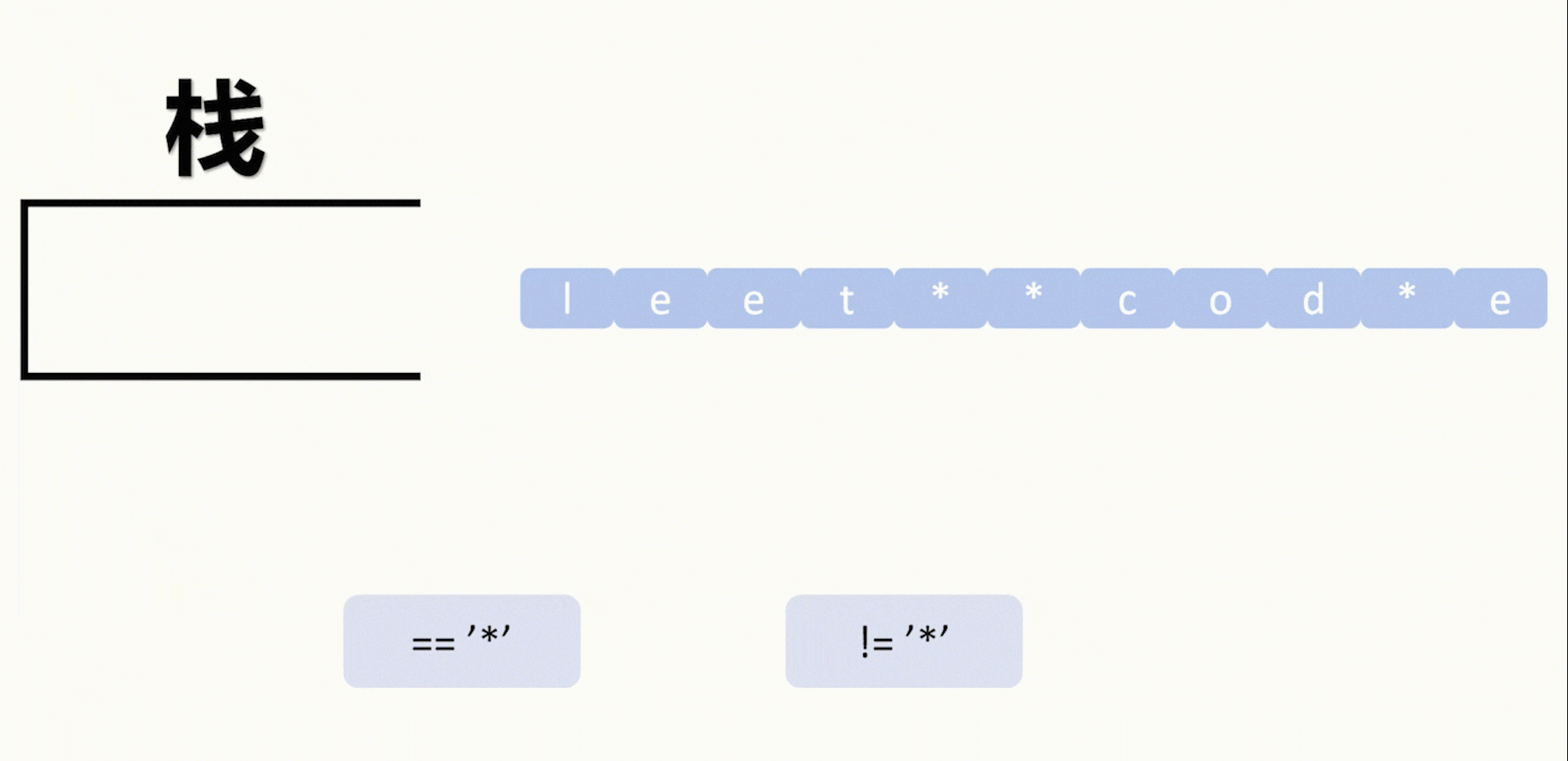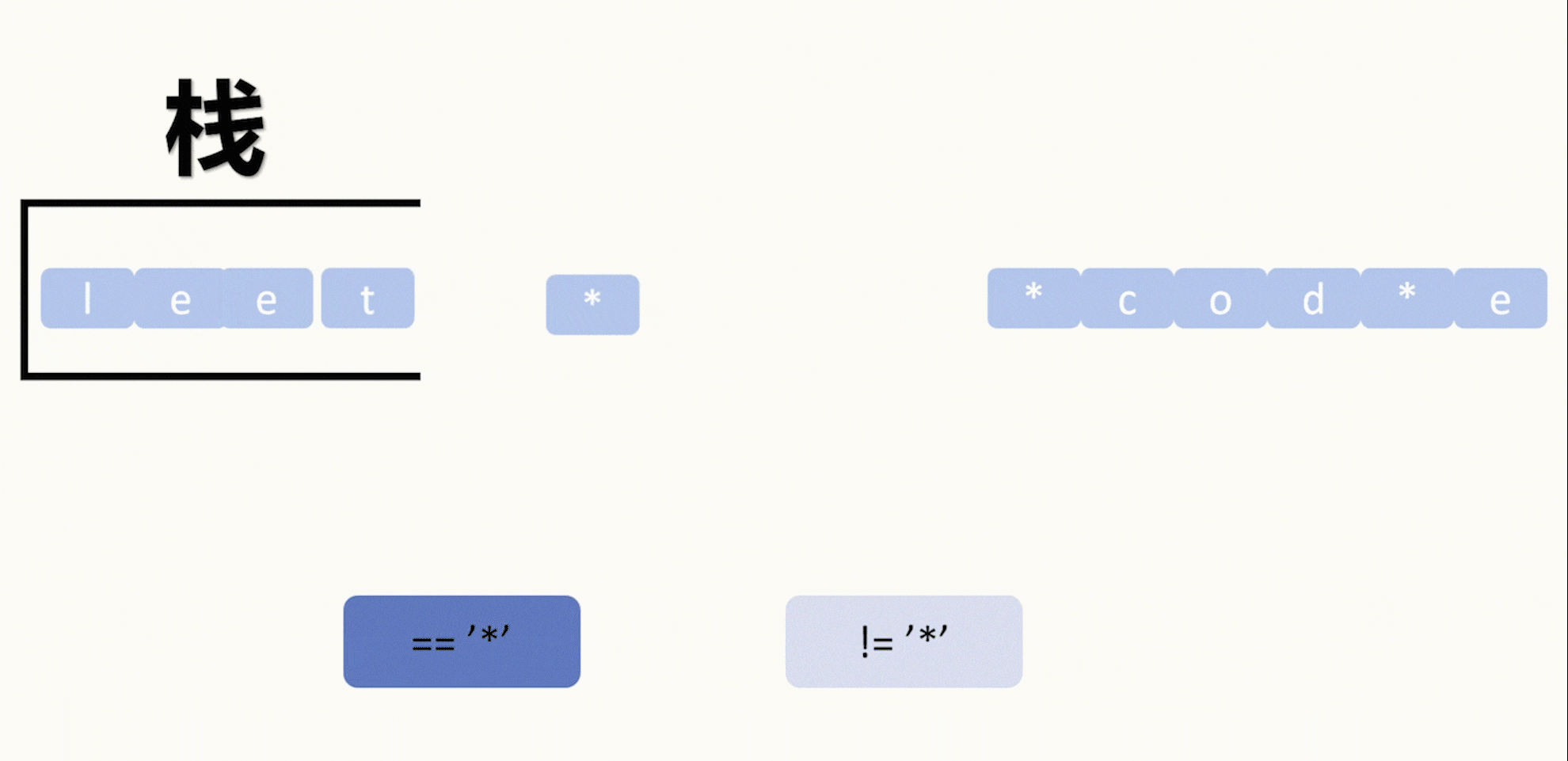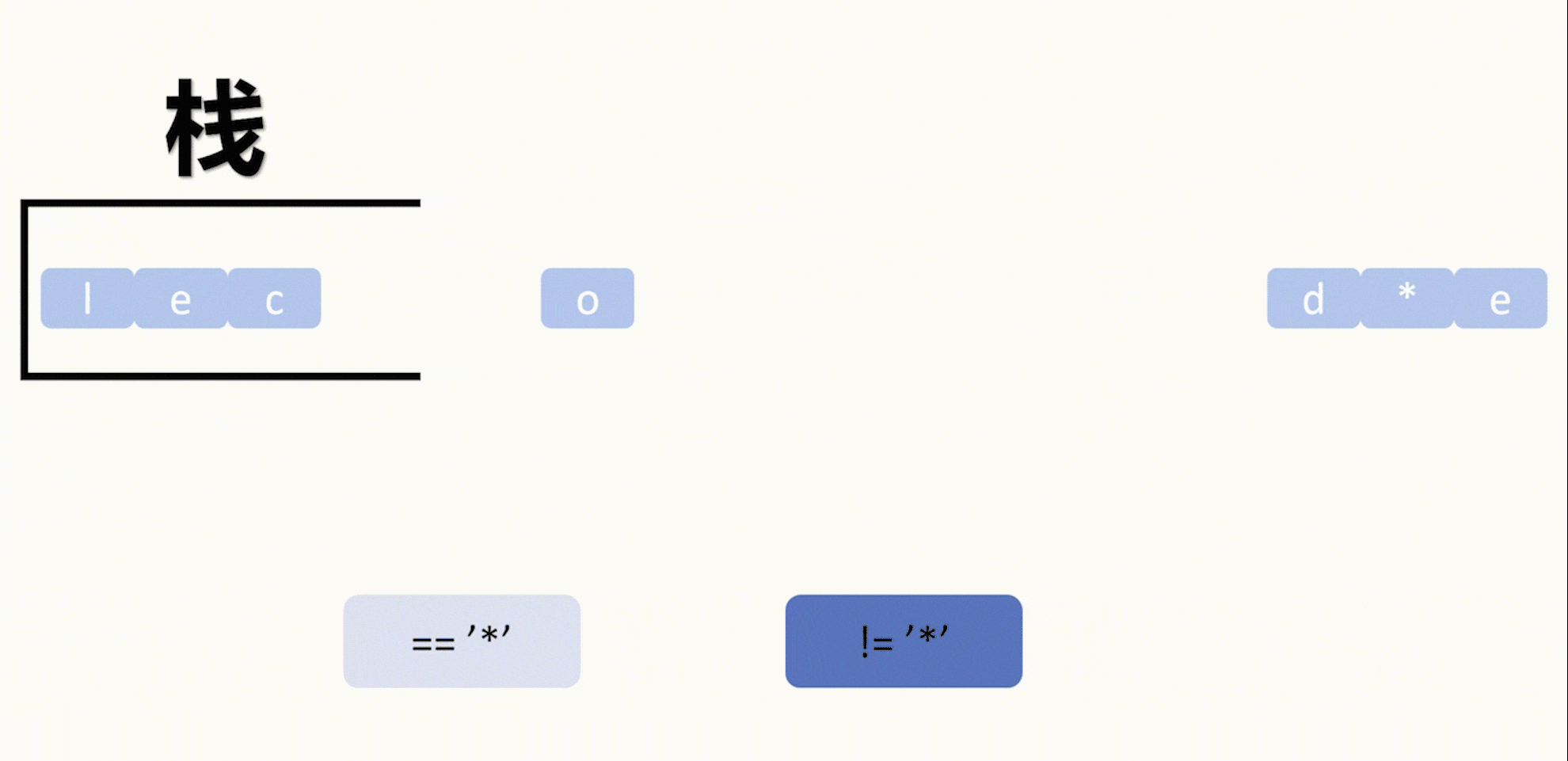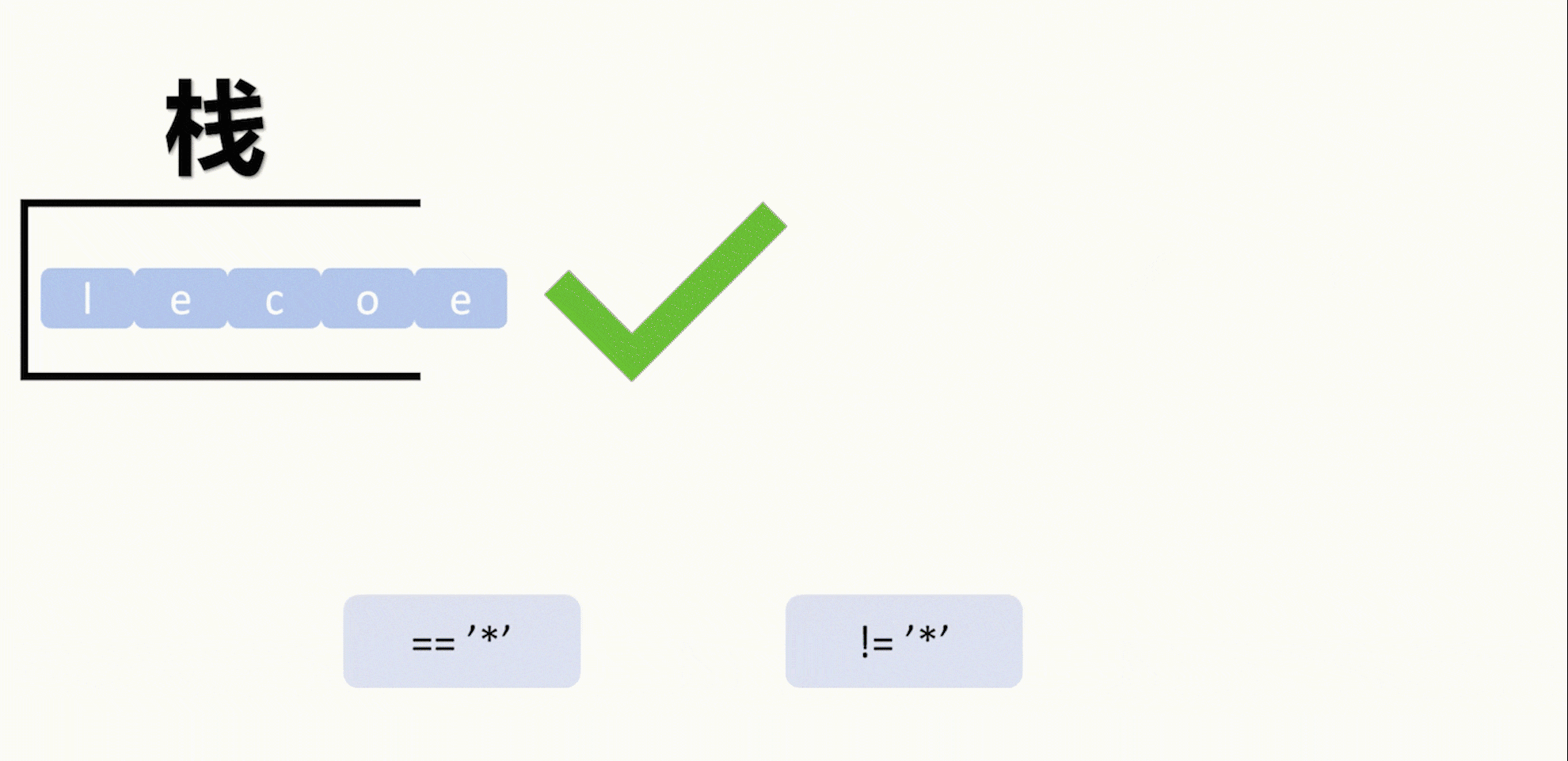
马尔可夫链的重要性质以及两个例题如下：

注意：

1. 例5中有几个地方需要注意：
   （1）为什么$P_{11}=P_{22}=pq+(1-p)(1-q)，而P_{33}=pq+(1-p)$?这里要看到上述题目中的限制条件，“一个需要服务的顾客到达系统时发现系统内有3个顾客则该顾客即离去”。因此，当顾客数是3时，不会发生q或者1-q。
   （2）为什么$P_{ij}=0(|i-j|\ge 2)$?请看下面第3点的论述。
   （3）为什么$\Delta t\to 0$的真是含义是什么？当$\Delta t\to 0$时，在此时间间隔内，事件发生两次的概率极限为0。
2. 思考一下，例6中哪里体现了马尔可夫过程的齐次性呢？所有的条件转移概率都用$P_{ij}(1)$来代替，既体现了马尔可夫链的齐次性原理。