整数规划——第七章分支定界算法

目前大部分整数规划商业软件如CPLEX，Gurobi和BARON等都是基于分枝定界算法框架的。

7.1 最优性条件和界

考虑下列一般线性整数规划问题：
$\text{(IP)}\quad\begin{aligned} &\min c^Tx,\\ &s.t.\ Ax\le b,\\ &\qquad x\in \Z_+^n \end{aligned}\tag{7.1}$
其中 $Z_+^n$ 是 $R^n$ 中的非负整数集合，给定（IP）的可行点 $x^*$ ，如何验证 $x^*$ 是（IP）的最优解？

设 $f^*$ 是（IP）的最优值，假设可以产生 $f^*$ 的下界序列满足：
$\underline{f}_1\le \underline{f}_2\le \cdots\underline{f}_k\le \cdots\le f^*,$
同时可以产生 $f^*$ 的上界序列满足
$\overline{f}_1\ge \overline{f}_2\ge \cdots \ge\overline{f}_k\ge \cdots \ge f^*$
若 $\overline f_k-\underline f_k\le \varepsilon$ 对一个很小的 $\varepsilon \ge 0 $ 成立，则显然有
$f^*-\varepsilon \le \underline{f}_k\le f^*$
问题（IP）的任何可行解 $x^k$ 都对应 $f^*$ 的一个上界 $f(x^k)=\overline{f}_k$ ，若 $\overline f_k-\underline f_k\le \varepsilon >0$ ，则 $x^k$ 是一个 $\varepsilon$ 近似最优解，显然有如下定理：

定理7.1 设 $\{\overline f_k\}$ 和 $\{\underline f_k\}$ 是 $f^*$ 的上界序列和下界序列，若 $\overline f_k-\underline f_k=0$ 且 $x^k$ 是（IP）的可行解， $f(x^k)=\overline f_k$ ，则 $x^k$ 是（IP）的最优解。

常用的求线性整数规划问题下界的方法有两种：线性规划松弛和对偶松弛。

定义7.1 线性规划
$\text{(LP)}\quad\begin{aligned} &\min c^Tx,\\ &s.t.\ Ax\le b,\\ &\qquad x\in \R_+^n \end{aligned}$
成为整数规划（7.1）的线性规划松弛，也称为（LP）的连续松弛。

显然，（LP）的最优值总是（IP）的最优值的一个下界，易证下列性质：

定理7.2

若（LP）不可行，则（IP）也不可行；
设 $x^*$ 是（LP）的最优解且 $x^*∈\Z^n$ ,则 $x^*$ 也是（IP）的最优解.

拉格朗日对偶松弛是另一种很有用的定界方法。考虑下面的整数规划问题：
$\text{(IP)}\quad\begin{aligned} &\min c^Tx,\\ &s.t.\ Ax\le b,\\ &\qquad x\in X \end{aligned}\tag{7.2}$
此处 $X$ 是一个整数集合，如 $X=\{0,1\}^n，X=\{x\in \Z^n\ |\ l\le x\le u\}$ 。设 $\lambda \in \R_+^m$ ，考虑朗格朗日松弛问题：
$d(\lambda)=\underset{x\in X}{\min}c^T x+\lambda^T(Ax-b)$
则对任意（7.2）的可行解 $x$ 和 $\lambda \in \R_+^m$ ，有 $d(\lambda) \le c^Tx$ ，故 $d(\lambda)$ 是（IP）的一个下界，而最优的下界可以由下列对偶问题得到：
$(D)\qquad \underset{\lambda\in \R_+^m}{\max}\ d(\lambda)$
在许多情况下计算拉格朗日松弛界 $d(\lambda)$ 往往很容易，如当 $X=\{0,1\}^n$ 时，
$d(\lambda) = -\lambda^Tb+\sum_{i=1}^n\min\{0,c^i+\lambda^Ta_i\}$
其中 $a_i$ 是 $A$ 的第 $i$ 列。

7.2 分支定界方法：0-1背包问题

考虑以下0-1背包问题：
$\text{(0-1 KP)}\qquad\begin{aligned} &\max c^Tx, \\ & \text{s.t.}\ a^Tx\le b\\ &\quad\ \ \ x\in \{0,1\}^n \end{aligned}$
这里 $c_i>0,a_i>0,i=1,...,n$ ，问题（0-1KP）的线性规划松弛为：
$\text{(CKP)}\qquad\begin{aligned} &\max c^Tx, \\ & \text{s.t.}\ a^Tx\le b\\ &\quad\ \ \ x\in [0,1]^n \end{aligned}$
使用贪心法来求解，将 $\{\cfrac{c_i}{a_i}\}$ 按降序排列，设：
$\frac{c_1}{a_1} \ge \frac{c_2}{a_2}\ge \cdots\ge \frac{c_n}{a_n}\tag{7.3}$
设 $s$ 是使下式成立的最大指标 $k$ ：
$\sum_{j=1}^ka_j\le b\tag{7.4}$
定理7.3 线性规划问题（CKP）的最优解为：
$\begin{aligned} &x_j=1,\quad j=1,...,s\\ &x_j=0,\quad j=s+2,...,n\\ &x_{s+1}=(b-\sum_{j=1} ^sa_j)/a_{s+1}\\ \end{aligned}$
设 $f^*$ 是（0-1KP）的最优值，若 $c_j$ 都是整数，则 $f^*$ 也是整数，故 $f^*$ 的一个上界为
$z=\sum_{j=1} ^sc_j+\left\lfloor(b-\sum_{j=1}^s a_j)c_{s+1}/a_{s+1} \right\rfloor$
例7.1 考虑下列0-1背包问题：
$\begin{aligned} &\max 8x_1+11x_2+6x_3+4x_4\\ &\text{s.t.}\ 5x_1+7x_2+5x_3+3x_4\le 14\\ &\qquad x\in \{0,1\}^4 \end{aligned}$
应用定理7.3，该问题的线性规划松弛的最优解为 $x=(1,1,\cfrac{1}{2},0)^T$ ，对应的上界为 22。选择变量 $x_3$ 进行分枝，固定 $x_3=0$ 和 $x_3=1$ ，得到两个子问题：
$(P_1)\quad\begin{aligned} &\max 8x_1+11x_2+4x_4\\ &\text{s.t.}\ 5x_1+7x_2+3x_4\le 14\\ &\qquad x_1,x_2,x_3\in \{0,1\} \end{aligned}$

$(P_2)\quad\begin{aligned} &\max 6+ 8x_1+11x_2+4x_4\\ &\text{s.t.}\ 5x_1+7x_2+3x_4\le 10\\ &\qquad x_1,x_2,x_3\in \{0,1\} \end{aligned}$

子问题 $P_1)$ 的线性规划松弛的最优解为 $(1,1,\cfrac{2}{3})^T$ ，对应的上界为 $z = 21.67$ 。子问题 $P_2)$ 的线性规划松驰的最优解为 $(1,\cfrac{5}{7},0)^T$ ，对应的上界为 $z = 21.86$ 。分枝过程见图7.1.

选择子问题 $P_2)$ ，选择变量 $x_2$ 进行分枝，固定 $x_2=0$ 和 $x_2=1$ ，得到2个子问题：
$(P_3)\quad\begin{aligned} &\max 6+8x_1+4x_4\\ &\text{s.t.}\ 5x_1+3x_4\le 10\\ &\qquad x_1,x_4\in \{0,1\} \end{aligned}$

$(P_4)\quad\begin{aligned} &\max 17+8x_1+4x_4\\ &\text{s.t.}\ 5x_1+3x_4\le 3\\ &\qquad x_1,x_4\in \{0,1\} \end{aligned}$

子问题 $P_3)$ 的最优解为 $1,1)^T$ ，对应原问题的一个可行解 $x=(1,0,1,1)^T$ ，目标函数值为 $z = 18$ 。子问题 $P_4)$ 的线性规划松弛的最优解为 $(1,\cfrac{3}{5})^T$ ，对应的上界为 $z = 21.80$ ，分支过程见图7.2。

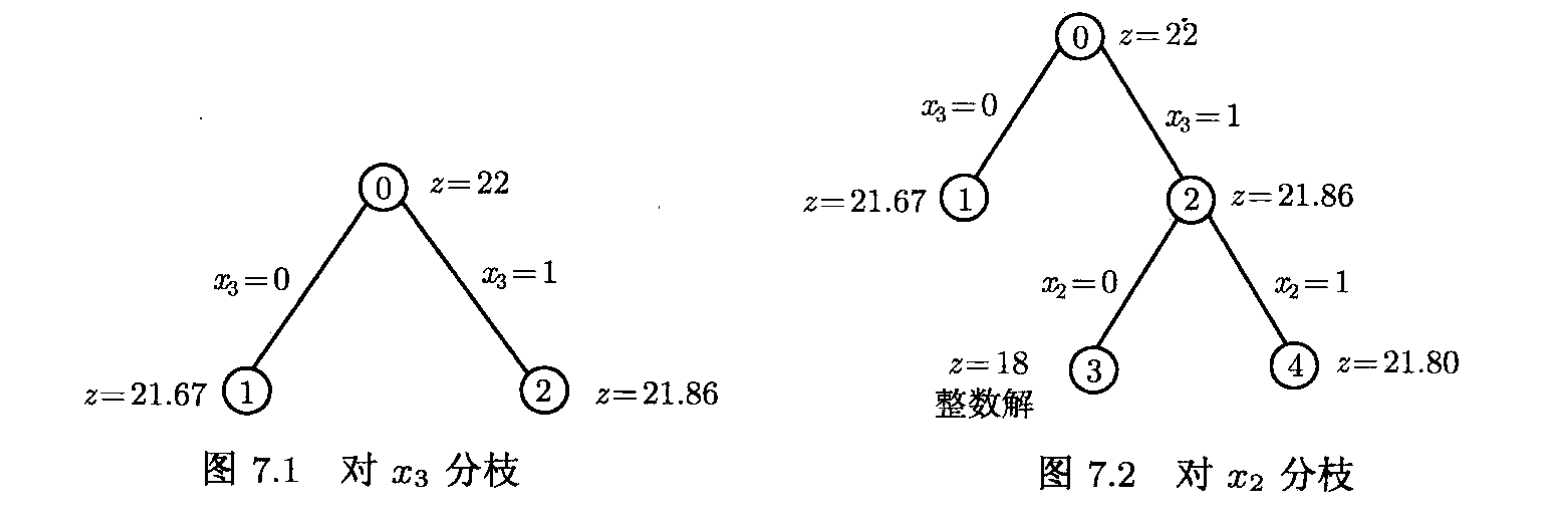
在这里插入图片描述

选择子问题 $P_4)$ 并对 $x_1$ 进行分枝，固定 $x_1=0$ 和 $x_1=1$ 得到2个子问题：
$(P_5)\quad\begin{aligned} &\max 17+4x_4\\ &\text{s.t.}\ 3x_4\le 3\\ &\qquad x_4\in \{0,1\} \end{aligned}$

$(P_6)\quad\begin{aligned} &\max 25+4x_4\\ &\text{s.t.}\ 3x_4\le -2\\ &\qquad x_4\in \{0,1\} \end{aligned}$

易见，子问题 $P_5)$ 的最优解为 $x_4=1$ ，对应原问题的一个可行解 $x=(1,1,0,1)^T$ ，其目标函数值为 $z = 21$ 。而子问题 $P_6)$ 不可行。分枝过程见图7.3。因为节点1对应的
子问题 $P_1)$ 的上界为21.67且原问题的最优值为整数，故子问题 $P_1)$ 不可能产生
比 $x=(1,1,0,1)^T$ 更好的可行解。从而推断出所有 ${0,1\}^4$ 中没有比 $x=(1,1,0,1)^T$
更好的可行解，故 $x=(1,1,0,1)^T$ 是原问题的最优解。

由上述例子可以看出，分枝定界过程中产生的子问题之间的关系是一树状结构，以后称之为分枝定界树或搜索树。分枝定界求解0-1背包问题的基本思想可以总结如下：

算法7.1(0-1背包问题分枝定界算法)

初始步.求解原问题的线性规划松弛，若得到整数解则也是原问题的最优解，否则得到原问题的一个上界.

分枝：选择适当的变量 $x_i$ ，分别固定 $x_i=0$ 和 $x_i=1$ 得到2个子问题。
定界：选择一个子问题，求解该子问题的线性规划松弛。
剪枝：若发生下列情况之一，则可停止对该子问题进行分枝（剪枝）：
- 子问题的线性规划松弛的最优解是整数解；
- 子问题不可行；
- 子问题的上界等于或小于已知的可行解的目标函数值。

最优性.重复上述过程直到分枝定界树中没有需要考虑的节点（子问题），当前最好的可行解就是原问题的最优解。

7.3 分支定界方法：一般线性整数规划

本节讨论下列一般线性整数规划问题：
$\text{(IP)}\quad\begin{aligned} &\min c^Tx,\\ &s.t.\ Ax\le b,\\ &\qquad x\in \Z_+^n \end{aligned}$
记 $S=\{x\in \Z_+^m|Ax\le b\}$ 。求解0-1背包问题的算法7.1可以推广到一般整数规划问题，只要使用适当方法把子问题的可行域剖分为若干个小的子集，一般是把可行域分成2个部分，从而可以产生类似于0-1背包问题的分枝定界树。设子问题的线性规划松弛解为 $x^0=(x_1^0,...,x_n^0)^T$ ，其中至少有一个 $x_i^0$ 是分数。假设选取变量进行分枝，一种自然的剖分方法是分别设
$x_i\le \left\lfloor x_i^0 \right\rfloor ,x_i\ge \left\lfloor x_i^0 \right\rfloor+1$
$\left\lfloor \right\rfloor$ 表示取下整。则得到2个新的节点（子问题），如图7.4所示。显然，上述对整数规划可行域的剖分并不会丢失任何整数可行点。

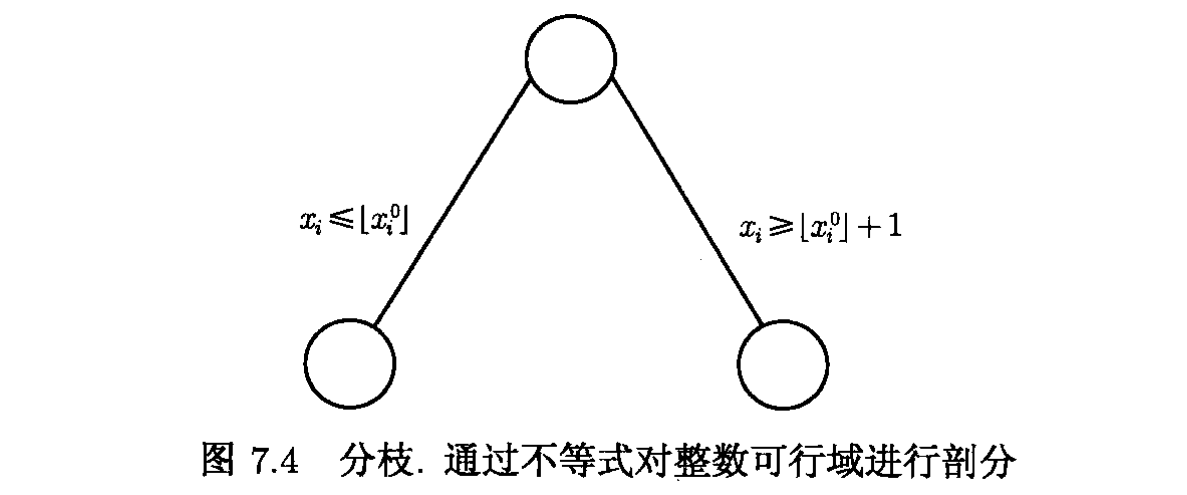
在这里插入图片描述

选择分枝变量的基本策略是使分枝后的2个子问题的线性规划松弛界与当前问题的界之间的差别尽可能大，这样就有可能尽早进行剪枝。常用的方法是选取
$i=\arg \max\{\min(x_j^0-\lfloor x_j^0 \rfloor ,\lceil x_j^0 \rceil -x_j^0)\ |\ x_j^0为分数\}$
在分枝定界过程中，在剪枝后如何从搜索树中剩下的节点（子问题）中选择一个节点继续进行分枝也将影响整个分枝定界的收敛速度。常用的策略有

下界优先：总是选择下界最小的节点进行分枝，这里的下界可以是线性规划松弛界，或者是指该节点继承其父节点的下界
深度优先：把分枝定界树的层数（已分枝变量的个数）定义为节点的深度，深度优先策略是选择具有最大深度的节点进行分枝，从而能比较快地找到可行解。

例7.2 考虑下列线性整数规划问题：
在这里插入图片描述

该问题的线性规划松弛的最优单纯形表见表7.1，故线性规划松弛的最优解为 $x=\left(\cfrac{20}{7},3\right)^T$ ，问题的下界为 $z=-\cfrac{59}{7}$ 。选择 $x_1$ 进行分枝，分别加入约束 $x_1\le2$ 和 $x_1\ge 3$ 得到两个子问题，如图7.5。选择节点1，其对应的线性规划是节点0的线性规划加上约束 $x_1\le 2$ ，其可以表示为 $x_1+s=2,s\ge0$ ，在表7.1中， $x_1$ 是基变量，可以用非基变量 $x_3$ 和 $x_4$ 表示，所以约束 $x_1\le 2$ 可以表示为：
$-\frac{1}{7}x_3-\frac{2}{7}x_4+s=-\frac{6}{7}$
在这里插入图片描述

将上述约束加入表7.1，可得单纯形表7.2。易见，以 $x_1,x_2,x_5,s)$ 为基变量的解对偶可行。经过 2 次对偶单纯形迭代，可得到最优单纯形表7.3。故节点1对应的线性规划最优解为 $x=\left(2,\cfrac{1}{2}\right)$ ，最优值为 $z=-\cfrac{15}{2}$ 。选择分数变量 $x_2$ 进行分枝，加入约束 $x_2≤0$ 和 $x_2≥1$ 得到2个子问题，见图7.6。应用深度优先选择节点3，其对应的线性规划的最优解为 $x=(\cfrac{3}{2},0)^T$ ，最优值为 $z = - 6$ ，继续选择节点4其对应的线性规划具有整数最优解 $x=(2,1)^T$ ，最优值为 $- 7$ 。
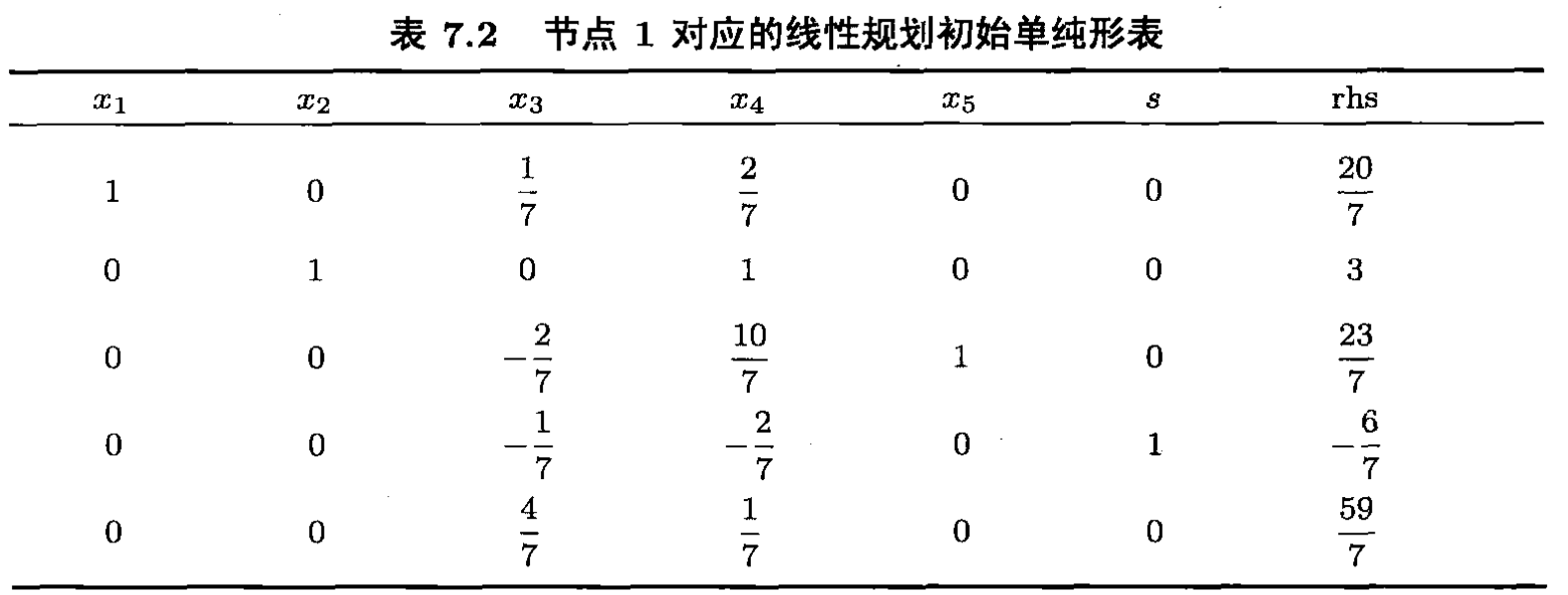
在这里插入图片描述

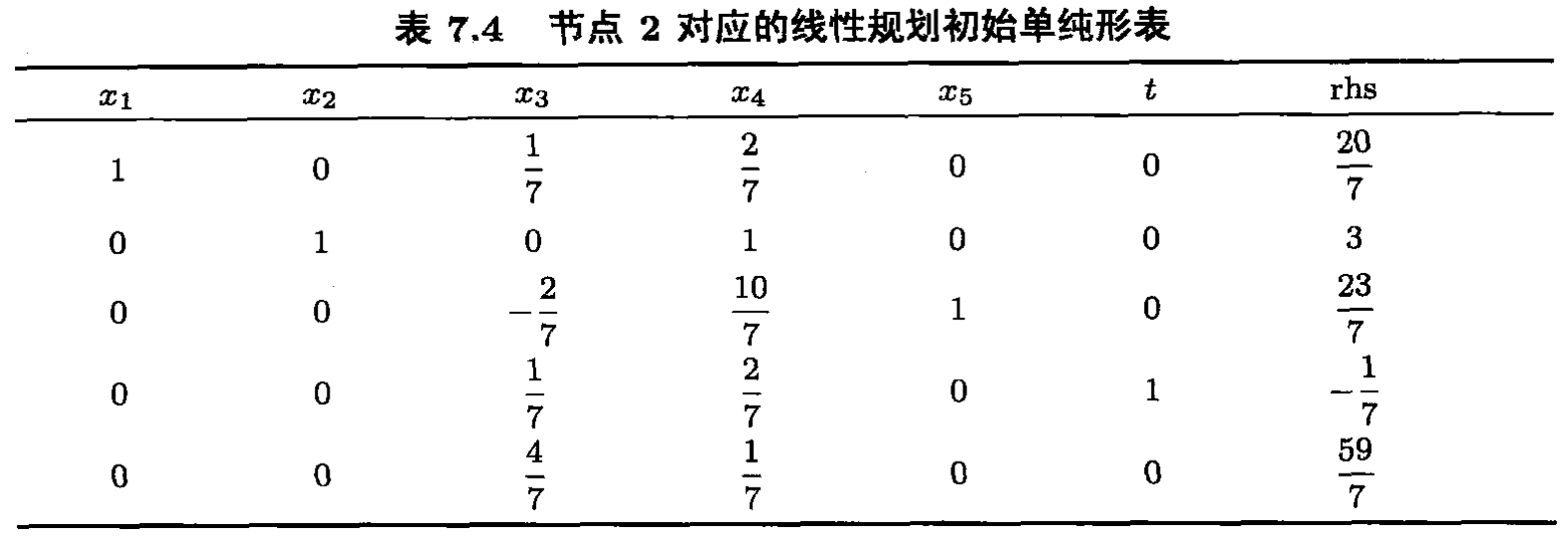
故节点3和4可以去除（剪枝），只剩下节点2需要考虑。把约束 $x_1≥3$ 写为 $x_1-t=3,t≥0$ 。类似地，可以把这个约束用表7.1中的非基变量 $x_3$ 和 $x_4$ 表示：
$\frac{1}{7}x_3+\frac{2}{7}x_4+t=-\frac{1}{7}$
把该约束加入单纯形表7.1得表7.4。容易看出，该线性规划不可行.故分枝定界树里已经没有节点需要考虑，当前最好的可行解 $x=(2,1)^T$ 就是原问题的最优解，见图7.7.
在这里插入图片描述

7.4 一般分支定界方法

考虑如下非线性整数规划问题：
$\text{(P)}\qquad\begin{aligned} &\min f(x),\\ & \text{s.t.} \ g_i(x)\le b_i,\quad i=1,...,m,\\ & \qquad h_k(x)=c_k ,\quad k,...,l,\\ &\qquad x\in X \end{aligned}$
其中 $f$ ， $g_i$ 和 $h_k$ 是 $R^n$ 中的实值函数， $X\in \Z^n$ 是一个整数集合。

为了应用分枝定界的基本框架，需要

对§的子问题定界的方法，如凸整数规划问题的连续松弛、线性下逼近方法可分离整数规划的拉格朗日松弛和二次0-1规划的半定规划(SDP)松弛；
求可行解的启发式方法，如贪婪法和根据问题的特殊结构设计的求可行解程序。

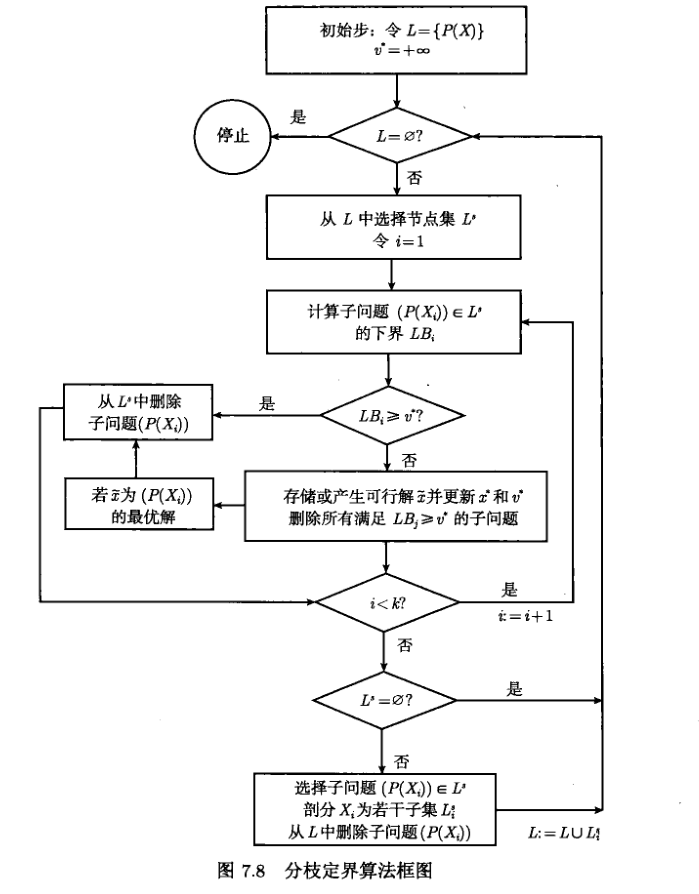
以下记 $P(X_i))$ 为§的一个子问题，其中 $X_i$ 是 $X$ 剖分后的子集，用 $L$ 记分枝定界树中存储的节点（子问题）集合。一般分枝定界的基本框架可以描述如下：

步0（初始步）：令 $L={P(X)}$ ，利用启发式算法求得问题的一个初始可行点 $x^*,v^*=f(x^*)$ 。若无初始可行解则令 $v^*=+∞$ .
步1（选择节点）：若 $L=\empty$ ，停止， $x^*$ 是原问题的最优解。否则，从L中选择一个或多个节点，记为 $L^s=\{P(X_1),\cdots，P(X_k)\}$ 。令 $i = 1$ 。
步2（定界）：计算子问题 $P(X_i))$ 的下界 $LB_i$ 。如果 $P(X_i))$ 不可行，则记 $LB_i=+∞$ 。若 $LB_i\ge v^*$ ，转步5。若 $P(X_i))$ 的松弛问题的最优解 $\tilde{x}$ 是整数解，若 $\tilde{x}$ 是比当前最好的可行解 $x^*$ 更好的解，更新 $x^*$ ，转步5。否则转步3。
步3（可行解）：利用启发式算法寻找可行解，若有则更新当前最好的可行解 $x^*$
和上界 $v^*$ 。若 $i < k$ ，令 $i := i + 1$ ，回到步2，否则转步4。
步4（分枝）：如果 $L^s=\empty$ ，转步1，否则，从 $L^s$ 选择节点 $P(X_i))$ 。剖分 $X_i$
为若干子集 $L_i^s=\{X_i^1,\cdots,X_i^p\}$ 并在 $L^s$ 中用 $L^s_i$ 对应的子问题替换 $P(X_i))$ 。令
$L:=L\cup L^s$ 。转步1。
步5（剪枝）：从 $L^s$ 中删除 $P(X_i))$ 。若 $i < k$ ，令 $i := i + 1$ ，回到步2，否则转步4。