由于一些原因, 需要学习一下强化学习。用这篇博客来学习吧,
用的资料是李宏毅老师的强化学习课程。
深度强化学习(DRL)-李宏毅1-8课(全)_哔哩哔哩_bilibili
这篇文章的目的是看懂公式, 毕竟这是我的弱中弱。
强化学习一般就是 环境, 动作网络, 奖励三者的纠缠,
动作网络看到环境, 产生一个动作, 然后得到一个奖励。 然后我们通过这个奖励来更新动作。
不同的方法有不同的思想, 我们来看看PG和PPO。
PG是这样的思想。
有一个policy网络 ,就是actor。 输入是环境, 输出是策略。
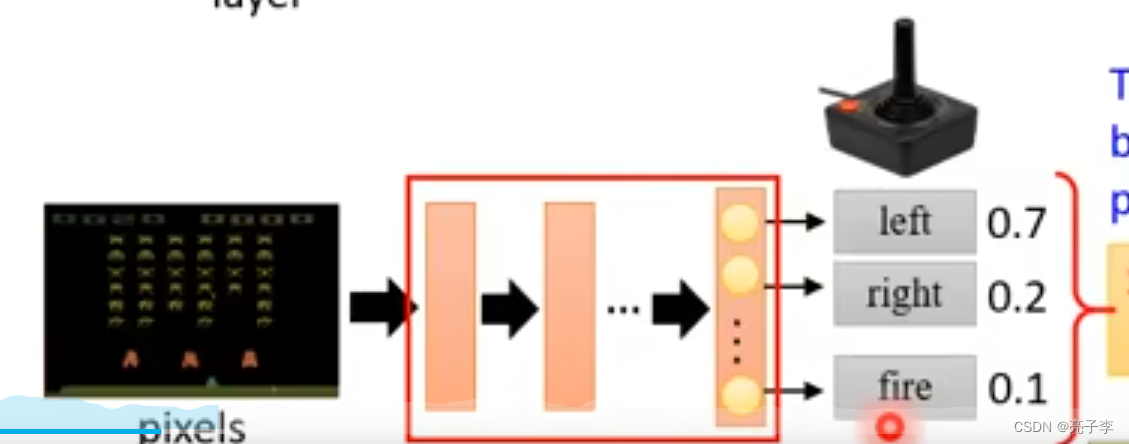
他会输出各个动作的几率, 然后可以根据这些几率采样一个动作。,
经过连续的一轮 也就是一个episode 就完成了一场游戏的采集。
将奖励加起来, 就是大R

我们的目标是让大R变得越大越好。
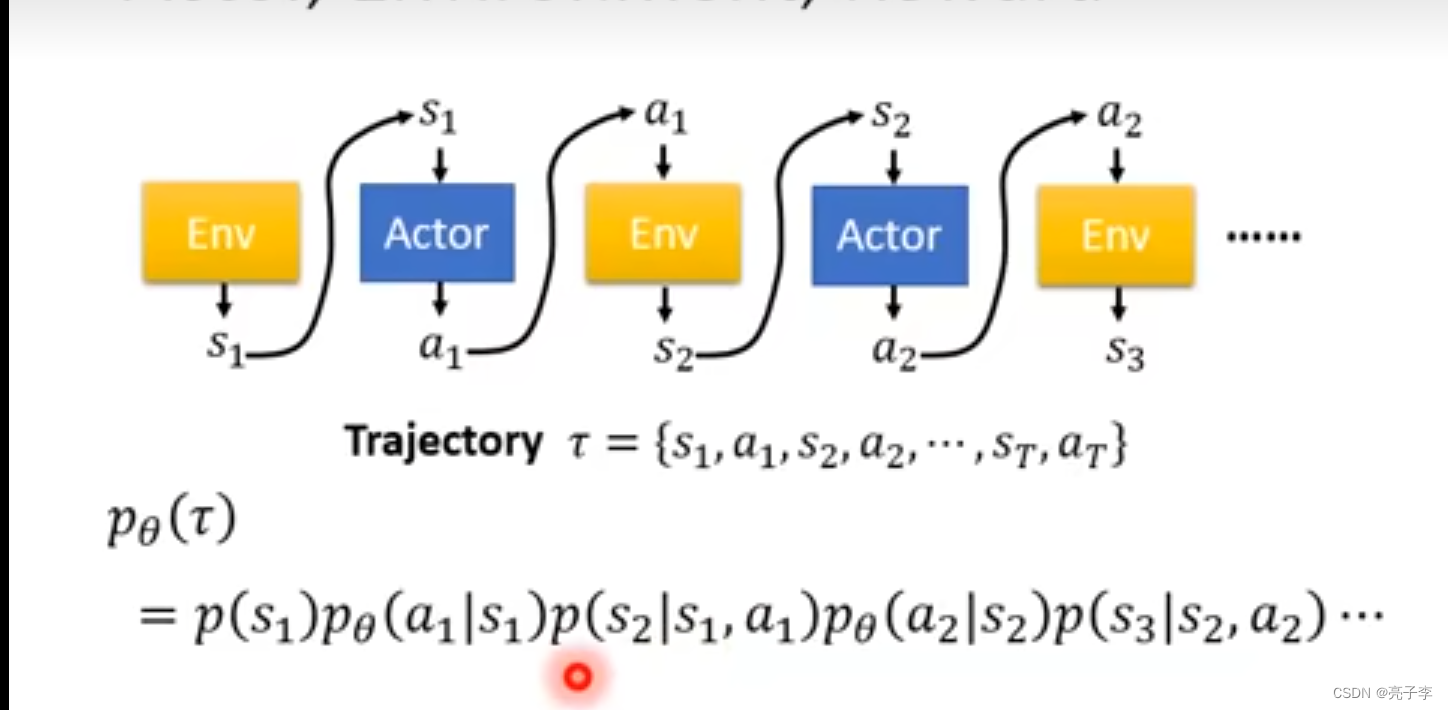
这是actor按照某个路线的概率。
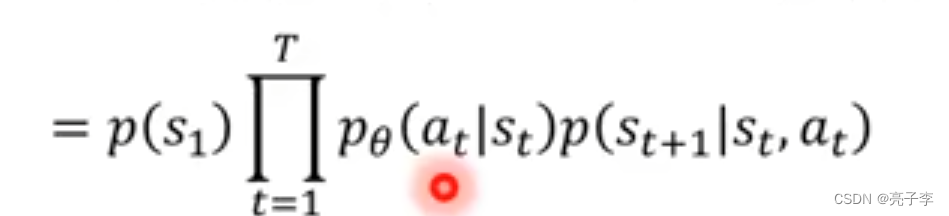
最后的组合概率。 也就是得到某一个结果的概率。
当然这条路线也会对应一个大R。

当然 对于同一个actor, 我们会进行很多个episode。 这样的话得到不同的路线
对应不同的奖励R() 乘加起来就是当前的actor 平均能得到的奖励了, 也就能评价当前actor的好坏。
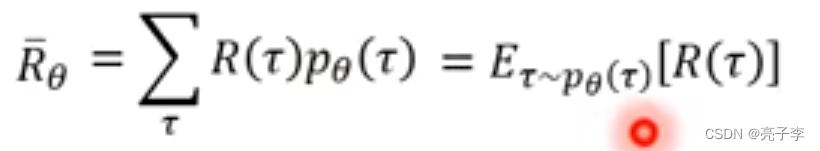
右边这种写法也是可以, 服从pxita这样的分布, 然后每个对应一个R, 得到一个期望,我们更新模型的目的就是让这个平均的R越大越好。
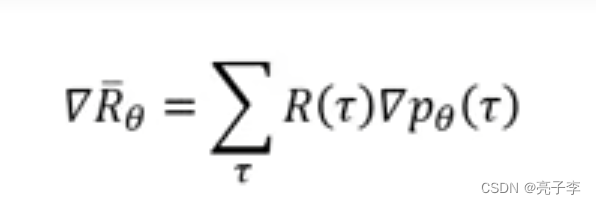
所以求R对参数的梯度,这里的R()不需要可微
由于右边只有与参数相关, 因此转化为对
的微分
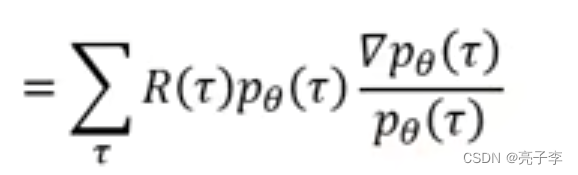
上下同乘(
)

变为这个。 因为对log求导 后面那一项。
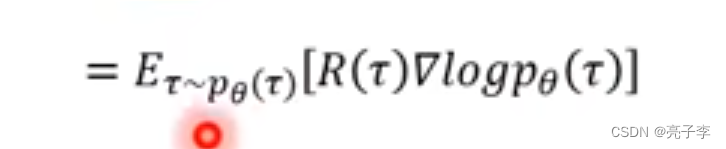
转为分布形式。

然后通过采样来模拟分布。
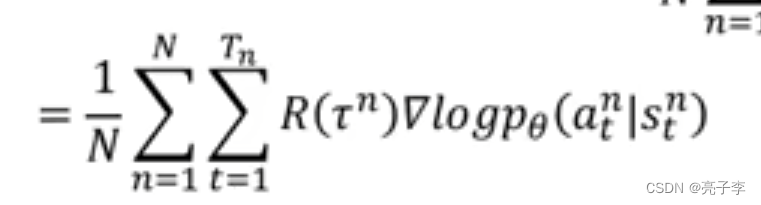
带入上面的(
)公式, 乘法就转为加法了。
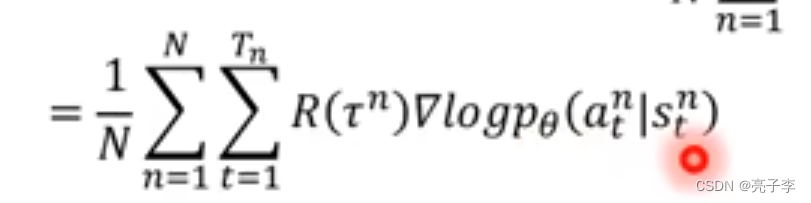
直观理解, 前面的R为正, 则增加后面这个S到A映射的几率, 通过更新模型参数。
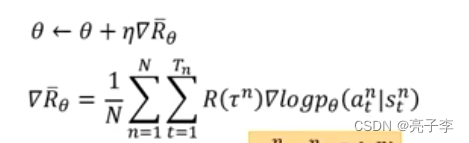
通过这两个式子, 我们就可以更新模型了。 问题是 第二个式子后面那一堆是从哪里来的呢?
事实上就是通过actor和环境互动得来的。 我们一直玩actor,得到很多个结果。
actor的操作一般是从softmax里采样出来的。
然后求softmax结果对参数的梯度, 然后乘上奖励就可以了。
我们会发现 这个R() 是对一个episode里所有sample的动作都起作用,
也就是说, 只要这一轮游戏的奖励是好的, 在这场游戏里所有做过的动作都会增加概率。
所以加上时间t, 只计算动作后面的奖励分数。

然后乘上一个discount。 discount 预示了一个动作的有效时间, 比如, discount很大的时候, 一个动作可以考虑非常多的步的奖励。
现在学了理论知识, 我们要实战通过代码来学习一下了。、
李宏毅HW12
首先是李宏毅老师的HW12。 助教放的代码, 我猜测是PG方法, 我们看下。
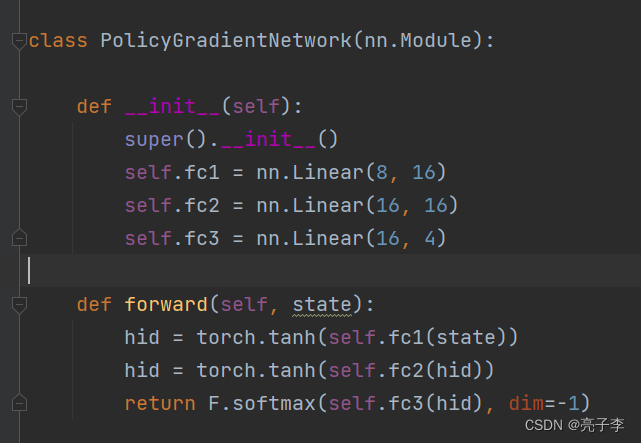
声明了一个网络,来产生策略。 输入是8维向量, 因为环境给出的接口是8维向量。
输出是4维向量, 因为可能的操作有4种。 可以看到最后还经过了softmax。
![]()
agent是模型的代理, 里面定义了模型的训练,保存等功能。

理论运行五轮游戏, 也就是五个episode。

等下看看这俩。
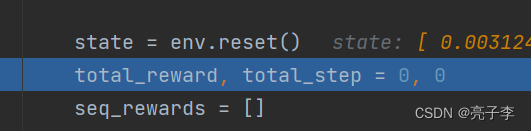
环境重置, 然后步数也都重置。

对于当前的环境state, sample一个动作。
![]()
action_prob是四个动作的几率。

categorical : 按类别赋值。 这里按照概率赋值, 之后就可以按概率来采样。

采样到了动作1.

这里的log_Prob是对action的概率取对数, 以e为底。
因为action1的概率为0.2368 因此取对数prob为-1.4404

把这一步输入进环境, 得到下一个环境的状态, 这一步的奖励, 和是否为最后一个动作。

这个注释已经解释了, 我们就是这样得到了每一对动作的概率值的对数。

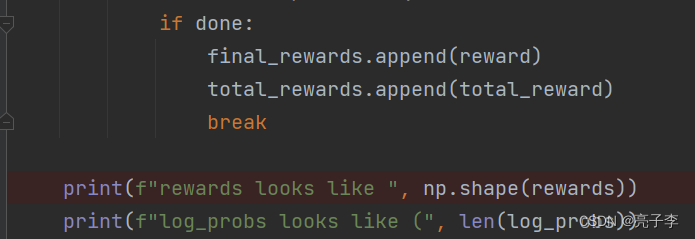
会记录每一步的reward 和 每一个eposide的reward和, 还会记录最后一步的reward。

对最后一步的reward和总rewarrd求平均。
![]()
将每一步的reward 归一化。
![]()
传入那个操作的概率对数和每一步的奖励, 更新模型。 我们看看。

因为loss要向小优化, 所以这里前面加了负号。 最后求和。
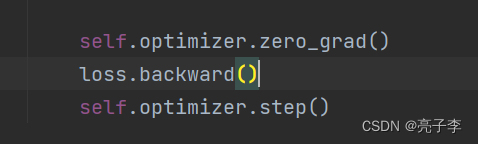
更新模型, 回传梯度。
这里可以看出 和公式是一模一样的。
我们参考的第二个代码来自于蘑菇书。 这本书一样
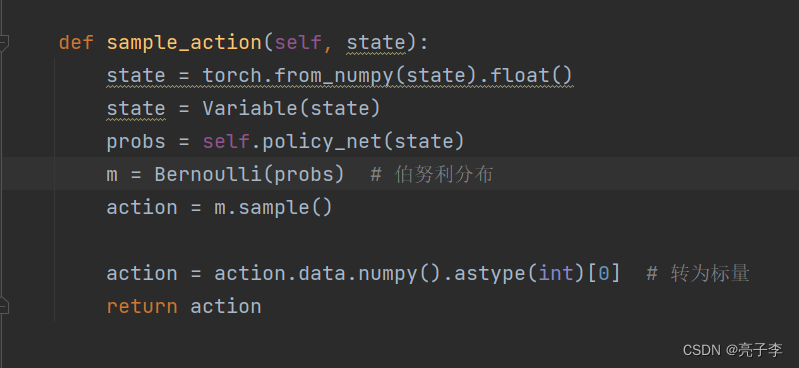
在sample 也是从分布中采样, 上面用的是softmax, 这里是伯努利。
state_pool, action_pool, reward_pool = self.memory.sample()
state_pool, action_pool, reward_pool = list(state_pool), list(action_pool), list(reward_pool)
# Discount reward
running_add = 0
for i in reversed(range(len(reward_pool))):
if reward_pool[i] == 0:
running_add = 0
else:
running_add = running_add * self.gamma + reward_pool[i]
reward_pool[i] = running_add
# Normalize reward
reward_mean = np.mean(reward_pool)
reward_std = np.std(reward_pool)
for i in range(len(reward_pool)):
reward_pool[i] = (reward_pool[i] - reward_mean) / reward_std
# Gradient Desent
self.optimizer.zero_grad()
for i in range(len(reward_pool)):
state = state_pool[i]
action = Variable(torch.FloatTensor([action_pool[i]]))
reward = reward_pool[i]
state = Variable(torch.from_numpy(state).float())
probs = self.policy_net(state)
m = Bernoulli(probs)
loss = -m.log_prob(action) * reward # Negtive score function x reward
# print(loss)
loss.backward()
self.optimizer.step()
self.memory.clear()这事更新模型的代码。
第一步, 先采样一组action结果。应该是一个 的一组结果(一个episode)
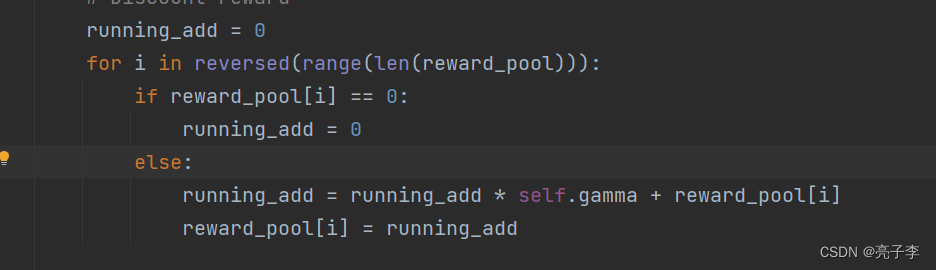
这里是乘以那个时间参数γ。 从后往前乘, 越向后乘的越多。

归一化。

和上面一样, 也是对action的概率取对数, 乘以reward。 但是伯努利的sample 的action是两个值。 不知道为什么。
不管怎么样, 我们大概知道PG的做法了。 就是算出来各个操作的概率, 然后放在一个分布里sample。 然后要对sample出来的操作的概率取对数 然后乘上它的奖励。 乘以一个负号, 最小化它。
代码在这里 :
https://github.com/datawhalechina/easy-rl/blob/master/notebooks/PolicyGradient.ipynb
https://colab.research.google.com/github/ga642381/ML2021-Spring/blob/main/HW12/HW12_ZH.ipynb#scrollTo=bIbp82sljvAt