1. 为什么要归一化

归一化（Normalization）是指将不同类型、不同取值范围等不同的数据按照一定的规则统一转化为相同的范围，使得数据在同一数值区间内比较、处理更加合理、有意义。归一化可以消除数据特征之间的量纲差异，使得每个特征在权重计算中起到相同的作用，同时还可以增加算法的收敛速度，提高模型的预测精度。

归一化的两种常用方法：

1. [0,1]归一化，使结果值映射到[0 ，1]之间。

$x^{*}=\frac{x - min}{max-min}$

2. 正态分布归一化，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1.

$x^{*}=\frac{x-\mu }{\delta }$ ,其中 $\mu$ 为均值， $\delta$ 为方差。

2. BN解决的问题：Internal Covariate Shift

我们知道网络一旦训练起来，那么参数就要发生更新，除了输入层的数据外(因为输入层数据，我们已经人为的为每个样本归一化)，后面网络每一层的输入数据分布是一直在发生变化的，因为在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例：网络的第二层输入，是由第一层的参数和input计算得到的，而第一层的参数在整个训练过程中一直在变化，因此必然会引起后面每一层输入数据分布的改变。（你可以理解为连锁反应）我们把在训练过程中，网络中间层数据分布的改变称之为：“Internal Covariate Shift”。BN的提出，就是要解决在训练过程中，中间层数据分布发生改变的情况，即Internal Covariate Shift问题。

3. 我们为什么需要BN？

我们知道网络一旦train起来，那么参数就要发生更新，除了输入层的数据外(因为输入层数据，我们已经人为的为每个样本归一化)，后面网络每一层的输入数据分布是一直在发生变化的，因为在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例：网络的第二层输入，是由第一层的参数和input计算得到的，而第一层的参数在整个训练过程中一直在变化，因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中，数据分布的改变称之为：“Internal Covariate Shift”。BN的提出，就是要解决在训练过程中，中间层数据分布发生改变的情况。

4. 理解BatchNormalization原理

一个标准的归一化步骤就是减均值除方差，那这种归一化操作有什么作用呢？我们观察下图

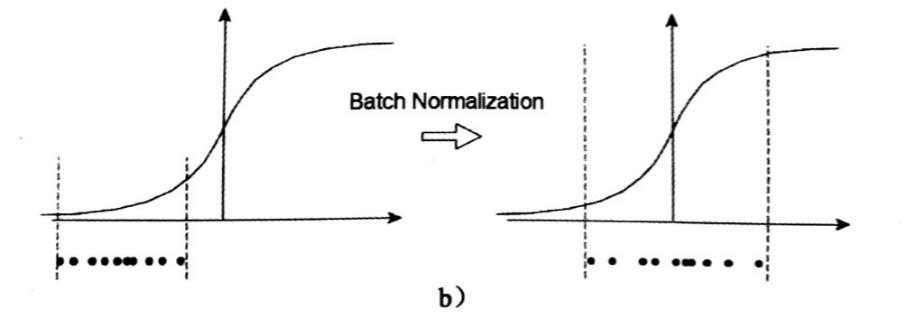
a中左图是没有经过任何处理的输入数据，曲线是sigmoid函数，如果数据在梯度很小的区域，那么学习率就会很慢甚至陷入长时间的停滞。减均值除方差后，数据就被移到中心区域如右图所示，对于大多数激活函数而言，这个区域的梯度都是最大的或者是有梯度的（比如ReLU），这可以看做是一种对抗梯度消失的有效手段。对于一层如此，如果对于每一层数据都那么做的话，数据的分布总是在随着变化敏感的区域，相当于不用考虑数据分布变化了，这样训练起来更有效率。

那么为什么要有第4步，不是仅使用减均值除方差操作就能获得目的效果吗？我们思考一个问题，减均值除方差得到的分布是正态分布，我们能否认为正态分布就是最好或最能体现我们训练样本的特征分布呢？不能，比如数据本身就很不对称，或者激活函数未必是对方差为1的数据最好的效果，比如Sigmoid激活函数，在-1~1之间的梯度变化不大，那么非线性变换的作用就不能很好的体现，换言之就是，减均值除方差操作后可能会削弱网络的性能！针对该情况，在前面三步之后加入第4步完成真正的batch normalization。

BN的本质就是利用优化变一下方差大小和均值位置，使得新的分布更切合数据的真实分布，保证模型的非线性表达能力。BN的极端的情况就是这两个参数等于mini-batch的均值和方差，那么经过batch normalization之后的数据和输入完全一样，当然一般的情况是不同的。

5. BN怎么做？

算法过程：

沿着通道计算每个batch的均值u
沿着通道计算每个batch的方差σ^2
对x做归一化，x’=(x-u)/开根号(σ^2+ε)
加入缩放和平移变量γ和β ,归一化后的值，y=γx’+β
加入缩放平移变量的原因是：保证每一次数据经过归一化后还保留原有学习来的特征，同时又能完成归一化操作，加速训练。这两个参数是用来学习的参数。

import numpy as np
def Batchnorm(x, gamma, beta, bn_param):
    # x_shape:[B, C, H, W]
    running_mean = bn_param['running_mean']
    running_var = bn_param['running_var']
    results = 0.
    eps = 1e-5

    x_mean = np.mean(x, axis=(0, 2, 3), keepdims=True)
    x_var = np.var(x, axis=(0, 2, 3), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta

    # 因为在测试时是单个图片测试，这里保留训练时的均值和方差，用在后面测试时用
    running_mean = momentum * running_mean + (1 - momentum) * x_mean
    running_var = momentum * running_var + (1 - momentum) * x_var

    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return results, bn_param

用keras 的代码调用. BatchNormalization调用要在激活函数之前和每一层之后。

from keras.models import Sequential
from keras.layers import Dense, BatchNormalization, Activation

model = Sequential()
model.add(Dense(64, input_shape=(input_shape,)))  # Input layer
model.add(BatchNormalization())  # BatchNormalization layer
model.add(Activation('relu'))  # Activation function (ReLU in this case)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/847570.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！